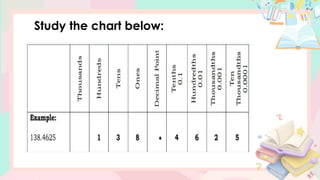
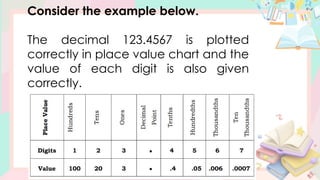
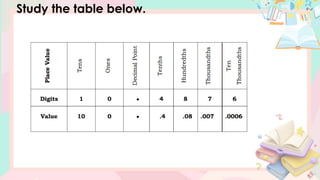
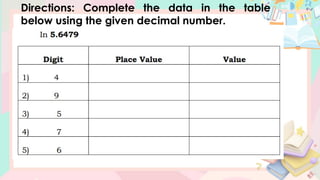
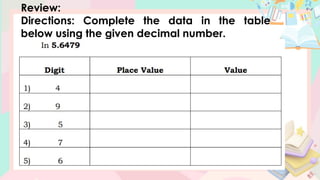
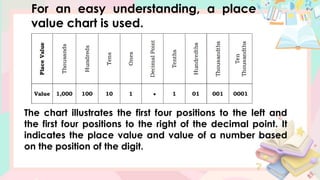
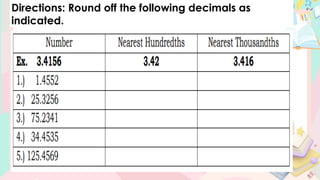
The document provides a comprehensive lesson on understanding and working with decimal numbers, focusing on place values, reading/writing decimals, and rounding them to specific positions. It includes examples, step-by-step instructions, and exercises related to identifying place values, reading decimal numbers aloud, and performing rounding operations. The content is structured for mathematics instruction for Grade 5 students over multiple days.

1. MATHEMATICS 5
QUARTER 1 WEEK 1
D
A
Y
1
PERIODICAL TEST

2. MATHEMATICS 5
QUARTER 1 WEEK 1
D
A
Y
2
PERIODICAL TEST

3. MATHEMATICS 5
QUARTER 2 WEEK 1
D
A
Y
3
Giving the Place Value and
the Value of a Digit of a
Given Decimal Number
through Ten Thousandths

4. Look at the numbers and try to read
each.
12.50
1.35
Do you know how to read
the following numbers?

5. Study the chart below:

6. Our lesson for today is all
about Giving the Place Value
and the Value of a Digit of a
Given Decimal Number through
Ten Thousandths

7. Consider the example below.
The decimal 123.4567 is plotted
correctly in place value chart and the
value of each digit is also given
correctly.

8. The place value is the position of
the digit in a number. It determines
the value that the number holds.
The value of a digit in a given
decimal is the product of that digit
holding the decimal place and the
value of that position.

9. Study the table below.

10. In 10.4876 the digit 0 is a place holder of
ones place. Its value is 0. Digit 1 is in the tens
place. Its value is 10. Digit 4 is in the tenths
place. Its value is 0.4. The digit 8 is in the
hundredths place. Its value is 0.08. The digit 7 is
in the thousandths place. Its value is 0.007. And
digit 6 is in the ten-thousandths place. Its value
is 0.0006. Hence, 10.4876 means ten and four
thousand eight hundred seventy-six ten
thousandths.

11. Directions: Complete the data in the table
below using the given decimal number.

12. Guess who and where I am: I am 178.3561.
a. I am the number 4th place from the left or 4th
number from the right.
a. Who and where am I? __________________
_____________________
b. I am located at the very end. Who and where
am I?
________________________________________
c. I am the 3rd number or the number before the
“and” in decimal form.
Who and where am I?
______________________________________

13. What is place value?
What is value of digit?

14. Multiple Choice. Write the letter of the correct
answer on a separate sheet of paper.

15. MATHEMATICS 5
QUARTER 2 WEEK 1
D
A
Y
4
Reading and Writing
Decimal Numbers

16. Review:
Directions: Complete the data in the table
below using the given decimal number.

17. Read the following numbers
below.
1,200 50.6
300 4000

18. To read, write and order
decimals properly, you need to
master what all the decimal
place values are. A place value
is the position of the digit in a
number. It determines the value
that the number holds.

19. For an easy understanding, a place
value chart is used.
The chart illustrates the first four positions to the left and
the first four positions to the right of the decimal point. It
indicates the place value and value of a number based
on the position of the digit.

20. Consider this example. Study and understand
this place value chart.
Based on the given chart, the digit 6 is in the tens place
while the digit 7 is in the thousandths place. Their values
would be 60 and 0.007, respectively.

21. Clearly, the place value chart helps you in giving
the place value and the value of a digit in a
decimal number.
Let us test your prior knowledge on giving the place
value and the value of a digit in a decimal number
by doing the exercise below.

22. How do you read 50.5880?
Here is the step-by-step process:
Step 1: Write the digits in the appropriate
boxes of the place value chart.

23. Step 2: Read the number to the left of
the decimal place as whole number.
50 is read as fifty.
Step 3: Read the decimal point as
“and”.
50. is read as fifty and.
Step 4: Read the number to the right of
the decimal place as whole number.
5 880 is read as five thousand eight
hundred eighty.

24. Step 5: When you’re done reading the number
to the right of the decimal point, say the place
value of the last digit.
 In 5 880, the last digit is 0 and its place value
is ten thousandths. So, it will be read as five
thousand eight hundred eighty ten
thousandths.

25. Another Example:
How to read 16.3?
Therefore 16.3 will be read as Sixteen
and three tenths.
Remember:
Read the decimal point as “and”.

26. Another Example.
How to read 0.15?
 15 is read as fifteen
 In 15, the last digit is 5 and its place value is
hundredths. So, it will be read as fifteen
hundredths.

27. Therefore, the decimal number 0.15
will be read as fifteen hundredths.
Clearly, when the decimal has no
whole number part, you just say the
decimal name.

28. Directions: Write the corresponding word form of
the following decimals. Follow the step-by-step
process. Step 1 of item number 1 is done for you.
12.0367
Step 1: Write the digits in the appropriate boxes of
the place value chart.

29. 12 is read as twelve
12. is read as twelve and
0367 read as three hundred sixty seven
0367 read as three hundred sixty seven
ten thousandths

30. Therefore, the decimal
number 12.0367 will be read
as:
_____________________________
_____________________________
_______.
Twelve and three hundred sixty
seven ten thousandths.

31. Read the following numbers below:
12.567
.98
135.7897

32. How to read decimal numbers?
In reading Decimal points, we follow the steps:
Step 1: Write the digits in the appropriate boxes of
the place value chart.
Step 2: Read the number to the left of the
decimal place as whole number.
Step 3: Read the decimal point as “and”.
Step 4: Read the number to the right of the
decimal place as whole number.
Step 5: When you’re done reading the number to
the right of the decimal point, say the place value
of the last digit.

33. Directions: Match each decimal number in Column A by writing the
letter that corresponds to the appropriate word forms in Column B. Write
your answers on your notebook.

34. MATHEMATICS 5
QUARTER 2 WEEK 1
D
A
Y
5
Rounding Decimal
Numbers

35. Review:
Directions: Match each decimal number in Column A by writing the
letter that corresponds to the appropriate word forms in Column B.

36. Read the situation below.
Javier is a Grade 5 student of Imus District. Every
day, he walks a distance of 10.7415 meters in
going to school from his house.
To the nearest hundredths, how far does Javier
walk every day from his house to the school?
To the nearest thousandths, how far is this?

37. The problem situation
above calls for rounding off
decimal numbers to the
nearest hundredths and
thousandths. For further
understanding about this
lesson, a step-by-step process.

38. To answer the problem, we used the number
line below to guide you for better
understanding on how to round off decimal
numbers.

39. Since 10.7415 is closer to 10.74
than 10.75, the decimal 10.7415
rounded to the nearest hundredths
is 10.74. In this case, we would say
that the decimal is rounded off to
10.74.

40. Notice that the given decimal 10.7415
is exactly halfway between 10.741 and
10.742. We round it off to 10.742. In this
case, we would say that the decimal is
rounded off to 10.742.

41. The following steps and examples are to be
considered in rounding off decimal numbers.
To round off decimal numbers:
1) Find the rounding digit occupying the
place value you’re rounding to. Then look
at the digit to the right of the rounding
digit.
2) If the number right after the rounding
digit is less than 5 (4, 3, 2, 1, 0), you have
to round down. This is done by leaving the
last decimal place as it is given and
discarding all the digits to its right.

42. In 10.7415
Think: 1<5. Therefore, you have to
round down. Then, drop all digits after
the rounding place.
Nearest hundredths:
Answer: 10.74

43. 3) If the number right after the rounding
digit is greater than or equal to 5 (5, 6, 7,
8, 9), you have to round up or add 1 to
the rounded digit and drop all the digits
to its right.
Nearest thousandths:

44. Think: 5 = 5
Therefore, you have to round up.
Then, add 1 to the rounded digit
and drop all the digits to its right.
Answer: 10.742

45. A. Round each decimal to the nearest
hundredths.
1) 51.732 = _____
2) 37.596 = _____
3) 30.361 = _____
B. Round each decimal to the nearest
thousandths.
4) 12.6458 = _______
5) 46.2143 = _______
51.73
37.60
30.36
12.646
46.214

46. If the number right after the
rounding digit is less than 5 (4, 3, 2,
1, 0), you have to _________. This is
done by leaving the last decimal
place as it is given and discarding
all the digits to its right.
Round Down

47. How to round off numbers?
If the number right after the
rounding digit is less than 5 (4, 3, 2,
1, 0), you have to _________. This is
done by leaving the last decimal
place as it is given and discarding
all the digits to its right.
Round Down

48. 2) If the number right after the
rounding digit is greater than or
equal to 5 (5, 6, 7, 8, 9), you have
to _________or add 1 to the
rounded digit and drop all the
digits to its right.
Round up

49. Directions: Round off the following decimals as
indicated.

50. MATHEMATICS 5
QUARTER 2 WEEK 1
D
A
Y
5
Catch-Up Friday