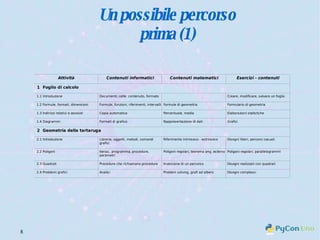
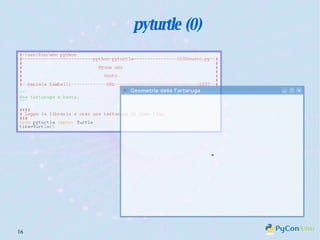
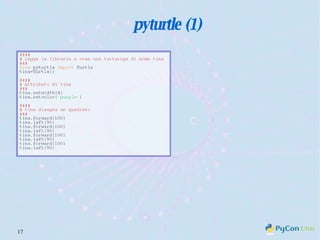
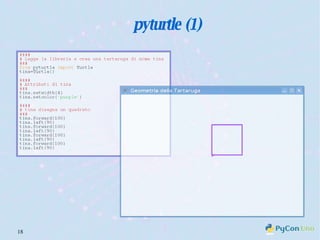
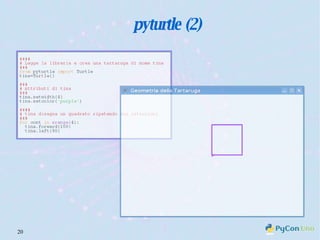
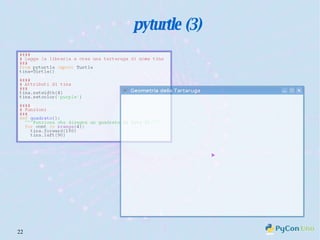
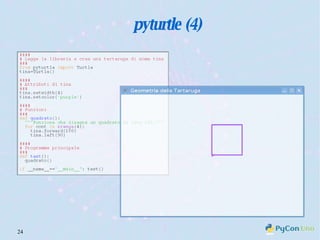
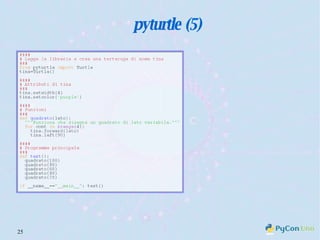
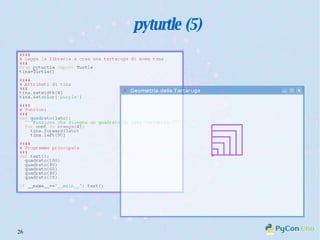
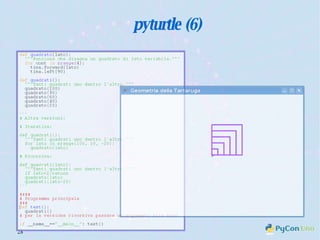
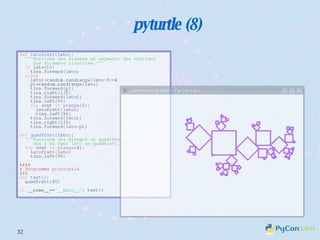
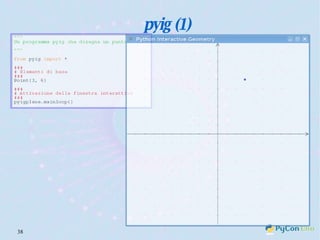
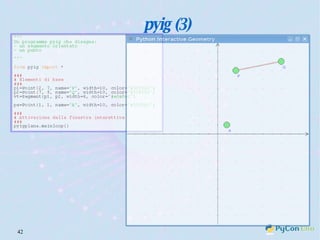
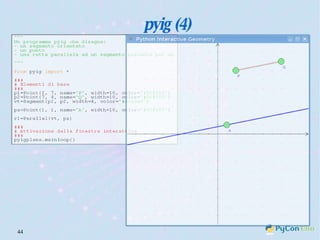
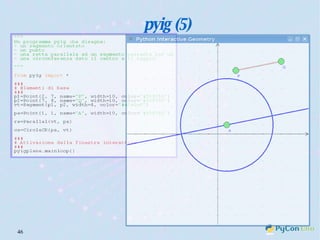
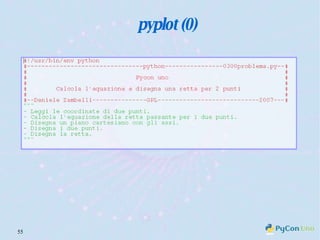
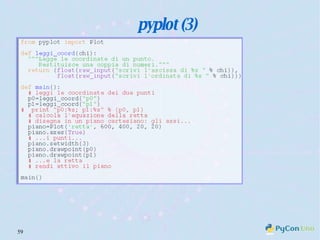
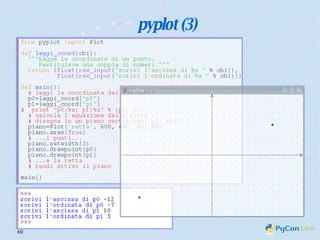
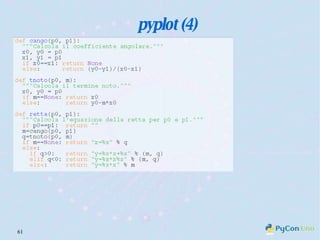
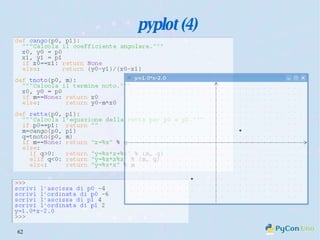
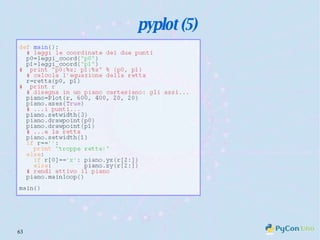
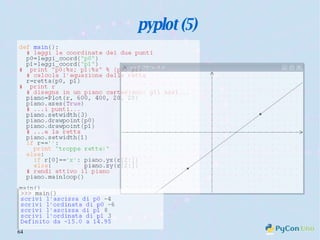
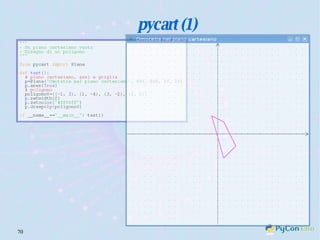
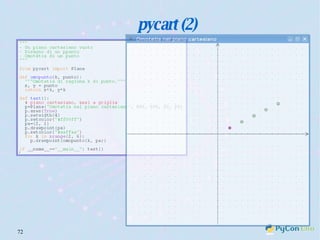
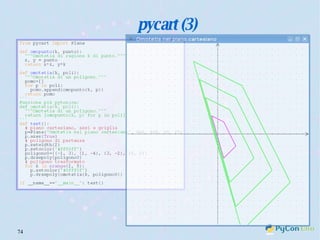
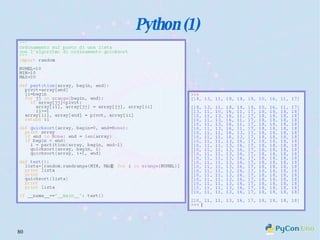
Il documento descrive l'uso di Python nell'insegnamento della matematica nelle scuole superiori, evidenziando i vantaggi del linguaggio per affrontare problemi matematici e il suo potenziale educativo. Vengono presentate librerie come pyturtle, pyig e pyplot, che offrono strumenti per esplorare concetti geometrici e grafici mediante programmazione. Infine, si sottolinea l'importanza della documentazione disponibile per supportare gli insegnanti e gli studenti nell'apprendimento di Python.