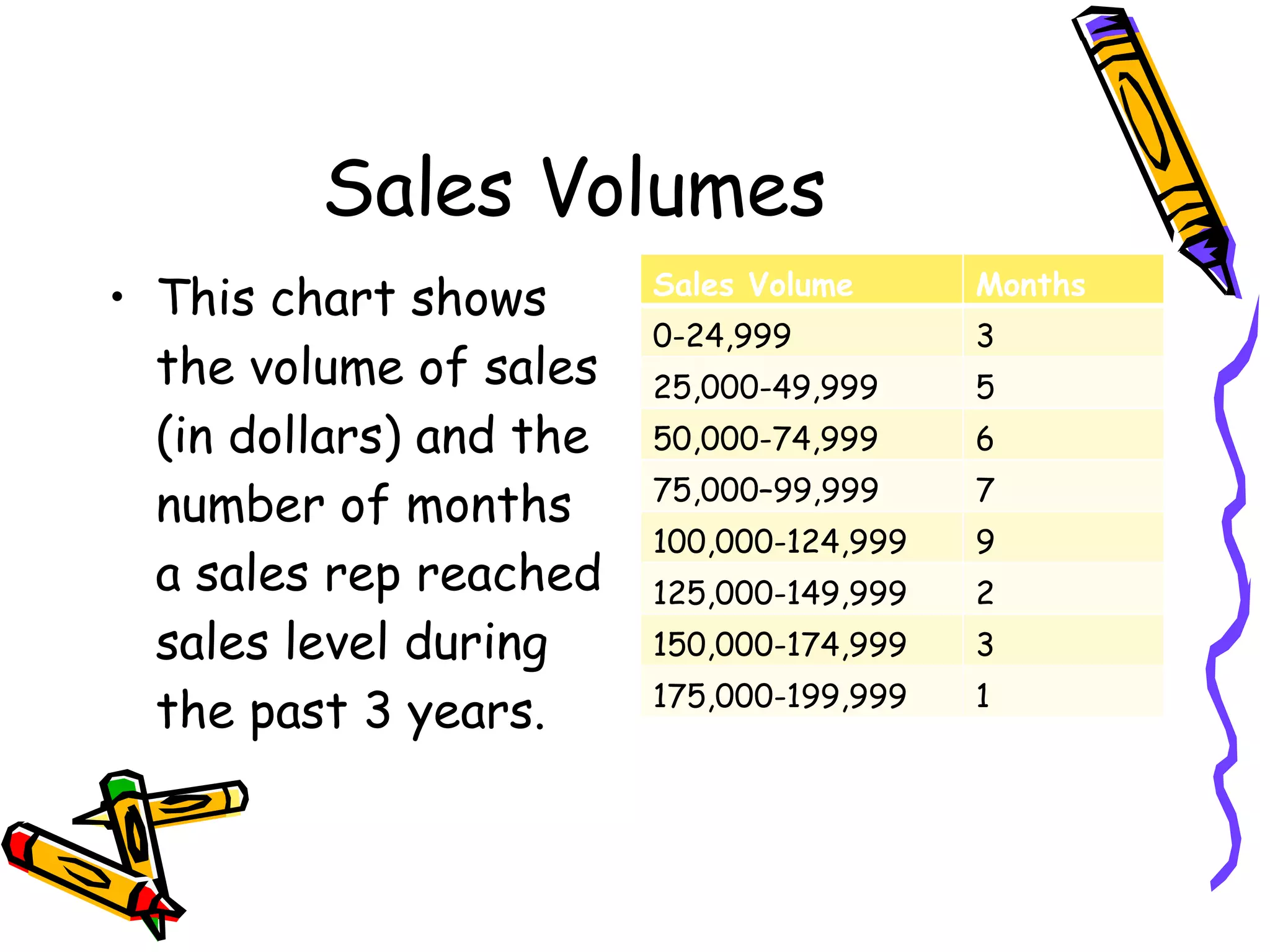
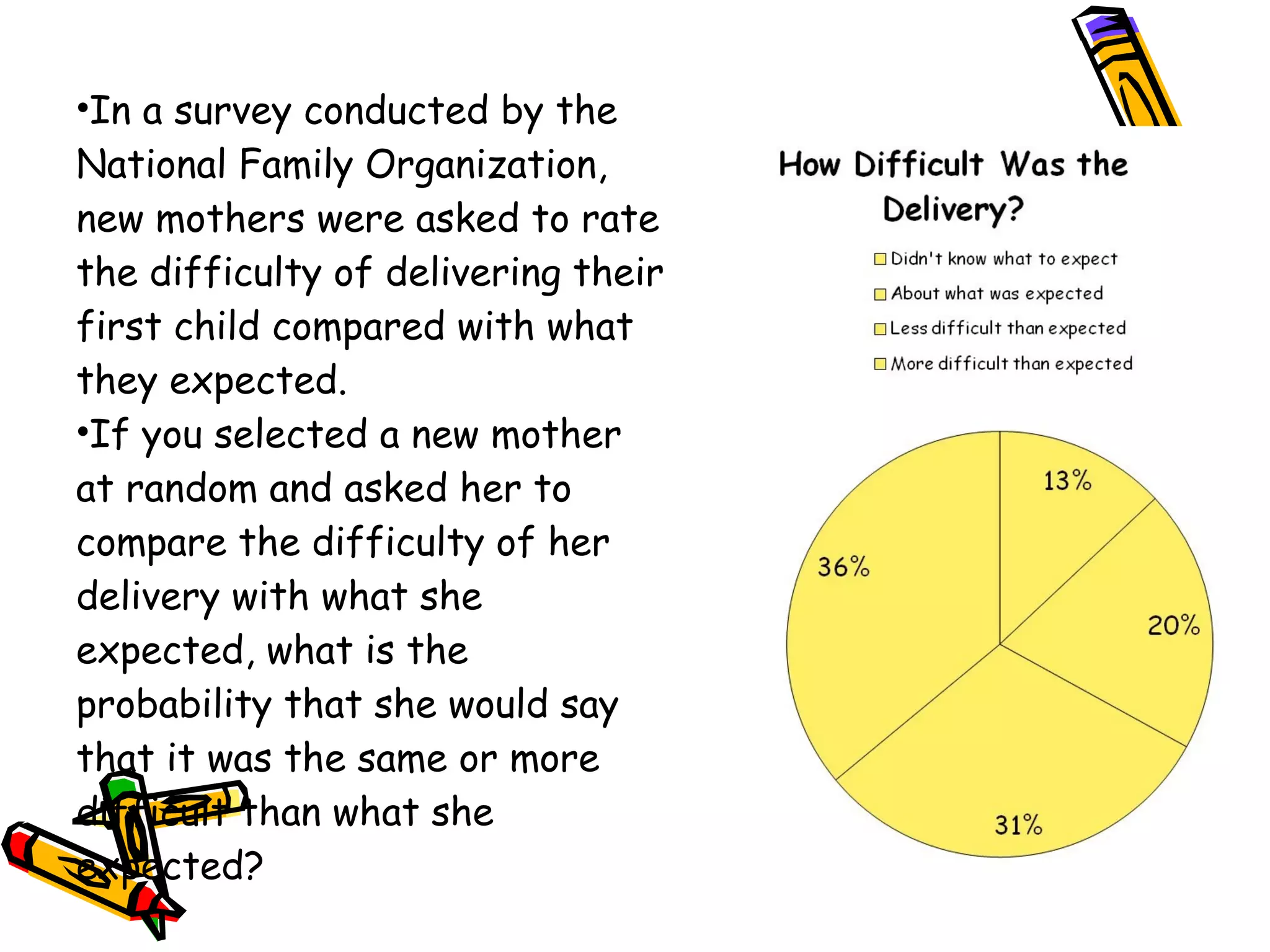
The document discusses probability and the addition rule. It provides examples of using the addition rule to calculate the probability of events occurring together or separately. It also includes examples calculating probabilities using data from surveys and draft pick statistics.

1. The Addition Rule Chapter 3.3

2. Objectives Determine if 2 events are mutually exclusive Use the Addition Rule to find the probability of 2 events

3. Mutually Exclusive Events Two events are mutually exclusive if A and B cannot occur at the same time. A A B B

4. Are these events mutually exclusive? Event A: Roll a 3 on a die Event B: Roll a 4 on a die yes

5. Are these events mutually exclusive? Event A: Randomly select a male student Event B: Randomly select an Auto Tech student No, a student can be both male and in Auto Tech

6. Are these events mutually exclusive? Event A: Randomly select a blood donor with type O blood. Event B: Randomly select a female blood donor No, a blood donor can be both female and type O

7. What is the probability of rolling a 3 or a 4 on a 6-sided die?

8. The Addition Rule The probability that events A or B will occur P(A or B) is given by P(A or B) = P(A) + P(B) – P(A-B) If events A and B are mutually exclusive, then the rule can be simplified to P(A or B) = P(A) + P(B)

9. Find the probability . . . Of selecting a card from a standard deck that is a 4 or an ace . . . P(4 or ace) = P(4) + P(ace) = 4/52 + 4/52 = 8/52 = 2/13 = .154

10. Find the probability . . . Of rolling a number less than 3 or an odd number . . . These events are not mutually exclusive P(less than 3 or odd) = P(less than 3) + P(odd) – P(less than 3 and odd) = 2/6 + 3/6 – 1/6 = 4/6 = 2/3 = .667

11. Sales Volumes This chart shows the volume of sales (in dollars) and the number of months a sales rep reached sales level during the past 3 years. Sales Volume Months 0-24,999 3 25,000-49,999 5 50,000-74,999 6 75,000–99,999 7 100,000-124,999 9 125,000-149,999 2 150,000-174,999 3 175,000-199,999 1

12. Sales Volumes If this sales pattern continues, what is the probability that the sales rep will sell between $75,000 and $124,999 next month? Sales Volume Months 0-24,999 3 25,000-49,999 5 50,000-74,999 6 75,000–99,999 7 100,000-124,999 9 125,000-149,999 2 150,000-174,999 3 175,000-199,999 1

13. Sales Volumes A = sales between 75,000 & 99,999 B = sales between 100,000 & 124,999 P(A or B)=P(A)+P(B) = 7/36 + 9/36 =16/36 =4/9 =.444 Sales Volume Months 0-24,999 3 25,000-49,999 5 50,000-74,999 6 75,000–99,999 7 100,000-124,999 9 125,000-149,999 2 150,000-174,999 3 175,000-199,999 1

14. In a survey conducted by the National Family Organization, new mothers were asked to rate the difficulty of delivering their first child compared with what they expected. If you selected a new mother at random and asked her to compare the difficulty of her delivery with what she expected, what is the probability that she would say that it was the same or more difficult than what she expected?

15. Example 5, p. 144 Use the graph on p. 144 to find the probability that a randomly selected draft pick is not a running back or a wide receiver. Define A: Draft pick = running back Define B: Draft pick = wide receiver P(A or B) =19/255 + 32/255 =51/255 = 1/5 P(not RB or WR) = 1 – 1/5 = 4/5 = .8

16. Turn to page 145 Do questions 1-9, 19 together Homework: 10-24 evens