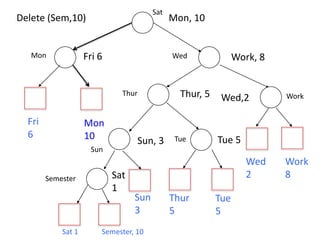
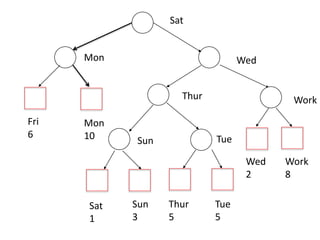
This document discusses priority search trees, which are binary search trees that also satisfy the priority queue property. It provides an example dataset with days of the week and priorities. It then shows how to build a priority search tree from an external binary search tree by associating keys with nodes and ensuring the tree forms a max heap. It describes operations like searching, insertion, deletion, and rebalancing the tree through rotations while maintaining both the binary search tree and priority queue properties.

1. Priority search trees, take 2

2. Data set for example
• Days of week with priorities: (Mon, 10), (Tues,
5), (Wed, 2), (Thur, 5), (Fri, 6) , (Sat, 1), (Sun,
3), (Work, 8).
• First, let’s look at one external binary search
tree formed from the keys.
– Internal nodes hold mid-range seperators and
pointers to left and right subtree
– Leaf nodes (external nodes), contain keys and
pointers to associated records.

3. Sat
Mon Wed
Fri
6
Mon
10
Thur Work
Sun Tue
Sat
1
Sun
3
Thur
5
Tue
5
Wed
2
Work
8

4. Building the priority search tree from
the external binary search tree
• Notice that our external tree is not a complete
binary tree like the example used previously for
points.
• Now, we relax the constraint that the tree be
external by associating each key with some node
on the path from its corresponding external node
to the root.
• Note we cannot associate all leaves with internal
nodes because there are not enough internal
nodes

5. Building the priority search tree from
the external binary search tree
• We additionally want the priorities of the
nodes to form a max heap.
• Can achieve this by playing a tournament
starting at the leaves, matches played
between siblings: winner of each match is the
one with higher priority, or the left son if there
is a tie.

6. Mon, 10
Fri
6
Mon
10
Work, 8
Sun, 3 Thur, 5
Sat
1
Sun
3
Thur
5
Tue
5
Wed
2
Work
8

7. Mon, 10
Fri
6
Mon
10 Sun, 3 Thur, 5
Sat
1
Sun
3
Thur
5
Tue
5
Wed
2
Work
8
Thur, 5
Work, 8

8. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue
5
Wed
2
Work
8
Thur, 5
Work, 8
Mon, 10

9. Building the priority search tree from
the external binary search tree
• Not exactly what we want, because there are
gaps between filled in nodes and the leaves.
• Fix this by bubbling up records to fill the gaps.
• The resulting tree is both
– A search tree for the keys and
– A max priority tree for the priorities

10. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Work, 8
Mon, 10
Fri 6
Wed 2
Tue
5

11. Using the priority search tree
• Basic query is to find all keys in the range
[lower, upper] whose priority is at least p
– This is just our familiar semi-infinite range query,
where we searched for all points with x
coordinates between x1 and x2 (so the x
coordinates were the keys) and y coordinate
greater than yp.
– Find all keys in the range [holiday, weekend] with
priorities at least 6

12. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Work, 8
Mon, 10
Fri 6
Wed 2
Tue
5
[holidays, weekend], 6
Sat
Mon Wed
Thur Work
Sun
Tue

13. Insertion
• We want to insert (K,p). K is the key used in the
BST and p is the priority.
• Whenever we insert a node into an “external”
BST it goes into a new external node, and one
new internal node is created.
• Two phases to insertion – one deals with the BST
side of things, and the other the max heap.
• Start by searching for K, which will take us to an
external node.

14. Insertion
• Specifically, insert (Semester, 10).
• Search gets down to the external node holding
Saturday.
• Create a new internal node – it will have two
sons: Saturday to the left and Semester to the
right.
– The mid-range separator is Semester
– Promote (Sat, 1) to the new internal node, if it was
not previously promoted

15. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Work, 8
Mon, 10
Fri 6
Wed 2
Tue
5
Sat
Mon Wed
Thur Work
Sun
Tue
Semester
Semester, 10
Sat 1

16. General situation – insert K’, p’
K
(K,n)
K’ K,n
K’
K
K’ K,n
K
K’
K
or
K’ > K K’<=K

17. Second stage of insertion
• Retrace the path from the insertion point to
the root until encountering a node with
priority higher than the insertion point
– We might get to the root and never find such a
point.
K,p
L,m
K’,p’
K,p
K’,p’
m > p’ > p p’ >p

18. Second stage of insertion
• Now, we replace (K,p) with (K’,p’) and bubble
(K,p) down the tree.
• Make sure to bubble down the correct path to
maintain the BST property!
– In a regular heap it does not matter which branch
you bubble down, but in a priority search tree it
does.
• In our example, (K,p) = (Work, 8)

19. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Semester,10
Mon, 10
Fri 6
Work,8
Tue
5
Sat
Mon Wed
Thur Work
Sun
Tue
Semester
Semester, 10
Sat 1

20. Deletion
• Two deletion operations:
– DeleteP – delete the record with largest priority –
really just like heaps
– DeleteK – delete record with key K.
• DeleteK has two phases: a search tree phrase
and a priority tree phase.
– Deletion will remove the external node associated
with the key, and so will also reduce by one the
number of internal nodes.

21. Deletion
• Star by finding the node holding the record
(K’,p’)
– This can be an internal node if (K’, p’) was bubbled
up after insertion
– Or it can be an external node
• Remove (K’, p’) from that node and bubble up
a record to fill the gap.
– If (K’, p’) were in an external node or the root of a
subtree with no records in the subtree, then there
is no need to bubble up.

22. Deletion
• Now we want to delete the external node
associated with (K’,p’).
– Remove the external node and its parent, and then
connect the sibling of the deleted external node to its
grandparent.
– If the parent was associated with (K,p) we trickle it
down the tree.
K’
K, p
K, p

23. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Semester,10
Mon, 10
Fri 6
Work,8
Tue
5
Sat
Mon Wed
Thur Work
Sun
Tue
Semester
Semester, 10
Sat 1
Delete (Sem,10)

24. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Work, 8
Mon, 10
Fri 6
Work,8
Tue
5
Sat
Mon Wed
Thur Work
Sun
Tue
Semester
Semester, 10
Sat 1
Delete (Sem,10)

25. Fri
6
Mon
10 Sun, 3
Sat
1
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Work, 8
Mon, 10
Fri 6
Wed,2
Tue
5
Sat
Mon Wed
Thur Work
Sun
Tue
Semester
Semester, 10
Sat 1
Delete (Sem,10)

26. Fri
6
Mon
10 Sun, 3
Sun
3
Thur
5
Tue 5
Wed
2
Work
8
Thur, 5
Work, 8
Mon, 10
Fri 6
Wed,2
Tue
5
Sat
Mon Wed
Thur Work
Sun
Tue
Sat 1
Delete (Sem,10)

27. Rebalancing
• Since the trees are dynamic, if we do not
rebalance through rotations they can become
narrow and deep.
• Treat them like AVL trees, and perform
rotations when balance factors leave their
allowable range.
• We’ll look at single rotations, sometimes
called “promotions” in the literature.

28. Promotions – BST part
Promote v
(K,p)
3
2
1
v
v
3
2
1
(L,q)
u
u (L,q)
(K,p)
Promote u

29. Promote v (right rotation)
• BST properties are preserved
• But priority search condition not necessarily
preserved:
– All records in subtrees 1,2,3 have priority no
greater than q
– All records in subtrees 1,2 have priorities no
greater than p
– So we had better switch (K,p) and (L,q) – these are
NOT the mid-range separators, but the records
and priorities associated with those nodes!

30. Promote v (Priority part)
3
2
1
(L,q)
u
3
2
1
(L,q)
u
(K,p)
v
v
(K,p)

31. Promote v (Priority part)
• Because p <- q, nodes u,v, and subtrees 1 and
2 satisfy the priority search tree condition.
• But subtree 3 may not.
– Solved by tricking (K,p) down that subtree, which
will take time proportional to the height of the
priority search tree.
– And we are done!