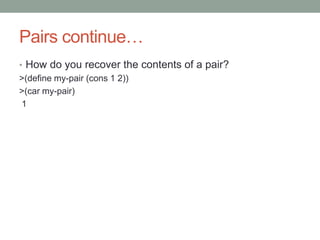
Scheme is a functional programming language developed in the 1970s at MIT. It is influenced by Lisp and has influenced languages like JavaScript, Ruby, and Clojure. Scheme uses s-expressions and supports both Windows and Linux. It is commonly used for embedded systems, compiler design, scripting, and teaching at many universities. The language has variants like Chez Scheme and Chicken Scheme. Core elements of Scheme include procedures, recursion, lambda expressions, conditionals, boolean logic, pairs, lists, vectors, and arithmetic operations.

1. SCHEME LANGUAGE
Jitendra Lenka
Sr. Software Engineer,
L&T Tech Services, Mysore

2. Introduction
• First appeared in 1975
• Functional programming language
• Scheme was developed at the MIT AI Lab by Guy L. Steele and
Gerald Jay Sussman
• Scheme is influenced by Lisp
• Scheme influenced Java Script, Ruby, Common Lisp
• Clojure, Common Lisp, Dylan, EuLisp, Haskell, Hop, JavaScript,
Kernel, Lua, R, Racket, Ruby
• s-expressions, parenthesized lists in which a prefix operator is
followed by its arguments.
• It supports both in Windows and Linux platform.

3. Introduction Continues…
• It uses small size interpreter
• Uses in embedded system, compiler design, scripting.
• Google App Inventor for Android uses Scheme, where Kawa is used
to compile the Scheme code down to byte-codes for the Java Virtual
Machine running on Android devices
• List of Universities teach Scheme :
• MIT
• Northeastern University and Worcester Polytechnic Institute
• Rice University, etc

4. Scheme Variant
• Chez Scheme
• Chicken Scheme
• Racket Scheme

5. First Program
>(sqrt 23)
4.79583152331272
>(display “Hello World”)
(newline)

6. Integer Arithmetic
(+ 100 200)
(+ 10 20 30 40 50 )
Q: What about negative number

7. Integer Procedures
• remainder
• quotient
• Max
• min

8. Nested Procedure Call
(* (- 7 3) (+ 5 12))
(* (quotient (* 7 41) (- (max 38 14) 35))

9. Definition
>(define freezing 32)
> (define boiling 212)
(- boiling freezing)
180
(define seconds-in-week (* 7 24 60 60))

10. Local & Global Binding
• Local
>(let ((number 5)) (* number (+ number 1)))
30
Question : What will be the output ?
> (+ 12 number)

11. Local & Global Binding
• Global Binding
>(define number 100)
>number
100
>(let ((number 5)) (* number (+ number 1)))
30
Q: What is output ?
> number

12. Internal Definition
(let ((number 5))
(define successor (+ number 1)) (* number
successor))

13. Simple Procedure
Definition :
> (define (square root) (* root root))
Calling ‘square’ procedure:
> (square 10)

14. Lambda Expression
• Lambda
(define disparity (lambda (a b) (abs (- a b))))
• Without Lambda
(define (disparity a b) (abs (- a b)))

15. Boolean Expression
>(not #f)
>(not #t)
>(not 5)
>(not not)

16. Boolean Expression Continues…
• So you use the boolean? predicate to distinguish Boolean
values from values of other types?
>(boolean? #t) #t
> (boolean? #f) #t
> (boolean? 0) #f
> (boolean? (lambda (augend) (+ augend 3))) #f
> (boolean? boolean?) #f
> (boolean? (boolean? boolean?)) #t

17. Compare Boolean expression
• >(eq? #t #t)

18. Equal and Inequality Procedure
• Equal
>(= 5 6)
• Inequality
(define (~= first-num second-num)
(not (= first-num second-num)))

19. Factorial Function
>(define (factorial n)
(if (zero? n)
1
(* (factorial (sub1 n)) n)))
>(factorial 0)

20. Pairs
• Pascal, in which procedures can return only simple data
values; but in Scheme a procedure can return anything
• If you have exactly two values to pack together, the best data
structure to use is a pair -- a container designed specifically to
hold two values. The two values packed into a pair are
completely independent of one another; they need not belong
to the same data type.

21. Pairs continue…
How do you construct a pair?
>(cons 1 2)
(1 . 2)
>(cons #t #f)
(#t . #f)
So a pair can be a component of another pair?
>(cons (cons 1 2) 3) ((1 . 2) . 3)
Q:What Will bé the output ?
(define lp (cons (cons (cons (cons (cons 1 2) 3) 4) 5) 6) )

22. Pairs continue…
• How do you recover the contents of a pair?
>(define my-pair (cons 1 2))
>(car my-pair)
1

23. List
Using list we can pack more than two values.
How does Scheme treat lists differently from other pairs in Scheme?
>(cons 1 (cons 2 '()))
(1 2)
use the shorthand notation for lists when you type them in, too?
>'(8 4 6 1)
(8 4 6 1)
>'()
()
Q: What will be the output
> (cons 1 (cons 2 (cons 3 4)))

24. List continues…
>(define list-of-six (list 6 5 4 3 2 1))
Empty List: null procedure defines it. which takes one argument and
determines whether its operand is the empty list and returns Boolean
value.
>(null? '()) #t
> (null? '(3)) #f
>(null? (cons 1 2)) #f
>(null? (cdr '(3))) #t
> (null? (cdr (cons 3 '()))) #t

25. List continues…
> (list 1 2 3 4) (1 2 3 4)
> (list (cons 1 2) (cons 3 4) (cons 5 6)) ((1 . 2) (3 . 4) (5 . 6))
> (list (+ 1 12) (* 60 4)) (13 240)
> (list 28) (28) > (list) ()
List-ref procédure : extract value from a list.
>(list-ref '(0 1 4 9 16 25 36 49 64 81 100 121) 7)
49

26. Vectors
• Vectors are heterogeneous structures whose elements are indexed
by integers. A vector typically occupies less space than a list of the
same length, and the average time required to access a randomly
chosen element is typically less for the vector than for the list.
> (define my-vec (vector 1 2 3))
> my-vec
#(1 2 3)
> (vector-ref my-vec 2)
3

27. Vector continues…
• Useful procedures
(vector obj)
Create a vector
(vector? Obj )
Returns boolean
(vector-length vector)
Returns the number of elements of the venctor.
Vector->list vector
(vector-list ‘#(12 13 14))
List->vector
(list->vector ‘(1 2 3))

28. THANK YOU