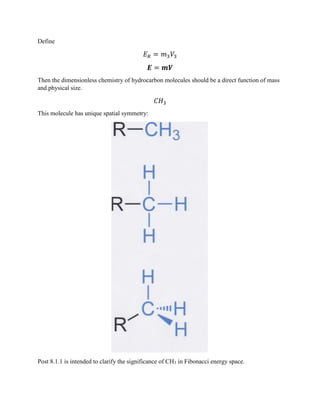
The document discusses number systems used in the physical and computational sciences and explores natural events in Fibonacci number space. It establishes definitions and relationships for natural logarithms, Planck's constant, gravitational acceleration, energy, and dimensional analysis using Fibonacci numbers. The post aims to clarify the significance of the CH3 molecule in relation to its unique spatial symmetry and position in Fibonacci energy space.

1. Number Systems
Background: Number Systems is a post to explore number systems in general and for use in the
physical and computational sciences.
Post 8.1
Natural Events in Fibonacci Number Space
Medical Sciences
Posts 1 – 8 have established:
1 𝐷 = (1 +
𝛾∞
𝑓
𝑇𝐷
)
−1
(1 +
𝛾 𝐷
𝑓
𝑇𝐷
)
+1
For natural events, this definition should correlate to the Bernoulli base of natural logarithms:
∫
1
𝑥
𝑑𝑥
𝑒
1
= 1 where lim
𝑛→∞
(1 +
1
𝑛
)
𝑛
= 𝑒
A mathematical description of nature should not be accurate unless the number system complies
with both natural conditions of the number one shown above.
Natural examples:
1
𝑐3
2 =
1
35
2 𝑥 10−16
meter-2 sec+2
h = 6.6260700 E-34 = 6.6260700 x (1∞ − 𝑅 𝐸
𝑓{3}
) x 10-34
meter+2 kg+1 sec-1
𝒘𝒉𝒆𝒓𝒆 𝒂 𝒈 = 𝒈
when g = gEarthSurface <g units: acceleration+1 second+2>
It has been shown
𝐸
𝐸 𝐵
= 𝑚𝑉𝐵
To be rigorous, energy can be defined as a ratio:
𝐸
𝐸 𝐵
= 𝑚𝑉𝐵
Kilogram+1 Meter+3

2. Define
𝐸 𝑅 = 𝑚3 𝑉3
𝑬 = 𝒎𝑽
Then the dimensionless chemistry of hydrocarbon molecules should be a direct function of mass
and physical size.
𝐶𝐻3
This molecule has unique spatial symmetry:
Post 8.1.1 is intended to clarify the significance of CH3 in Fibonacci energy space.