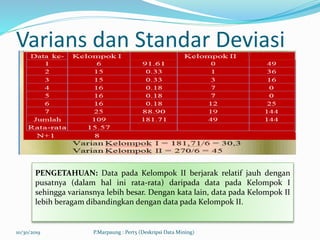
Dokumen ini membahas tentang deskripsi data mining, termasuk cara mendeskripsikan data tinggi badan siswa dengan metode grafis dan lokasi untuk memperoleh informasi yang lebih praktis. Terdapat penjelasan tentang median, modus, kuartil, dan ukuran keberagaman seperti varians dan standar deviasi untuk menggambarkan data secara lebih lengkap. Dengan pendekatan ini, peneliti dapat memberikan analisis yang lebih akurat terkait data yang ada.

1. 10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

2. Fungsi Deskripsi Pada DW
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
Sebagai gambaran, terdapat data tinggi badan para siswa dari kelas
yang tidak diberi makanan suplemen dan dari kelas yang diberi
makanan suplemen peninggi badan.

3. Fungsi Deskripsi
 Jika peneliti memutuskan untuk melibatkan 10000
siswa. Peneliti tersebut butuh melibatkan begitu
banyak orang agar hasil penelitiannya lebih dapat
dipercaya.
 Menelusuri deretan angka sebanyak itu dengan mata
manusia tentu tidak akan membawa manfaat apa pun
 Terdapat banyak cara untuk memberikan deskripsi
terhadap sekumpulan data.
1. Deskripsi grafis
2. Deskripsi lokasi
3. Deskripsi keragaman
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

4. 1. Deskripsi Grafis
 Cara deskripsi grafis merupakan cara untuk
mendeskripsikan data dalam bentuk gambar yang
sesungguhnya.
 Dua gambar yang umum digunakan dalam deskripsi grafis
adalah
 Diagram titik (dot diagram) dan
 Histogram.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

5. 1.1 Diagram titik
 Setiap data digambarkan sebagai sebuah titik (dot). Mengambil tabel
untuk kelas A dan B, setiap data tinggi badan Kelas A digambarkan
sebagai titik warna hitam, sementara Kelas B berupa titik warna
merah.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
 PENGETAHUAN: kelas A (titik penuh) banyak berkumpul di
sekitar 165-170 cm. Sementara kelas B (titik berongga) cenderung
berkumpul di atas 175 cm, namun nilainya beragram dengan
seberan yang lebih luas.

6. 1. 2. Histogram
 Misalnya, kita diberi data tinggi badan dari Kelas A yang telah
disajikan pada Tabel di bawah, namun kali ini data tersebut diperluas
hingga ada 30 siswa.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
Nomor Siswa Tinggi Nomor Siswa Tinggi Nomor Siswa Tinggi
Badan Badan Badan
1 168 11 169 21 167
2 164 12 167 22 166
3 167 13 169 23 165
4 164 14 167 24 166
5 171 15 164 25 169
6 166 16 166 26 171
7 169 17 168 27 166
8 172 18 167 28 167
9 166 19 165 29 164
10 166 20 164 30 165

7. 1. 2. Histogram
 Langkah pertama membuat histogram adalah membuat
beberapa interval yang lebarnya sama.
 Interval masing-masing dengan rentang 2 cm akan dibuat.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
Interval Interval Frekuensi
164-166 164-166 8
166-168 166-168 13
168-170 168-170 6
170-172 170-172 2
172-174 172-174 1
 Hitung seberapa banyak data yang menjadi anggota tiap
interval

8. 1. 2. Histogram
 pembuatan histogram itu sendiri berdasarkan data yang
direkap
PENGETAHUAN: dapat dilihat langsung di histogram.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

9. 2. Deskripsi lokasi
 Deskripsi grafis sudah menggambarkan karakteristik
data, sifatnya masih terlalu kasar dan kurang praktis
untuk dilakukan.
 Kita memerlukan sebuah angka yang cukup dapat
mewakili data yang ada serta dapat diperoleh dengan
cara yang lebih praktis daripada menggambar.
 Wakil tersebut dinamakan lokasi karena dapat
memberikan informasi tentang data dari posisi tertentu.
 Jenis-jenisnya: Mean, Median, Modus, Kuartil
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

10. 2. 1. Mean
 Sesuai dengan namanya, rata-rata berarti ‘membuat
menjadi rata’, dan nilai perataan tersebut dianggap sebagai
lokasi pusat, titik berat, atau titik kesetimbangan data.
 Secara matematis, bila nilai observasi x1,x2,…,xn, maka rata-
ratanya adalah :
 Secara sederhana, persamaan tersebut berarti menjumlahkan semua
data, kemudian dibagi dengan banyaknya data.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
 ( x1  x2 ....  xn) n x1
x 


n nt 1

11. 2. 1. Mean
Data Kelas A: 168, 164, 167, 164, 171, 166, 169, 172, 166, 166
Data Kelas B: 175, 176, 183, 180, 177, 177, 182, 179, 179, 171
 Apabila deret di atas dijumlahkan baik dari kelas A maupun dari kelas B,
maka jumlah total dari kelas A adalah 1673 sehingga rata-rata kelas A
adalah 1673/10= 167,3 cm.
 Sedangkan apabila kita menjumlahkan seluruh data Kelas A, hasil yang
diperoleh adalah 1779 sehingga rata-rata kelas A adalah 1779/10=177.9
cm.
PENGETAHUAN: Menggunakan bahasa sehari-hari, hasil di atas
menyatakan bahwa pada umumnya siswa Kelas A memiliki tinggi badan
167,3 cm.
Siswa kelas tersebut lebih pendek daripada siswa Kelas B yang pada
umumnya memiliki tinggi badan 177,9 cm.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

12. 2.2 MEDIAN
 Dengan ukuran ini, nilai observasi yang secara
harfiah “bertempat di tengah-tengah” dapat dicari.
 Langkah pertama adalah mengurutkan
semua data dari yang terkecil hingga yang
terbesar
- Data Kelas A: 168, 164, 167, 164, 171, 166, 169, 172, 166, 166
- Data terurut: 164, 164, 166, 166, 166, 167, 168, 169, 171, 172.
 Karena jumlah data adalah 10 buah data (genap), maka lokasi tengah
teletak diantara data ke-5 dan data ke-6.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

13. 2.2 MEDIAN
 Secara matematis, apabila terdapat n buah data, maka
mediannya telatak pada data ke-[(n+1)/2] apabila n
adalah bilangan ganjil. Sebaliknya apabila n adalah
bilangan genap, maka mediannya dihitung dengan cara
menjumlahkan data ke-[n/2] dengan data ke-[(n+1)/2],
kemudian membagi hasil jumlah tersebut dengan
angka 2.
 Median = [(data ke-5+data ke-6)/2]=[(166+167)/2]=166.5
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

14. 2.2 MEDIAN
 PENGETAHUAN: Apabila data kelas A diurutkan dari
yang terpendek sampai yang tertinggi, kemudian urutan
tersebut dapat dibagi dua tepat di tengah-tengah, dengan
nilai tengah 166.5.
 Keuntungan penggunaan median dibandingkan dengan
rata-rata adalah median tidak terlalu terpengaruh oleh
adanya nilai ekstrim . Sebaliknya, rata- rata dapat
terpengaruh oleh nilai ekstrem.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
Data terurut: 164, 164, 166, 166, 166, 167, 168, 169, 171, 172. (Rata-rata= 167.3, Median = 166.5)
Data terurut: 164, 164, 166, 166, 166, 167, 168, 169, 171, 1720. (Rata-rata= 332,1, Median = 166.5)

15. 2.3 MODUS
 Dengan ukuran ini, nilai observasi yang paling sering
muncul dapat dicari. Apabila terdapat dua atau lebih nilai
yang kekerapan munculnya sama, semua nilai-nilai
tersebut juga disebut modus.
 Data terurut: 164, 164, 166, 166, 166, 167, 168, 169, 171, 172.
 Modus data tersebut adalah 166 karena paling sering
muncul, yaitu sebanyak 3 kali.
 PENGETAHUAN : Kelas A mempunyai banyak siswa
yang memiliki tinggi badan 166 cm.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

16. 2.3 MODUS
 Apa kegunaan penggunaan modus? Adakalanya, modus
lebih mencerminkan lokasi kecenderungan
berkumpulnya sebagian besar data dibandingkan ukuran-
ukuran lainnya.
 Sebuah perusahaan menyatakan bahwa rata-rata gaji
karyawannya adalah Rp. 10 juta. Kenyataannya, 90 orang
digaji sekitar 1 juta saja dan hanya 10 orang yang digaji Rp.
100 juta. Dibandingkan rata-rata, informasi yang lebih
berguna dan tidak menyesatkan adalah bahwa sebagian
besar (modus) karyawan sekitar Rp. 1 juta.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

17. 2.4 KUARTIL
 kuartil, data dibagi menjadi empat bagian dan nilai dicari di
tiap seperempat bagian (kuartil) tersebut.
 Data terurut: 164, 164, 166, 166, 166, 167, 168, 169, 171, 172.
 Kuartil pertama = 166
 Kuartil kedua = [(166+167)/2] = 166.5 (sama dengan median)
 Kuartil ketiga = 169
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

18. 3. Deskripsi Keberagaman
 Meskipun deskripsi lokasi sudah memberikan gambaran
tentang lokasi pusat data (rata-rata, median, modus),
keberagaman data belum dapat tergambarkan.
 Meskipun ketiga ukuran lokasi untuk kedua kelompok tepat
sama, apakah kedua kelompok data tersebut dapat dikatakan
serupa? Sama sekali tidak!
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
Kelompok I: 6, 6, 7, 7, 7, 8, 8 (mean=7, median=7, modus=7)
Kelompok II: 0,1, 3, 7, 7, 12, 19 (mean=7, median=7, modus=7)

19. 3. Deskripsi Keberagaman
 Data di kelompok 1 cenderung terkumpul di sekitar 7,
sementara data di kelompok II beragam dan menyebar
lebar hingga menyentuh 0 dan 19.
 Diperlukan pula ukuran keberagaman untuk
melengkapi gambaran kita terhadap data yang ada.
 Tiga ukuran keberagaman yang dibahas adalah range,
varians, dan standar deviasi.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

20. 3. 1. RANGE
 Ukuran sebaran ini menyatakan besarnya rentang jarak
antara data terkecil dengan data terbesar. Rentang yang
besar menandakan bahwa data relatif lebih beragam, dan
sebaliknya, dan sebaliknya.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)

21. Varians dan Standar Deviasi
 Range tidak dapat dijadikan pijakan yang kokoh untuk menilai
keberagaman data. Oleh karena itu, ukuran varians yang menggunakan
prinsip pencarian jarak antara setiap data dengan pusatnya (rata-rata)
seringkali digunakan.
 Secara matematis, hal tersebut dirumuskan menjadi:
 Secara sederhana, rumus tersebut berarti setiap data observasi dikurangi
dengan rata-rata seluruh data. Setiap hasil pengurangan tersebut
dikuadratkan, kemudian semuanya dijumlahkan. Terakhir, hasil
penjumlahan tersebut dibagi dengan (n-1), dengan n yang menyatakan
banyaknya data.
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
n  2(i
x )
s
2

x
i 1
n  1

22. Varians dan Standar Deviasi
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
PENGETAHUAN: Data pada Kelompok II berjarak relatif jauh dengan
pusatnya (dalam hal ini rata-rata) daripada data pada Kelompok I
sehingga variansnya lebih besar. Dengan kata lain, data pada Kelompok II
lebih beragam dibandingkan dengan data pada Kelompok II.

23. Varians dan Standar Deviasi
10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)
Seandainya data di atas memiliki satuan cm, maka varians memiliki satuan cm2.
Hal ini menyebabkan varians menjadi kurang sinkron dengan ukuran-ukuran
lain, seperti rata-rata modus, range, dan lain-lain. Sehingga STANDAR
DEVIASI akan pas untuk digunakan. Standar deviasi yang merupakan akar
kuadrat varians.
Jika ukuran standar deviasi diterapkan pada hasil perhitungan varians di atas,
maka standar deviasi Kelompok I = = 5.5 dan Kelompok II = = 6.7.
PENGETAHUAN: Data pada kelompok II lebih beragam dibandingkan dengan
kelompok I. Jika DATA memiliki satuan cm, maka STANDAR DEVIASInya pun
memiliki satuan cm. Dengan demikian, hasil yang muncul menjadi lebih
mudah dicerna maknanya.

24. 10/30/2019 P.Marpaung : Pert5 (Deskripsi Data Mining)