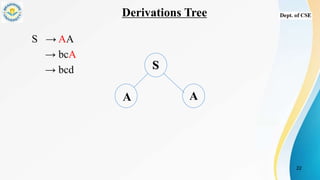
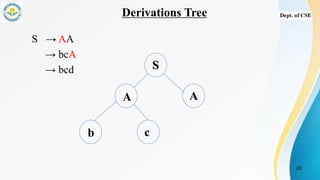
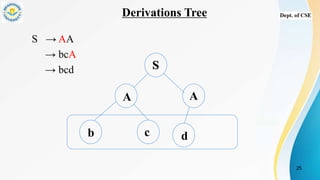
This document provides information about a course on Formal Language and Automata Theory. It discusses: - The course name, code, credits, and number of lectures. - Representation of formal grammars using 4-tuples of sets for alphabets, variables, start symbols, and production rules. - Examples of grammars and derivations of strings to show how strings are generated from a grammar using productions. 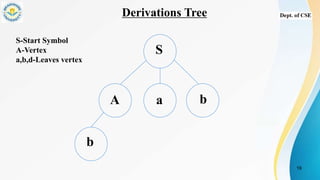- Derivation trees which graphically represent the semantic information of strings derived from a grammar using nodes for start, interior, and leaf symbols. 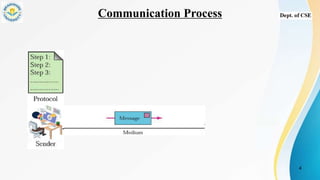- The definition of an automaton as an abstract computing device that follows predetermined operations automatically.

1. Formal Language and Automata
Theory
Shiplu Das
Computer Science and Engineering
Brainware University 1

2. Course Information
• Course Name: Formal Language and Automata Theory
• Course Code: PCC-CS503
• Contact: 3L
• Credits: 3
• No. of Lectures: 36
2

3. Communication Process
3

4. Communication Process
4

5. Communication Process
5

6. Communication Process
6

7. Communication Process
7

8. Langauage
• Alphabets {A,B,C.....Z}
• Words
Grammar
• Sentences {Let us discuss formal language}
• Paragraphs.
8

9. Representation of Grammar
• A grammar G can be formally written as a 4-tuple (N, T, S, P)
where −
N is a set of variables or non-terminal symbols.{1,2,3..E,T,F,V...}
T is a set of terminal symbols.{x,y,z...,+,-,*,/...}
S is a special variable called the Start symbol
P is Production rules for Terminals and Non-terminals. A
production rule has the form α → β
9

10. Example
• Grammar G1 −({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
S, A, and B are Non-terminal symbols.
a and b are Terminal symbols.
S is the Start symbol.
Productions, P : S → AB, A → a, B → b
10

11. Example
• Grammar G2 −({A, B}, {a, b, c}, B, {A → B, A → a, A→c,
B → b, B→A})
A, and B are Non-terminal symbols.
a , b and c are Terminal symbols.
B is the Start symbol.
Productions, P : A → B, A → a, A→c,B → b, B→A
11

12. Example
• Grammar G2 −({A, B}, {a, b, c}, P, {A → B, A → a, A→c,
B → b, B→A})
Wrong Grammar
12

13. Derivations Strings from a Grammar
Example
• Let us consider the grammar −
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → b } )
Some of the strings that can be derived are −
S ⇒ aAb (S → aAb)
⇒ aaAbb (aA → aAb)
⇒ aabbb (A → b) Accepted Strings
13

14. Derivations Strings from a Grammar
Example
G={S → aS , S → B, B → b and B → bB} where S is Start
symbol.
S → B → b (Accepted)
S → B → bB → bb (Accepted)
S → aS → aB → ab (Accepted)
S → aS → aaS → aaB → aab(Accepted)
S → aS → aB → abB → abb (Accepted)
14

15. Derivations Tree
• A derivation tree is an ordered rooted tree that graphically
represents the semantic information a string derived from
grammar.
15

16. Derivations Tree
Representation Technique
• Root vertex
• Vertex
• Leaves vertex
The root node is always a node indicating start symbols.
The leaf node is always terminal nodes.
The interior nodes are always the non-terminal nodes.
16

17. Derivations Tree
17
Start Symbol
Non Terminal
Terminal

18. Derivations Tree
18
S
b
a
A
b

19. Derivations Tree
19
S
b
a
A
b
S-Start Symbol
A-Vertex
a,b,d-Leaves vertex

20. Derivations Tree
Example1:
Let a G1 {N,T,P,S} be
N = {S}, T = {b,c,d}, Starting symbol = S, P = {S → AA
,A→bc,A→d}
One derivation tree from the above string is “bcd”
S → AA
→ bcA (A→bc)
→ bcd (A→d)
→ bcd Accepted
20

21. Derivations Tree
S → AA
→ bcA
→ bcd
21
S

22. Derivations Tree
S → AA
→ bcA
→ bcd
22
S
A A

23. Derivations Tree
S → AA
→ bcA
→ bcd
23
S
A A
b c

24. Derivations Tree
S → AA
→ bcA
→ bcd
24
S
A A
b c d

25. Derivations Tree
S → AA
→ bcA
→ bcd
25
S
A A
b c d

26. Derivations Tree
Example:
Let a G1 {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | c
One derivation from the above string is “acbc”
S → SS
→ aSbS (S→aSb)
→ acbS (S→c)
→ acbc (S→c)
26

27. Automata
• The term "Automata" is derived from the Greek word "αὐτόματα" which
means "self-acting".
• An automaton (Automata in plural) is an abstract computing device
which follows a predetermined sequence of operations automatically.
27

28. Thank You
28