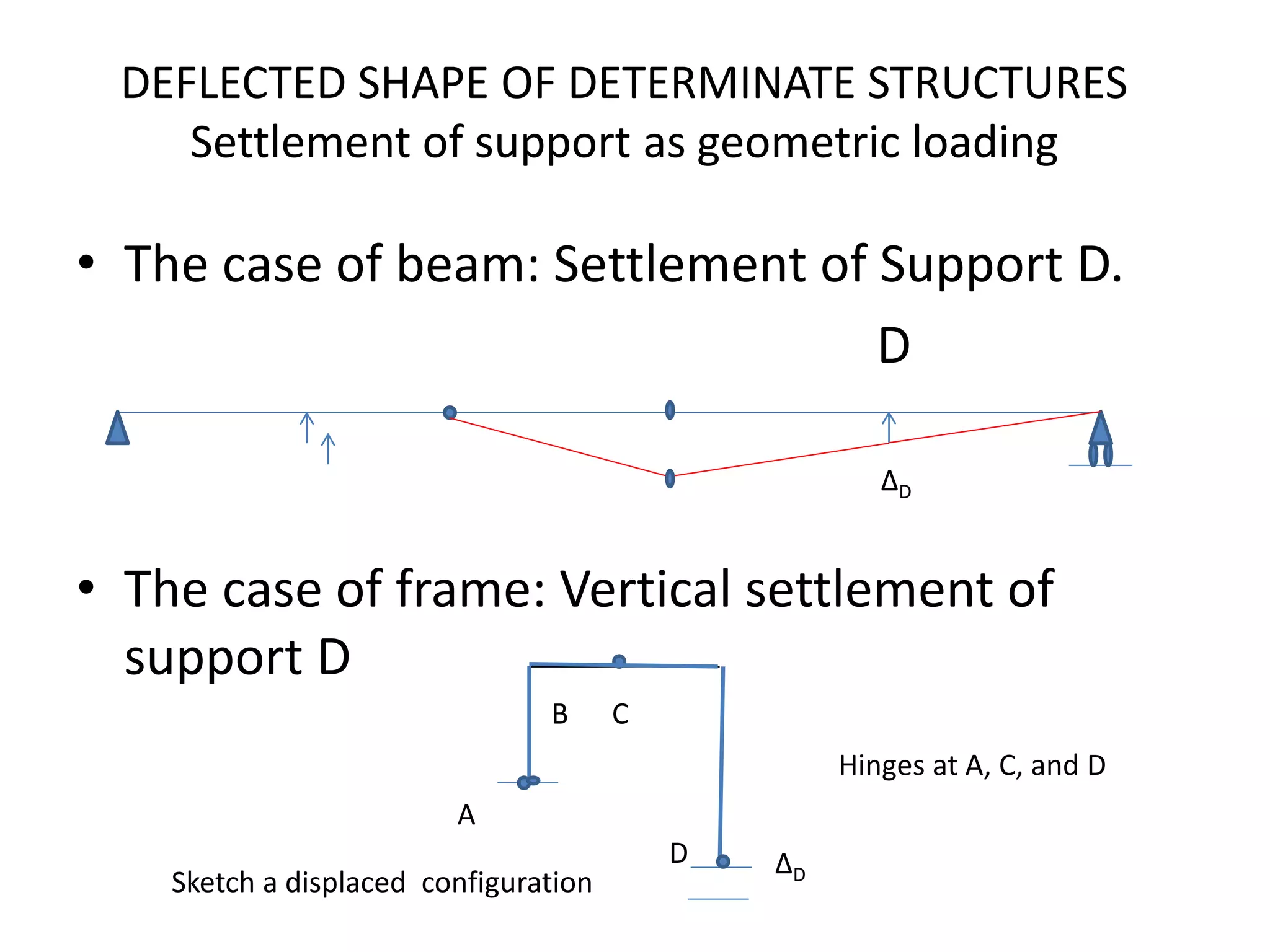
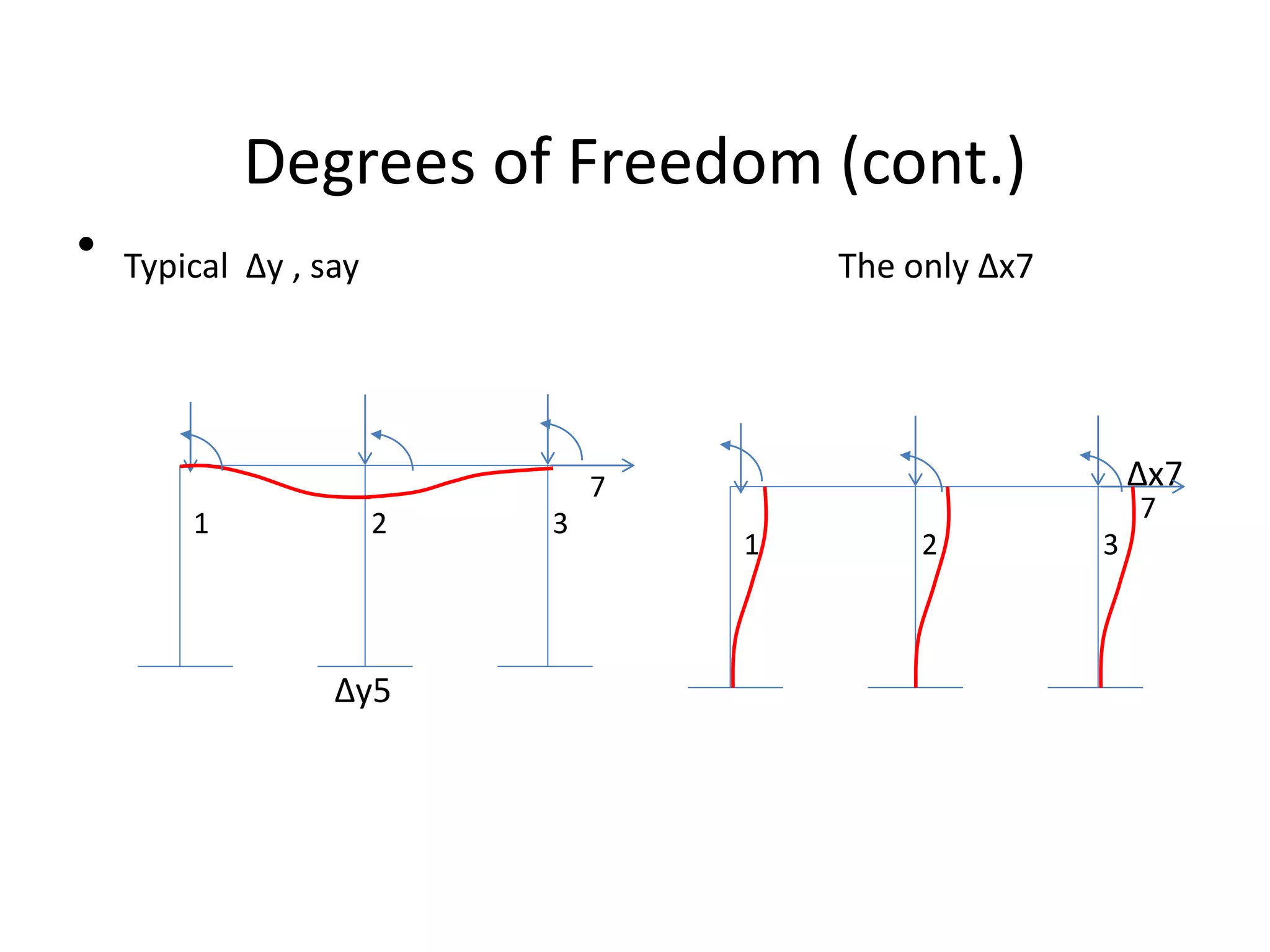
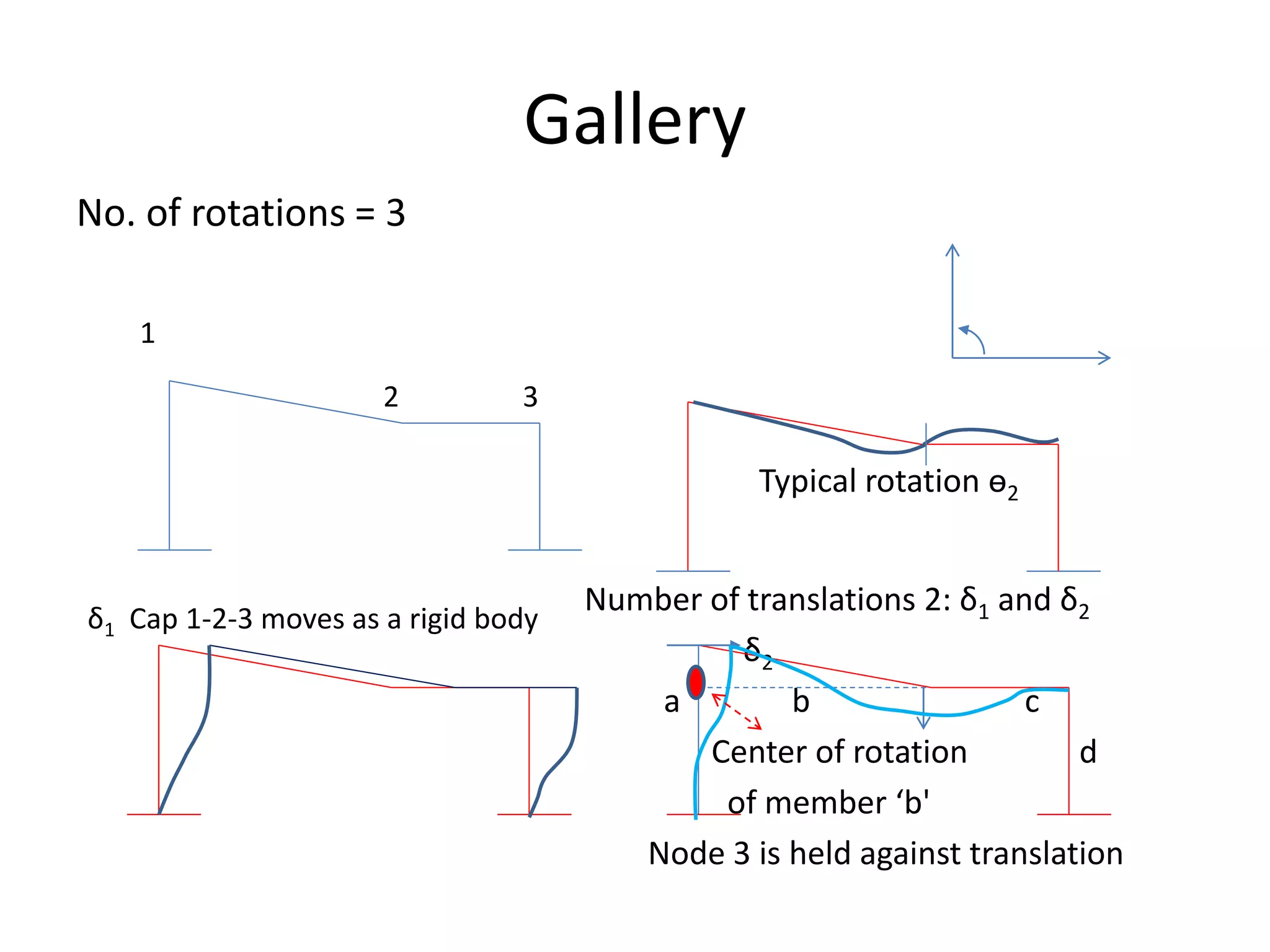
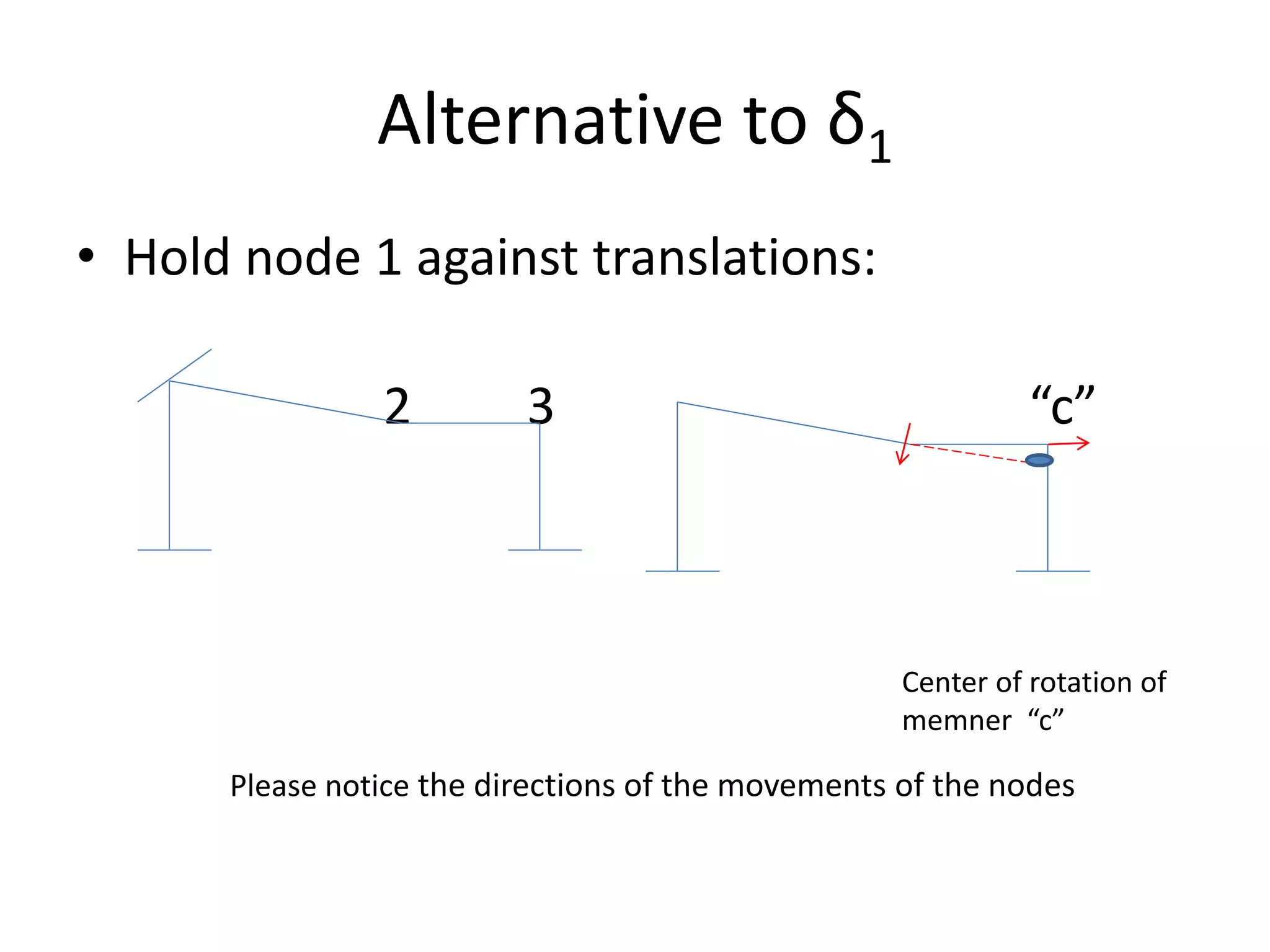
This document discusses analysis methods for structures, including force methods and displacement methods. The force method involves choosing releases to address structural indeterminacy and applying equilibrium equations. The displacement method involves determining degrees of freedom based on assumptions about member inextensibility and applying compatibility equations. Iterative techniques like moment distribution and Kani's method can be used for numerical solutions. Assumptions around member behavior and structural constraints impact the analysis method and results.

1. PART - 2
1. Geometric Loading
2. Force Method and Releases for
achieving the Minimum constraints
3. Displacement Method
4. Assumptions and Degrees of
Freedom

2. GEOMETRIC LOADINGS
• SETTLEMENT
• LACK OF FIT
• TEMPERATURE EFFECTS: UNIFORM RISE
VARYING TEMPERATURE ACROSS DEPTH

3. Force Method
• Indeterminacy from the kinematic
considerations
• Choice of releases
• Generalized Matrix presentation
• Unified Force Method based on Energy
Principles. The releases are generated within
the procedure.

4. A Method based on ‘Structural Anatomy’
• Intuitively, you begin to feel whether the structure is stable!
• If Determinate , the structure has the minimum constraints
from internal and external (support conditions) considerations
• If Indeterminate find the excess constraints, i.e., n
• Analysis using the force method, we choose the n releases.
Which releases? The choice is with us. Use it properly
• Proceed with the analysis for given loads, Gravity, Geometry
based, and Lateral loads (Wind/Earthquake). Read the book
for the details of Analysis
• Assumptions regarding Inextensibility. They do not change n.
This is in contrast to the ‘Inextensibility sensitive’ based
Independent Displacements.

5. Displacement Method
Once, you Identify the nodes based on
1. Geometry, and
2. assumption regarding Inextensibility,
we determine the Number of Unknown Displacements and
proceed with the Analysis by the Displacement Method.

6. Comparison
Force Method
• Preliminaries: Choose
proper releases equal to n.
for Given Loading find
(draw) mo, and mi]i=1,..,n
• Sequential Steps:
1. Equilibrium, Pm = [B0 B] [Pj Q]T
2. Generalized stress-strain relation
ship, and
3. Compatibility.
[Dj U]T [Pj Q]T
Displacement Method
• Choose nodes. Determine
Degrees of Freedom based
on inextensibilities. Find
Nodal Loads for Given
Loading
• Sequential Steps:
1. Compatibility, dm = A dj
2. Generalized stress-strain relation
ship, and
3. Equilibrium.
Pj = {[A]T Km [A]} dj
•
F

7. DEFLECTED SHAPE OF DETERMINATE STRUCTURES
Settlement of support as geometric loading
• The case of beam: Settlement of Support D.
D
• The case of frame: Vertical settlement of
support D
ΔD
ΔD
D
B C
A
Hinges at A, C, and D
Sketch a displaced configuration

8. INEXTENSIBILITY OF MEMBERS IS YET ANOTHER IMPORTANT ASSUMPTION
• FORCE METHOD:
The number of the Unknown
redundants do not with or without
the assumption of inextensibility.
Rib shortening of the Arches is an
illustration of not assuming
Inextensibility
• DISPLACEMENT METHOD:
THE NUMBER OF UNKNOWN
DISPLACEMENTS/ DEGREES OF FREEDOM
ARE GOVERNED BY THE ASSUMPTION.
Generally Girders are assumed inextensible
Illustration:
State degrees of freedom for girders assumed
inextensible. Draw typical rotation, vertical
displacement, and horizontal displacement.

9. Degrees of freedom
Girders only are inextensible
Seven Degrees of Freedom
• Typical rotation
Three rotations, three vertical Δy
and one sway Δ7
• Rotation 1 is sketched.
1 2 3
4 5 6
7
1 2 3
4 5 6
7

10. Degrees of Freedom (cont.)
• Typical Δy , say The only Δx7
Δx7
Δy5
1 2 3
7
1 2 3
7

11. ITERATIVE TECHNIQUES
• Incremental Iteration
Moment Distribution or
Hardy- Cross Method
• Iteration
Kani’s Method

12. No. of rotations = 3
Typical rotation ɵ2
Number of translations 2: δ1 and δ2
δ2
a b c
Center of rotation d
of member ‘b'
Node 3 is held against translation
Gallery
1
2 3
δ1 Cap 1-2-3 moves as a rigid body

13. Alternative to δ1
• Hold node 1 against translations:
2 3 “c”
Please notice the directions of the movements of the nodes
Center of rotation of
memner “c”

14. REVISION PROBLEM
FORCE METHOD AND DISPLACEMENT METHOD
Awareness of implications of Assumptions and
Approximation
• Find degree of
indeterminacy:
• Find Degrees of Freedom:
1. All members inextensible,
2. Girder BD alone is inextensible
(Refer next slide), &
3. Inextensibility is not assumed
Sketch displacements for the cases 1,
2, and 3.
B D

15. Quiz: Find dof of ‘A’ Frame
• All members inextensible, and Girder BD is in
addition flexurally rigid: dof = 2
E E
Net rotation at E is from summation of the above two rotations of joint E.
Associate Deflected shape with the corresponding degree of freedom.
B
D

16. Iterative Techniques for numerical solution of
‘Displacement Method of Analysis’
1. For the ‘Online presentation’, the following are re-emphasized:
The two methods are based on Incremental iteration (Moment Distribution )
and Iteration (Kani’s method)
2. Even though the entire iterative operation is illustrated on the joints and the
ends of the members, Kani’s method is a mere ‘algorithm’ for the joint
rotation and sway combined.
3. Even though the incremental operations pertain to Joint rotations only, the
operations consist of :
(a) clamping the nodes,
(b) Releasing the joints in a proper sequence and then Balancing the moments
joint wise, and
(c ) carrying over the effects joint-wise releasing to the far clamped ends.The
operations and corresponding feel of the structure are commendable.
Hardy Cross the author of the moment distribution made a signal contribution by
giving us a numerical process, which is highly conceptual.