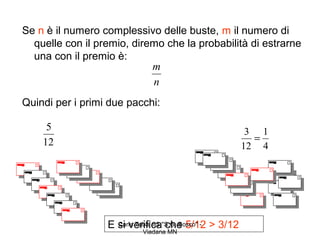
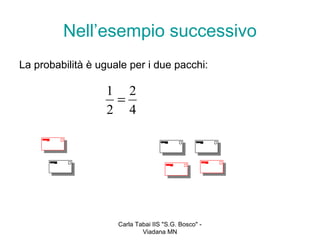
Il documento discute la probabilità attraverso vari esempi, tra cui la ricerca di biglietti d'oro in tavolette di cioccolato e la scelta tra pacchi con buste premi, evidenziando l'importanza del rapporto tra il numero di premi e il totale. Vengono forniti esempi pratici, come il lancio di un dado e la scelta di palline colorate, per illustrare i concetti probabilistici. Infine, si presentano esercizi per applicare le nozioni apprese in vari scenari reali.

1. Parliamo di probabilità
Cinque biglietti d'oro sono nascosti in altrettante tavolette
di cioccolato fabbricate dal signor Willy Wonka. I bambini
fortunati che riusciranno a trovarli potranno varcare i
cancelli della Fabbrica di Cioccolato del signor Wonka ed
entrare così in contatto con il suo magico mondo. Per
Charlie Bucket, un bambino povero, vincitore dell'ultimo
biglietto, sta per iniziare
un'indimenticabile avventura...
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

2. È più probabile trovare il biglietto vincente
comprando una sola tavoletta o dieci tavolette?
Se in tutto il mondo
sono state vendute
milioni di tavolette di
cioccolato, qual era la
probabilità per
Charlie, che ne ha
acquistate due, di
essere vincitore?
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

3. Tutti d’accordo!!!!
Se dobbiamo scegliere una busta fra due diversi pacchi
(ciascuno con 12 buste uguali), ma sappiamo che nel
primo pacco 5 buste contengono un premio, mentre nel
secondo pacco solo 3 lo contengono, nessuno avrebbe
dubbi nel scegliere dal primo pacco.
Pur non essendo sicuri di trovare il premio nella busta,
sappiamo che questo evento è più probabile nel primo
pacco.
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

4. Di nuovo tutti d’accordo …
Se dobbiamo scegliere una busta fra due diversi pacchi con la
seguente situazione:
2 buste di cui 1 con il premio
4 buste di cui 2 con il premio
La probabilità di un esito favorevole è la stessa per i due pacchi e così
sarebbero equivalenti le seguenti due situazioni:
5 buste di cui 2 con il premio
15 buste di cui 6 con il premio
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

5. Che cosa è importante???
Consideriamo ancora due pacchi, ma con questa nuova
situazione:
16 buste di cui 3 con il premio
8 buste di cui 2 con il premio
Nel secondo pacco la situazione è equivalente ad avere
16 buste di cui 4 con il premio; di conseguenza il secondo
pacco è più favorevole.
CIO’ CHE E’ IMPORTANTE E’ IL RAPPORTO FRA IL
NUMERO DELLE BUSTE CON IL PREMIO
E IL NUMERO TOTALE!!!!
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

6. Se n è il numero complessivo delle buste, m il numero di
quelle con il premio, diremo che la probabilità di estrarne
una con il premio è:
m
n
Quindi per i primi due pacchi:
5 3 1
12 =
12 4
E si verifica"S.G. Bosco" - > 3/12
Carla Tabai IIS che 5/12
Viadana MN

7. Nell’esempio successivo
La probabilità è uguale per i due pacchi:
1 2
=
2 4
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

8. Altro esempio
Se lanciamo un dado, ognuna delle sei facce ha la stessa
probabilità di comparire, cioè
1
6
Domanda:
Qual è la probabilità che in un lancio
compaia un numero pari?
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

9. L’evento “numero pari” si realizza quando compare
uno dei tre numeri: 2, 4, 6.
Dunque la probabilità
cercata è
3 1
=
6 2
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

10. DIREMO CHE
per n eventi con uguale probabilità
(come nell’esempio del lancio di un dado
o nell’estrazione delle palline di una tombola)
ognuno degli eventi ha probabilità uguale a
1
n
Se un evento è composto da m eventi elementari, la sua
probabilità è data da
m numero dei casi favorevoli
=
n numero dei casi possibili
Carla Tabai IIS "S.G. Bosco" -
Viadana MN

11. Esercizi
• Disporre in ordine crescente frazioni (con denominatori ad una sola cifra)
Per esempio 2/5,1/3, 3/7, 7/8, 3/4, 2/9, ecc.
• Calcolare la probabilità (con estrazioni di una pallina a caso avendo a
disposizione palline di colori diversi).
Per esempio sacchetto con 28 palline di cui 5 rosse, 15 blu, 2 verdi e 6 gialle .
Risolvere nei due casi (senza reimmissione pallina estratta o con reimmissione)
• Un professore per interrogare estrae a sorte da un sacchetto che contiene 30
palline, numerate da 1 a 30. Nelle classi con meno di 30 alunni procede così: se
esce un numero che è sul registro interroga il ragazzo che corrisponde a quel
numero, se il numero supera quelli del registro fa la somma delle cifre. Calcola la
probabilità che ciascuno ragazzo ha di essere interrogato in una classe di 23
allievi.
• Calcolare la probabilità che esca almeno una volta il 5, lanciando per due volte
un dado
• Bruno percorre un’autostrada e ha carburante sufficiente per 50km. Sa che nei
prossimi 50km ci sono 3 distributori e vorrebbe rifornirsi da quello più economico,
ma non sa le tariffe (e in autostrada non si può tornare indietro …).
Quale strategia consigliereste che renda massima la probabilità di rifornirsi dal
distributore meno costoso?
Carla Tabai IIS "S.G. Bosco" -
Viadana MN