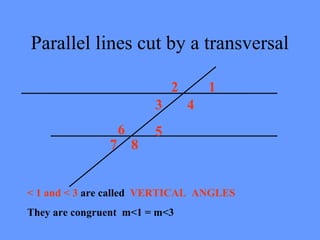
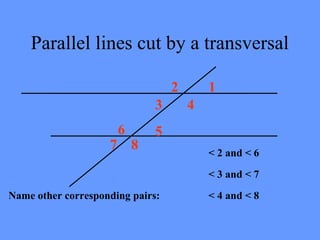
This document defines key terms related to parallel lines cut by a transversal including parallel, transversal, angle, vertical angle, corresponding angle, alternate interior angle, and alternate exterior angle. It provides examples of parallel lines cut by a transversal and identifies pairs of angles that are supplementary, vertical, corresponding, and alternate interior. It gives examples of problems identifying angle relationships and setting up and solving equations based on those relationships. Supplementary angles add to 180 degrees, corresponding angles are equal and in the same position relative to the parallel lines, and alternate interior angles are equal and on the inside of the parallel lines on opposite sides of the transversal.

1. PARALLEL LINES CUT BY A
TRANSVERSAL

2. DEFINITIONS
• PARALLEL
• TRANSVERSAL
• ANGLE
• VERTICAL ANGLE
• CORRESPONDING ANGLE
• ALTERNATE INTERIOR ANGLE
• ALTERNATE EXTERIOR ANGLE

3. DEFINITIONS
• SUPPLEMENTARY ANGLE
• COMPLEMENTARY ANGLE
• CONGRUENT

4. Parallel lines cut by a transversal
12
3 4
56
7 8

5. Parallel lines cut by a transversal
12
3 4
56
7 8
< 1 and < 2 are called SUPLEMENTARY ANGLES
They form a straight angle measuring 180 degrees.

6. Parallel lines cut by a transversal
12
3 4
56
7 8
Name other supplementary pairs:
< 2 and < 3
< 3 and < 4
< 4 and < 1
< 5 and < 6
< 6 and < 7
< 7 and < 8
< 8 and < 5

7. Parallel lines cut by a transversal
12
3 4
56
7 8
< 1 and < 3 are called VERTICAL ANGLES
They are congruent m<1 = m<3

8. Parallel lines cut by a transversal
12
3 4
56
7 8
Name other vertical pairs:
< 2 and < 4
< 6 and < 8
< 5 and < 7

9. Parallel lines cut by a transversal
12
3 4
56
7 8
< 1 and < 5 are called CORRESPONDING ANGLES
They are congruent m<1 = m<5
Corresponding angles occupy the same position on the top and
bottom parallel lines.

10. Parallel lines cut by a transversal
12
3 4
56
7 8
Name other corresponding pairs:
< 2 and < 6
< 3 and < 7
< 4 and < 8

11. Parallel lines cut by a transversal
12
3 4
56
7 8
< 4 and < 6 are called ALTERNATE INTERIOR ANGLES
They are congruent m<4 = m<6
Alternate Interior on on the inside of the two parallel lines and
on opposite sides of the transversal.

12. Parallel lines cut by a transversal
12
3 4
56
7 8
Name other alternate interior pairs:
< 3 and < 5

13. Parallel lines cut by a transversal
12
3 4
56
7 8
Name other alternate exterior pairs:
< 2 and < 8
< 1 and < 7

14. TRY IT OUT
12
3 4
56
7 8
The m < 1 is 60 degrees.
What is the m<2 ?
120 degrees

15. TRY IT OUT
12
3 4
56
7 8
The m < 1 is 60 degrees.
What is the m<5 ?
60 degrees

16. TRY IT OUT
12
3 4
56
7 8
The m < 1 is 60 degrees.
What is the m<3 ?
60 degrees

17. TRY IT OUT
60120
60 120
60120
60 120

18. TRY IT OUT
x + 102x + 20
What do you know about the angles?
Write the equation.
Solve for x.
SUPPLEMENTARY
2x + 20 + x + 10 = 180
3x + 30 = 180
3x = 150
x = 30

19. TRY IT OUT
2x - 60
3x - 120
What do you know about the angles?
Write the equation.
Solve for x.
ALTERNATE INTERIOR
3x - 120 = 2x - 60
x = 60
Subtract 2x from both sides
Add 120 to both sides

20. WEBSITES FOR PRACTICE
Ask Dr. Math: Corresponding /Alternate Angles
Project Interactive: Parallel Lines cut by Transversal