This paper presents a demand-driven approach to inter-procedural data flow analysis that avoids generating redundant analysis results by only computing the necessary data flow facts needed to answer specific queries. The algorithm performs a reverse data flow analysis starting from the query point using a reverse flow function. This approach can answer queries more efficiently than traditional exhaustive data flow analysis.








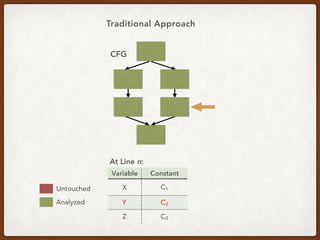
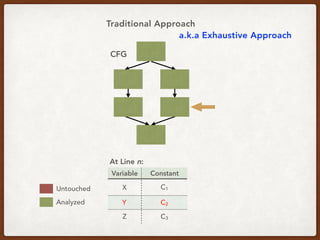
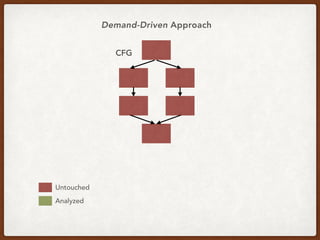
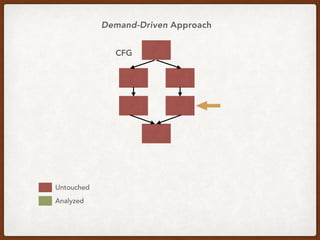
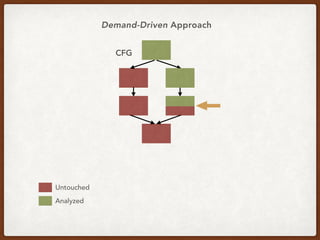
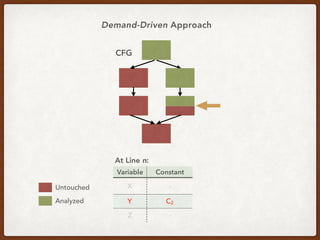
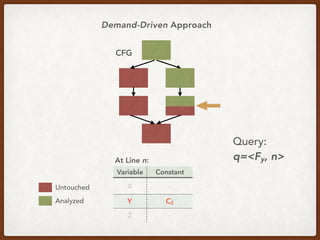

















![An Example Query in CCP*
q := <[a=c], 10>
“Tell me if variable a is equal to constant c at line 10”](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-41-320.jpg)
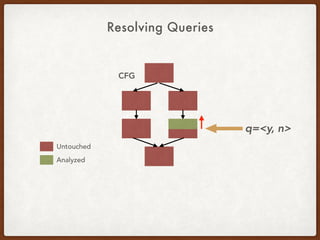
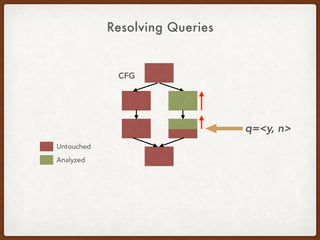
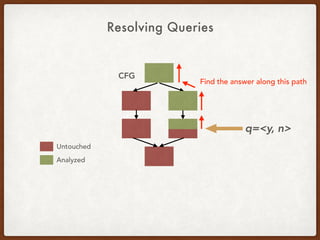
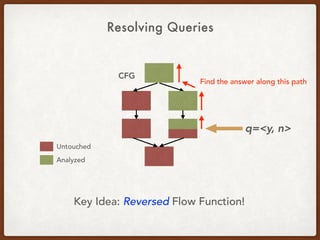





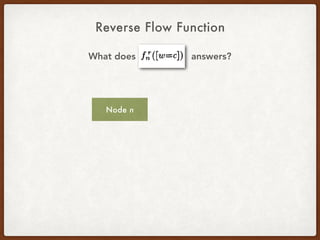

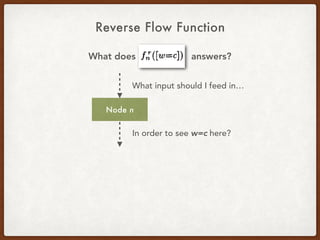










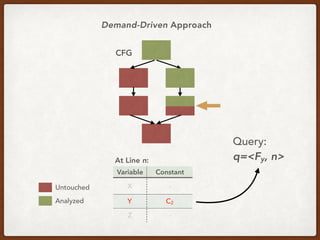
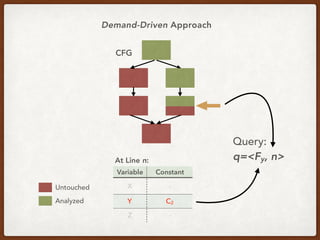
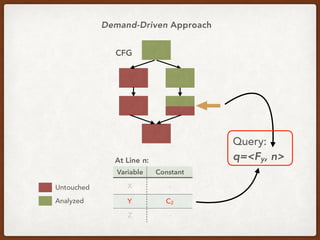
![Generalizing the CCP Query
q := <[a=c], 10>
“Tell me if variable a is equal to constant c at line 10”](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-66-320.jpg)
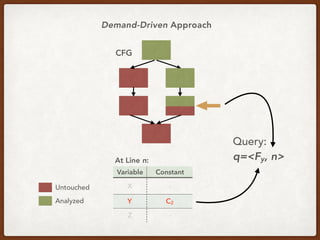
![Generalizing the CCP Query
q := <[a=c], 10>
“Tell me if variable a is equal to constant c at line 10”
What c should we ask?](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-67-320.jpg)
![Generalizing the CCP Query
q := <[a=c], 10>
“Tell me if variable a is equal to constant c at line 10”
What c should we ask?
A more useful query:
“Tell me the constant value (if it is) of variable a at line 10.”
q’ := <[a], 10>](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-68-320.jpg)



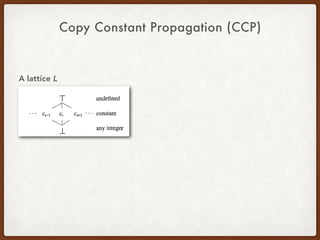
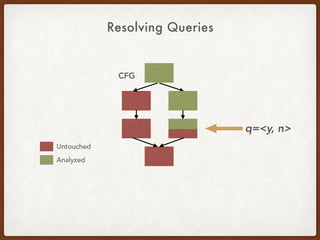
![Generalized CCP Query - A Simple Example
x = 3
y = 4
a = x
r = a + 1 <[a], n>](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-72-320.jpg)
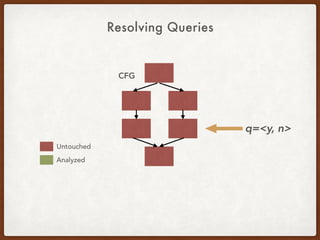
![Generalized CCP Query - A Simple Example
x = 3
y = 4
a = x
r = a + 1 <[a], n>](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-73-320.jpg)
![Generalized CCP Query - A Simple Example
x = 3
y = 4
a = x
r = a + 1 <[a], n>
Final answer for this query](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-74-320.jpg)
![Generalized CCP Query - A Simple Example
x = 3
y = 4
a = x
r = a + 1 <[a], n>
Final answer for this query](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-75-320.jpg)
![Generalized CCP Query - A Simple Example
x = 3
y = 4
a = x
r = a + 1 <[a], n>
Final answer for this query](https://image.slidesharecdn.com/presentation-demand-driven-data-flow-analysis-191128041415/85/Paper-Study-Demand-Driven-Computation-of-Interprocedural-Data-Flow-76-320.jpg)