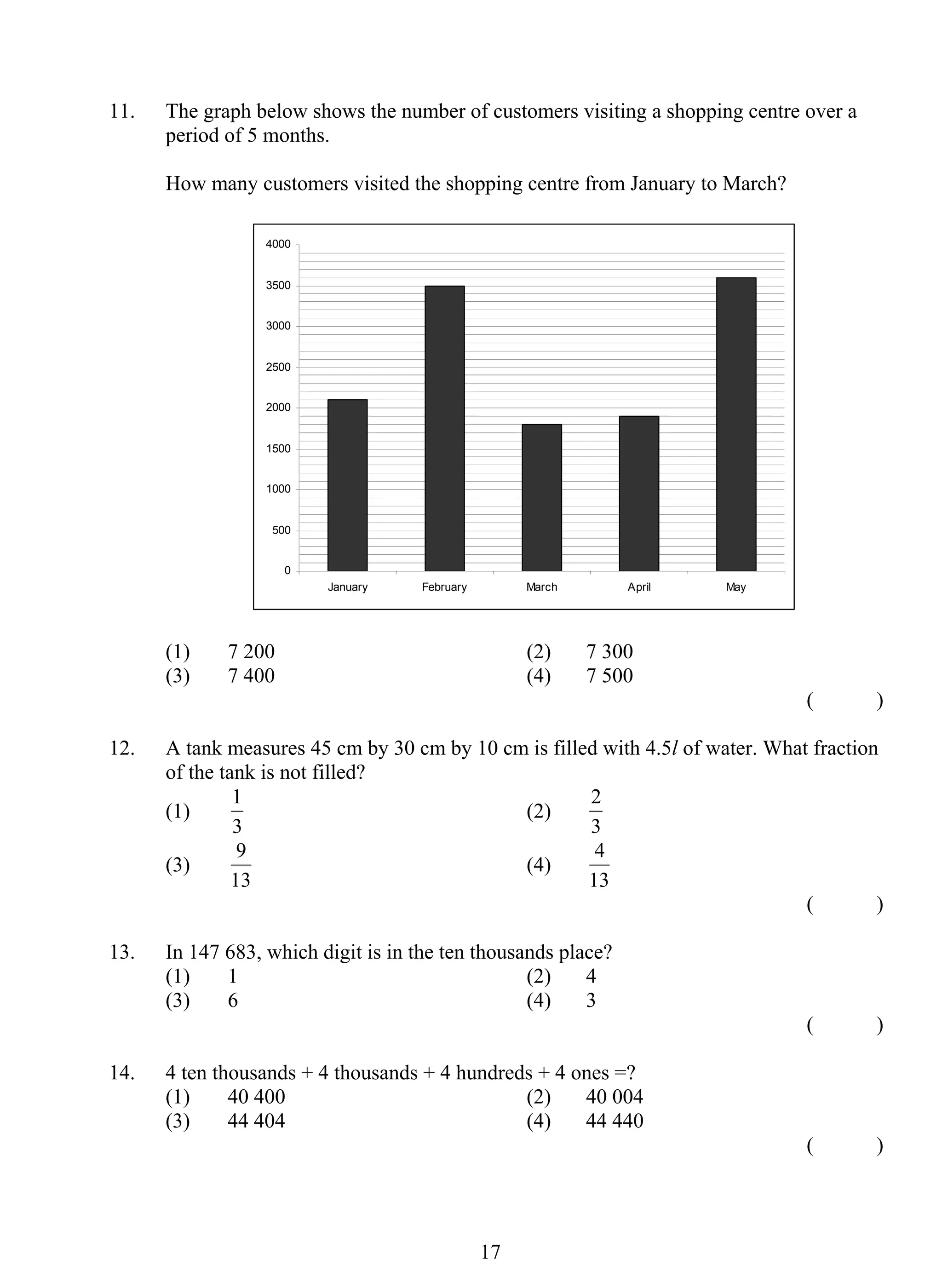
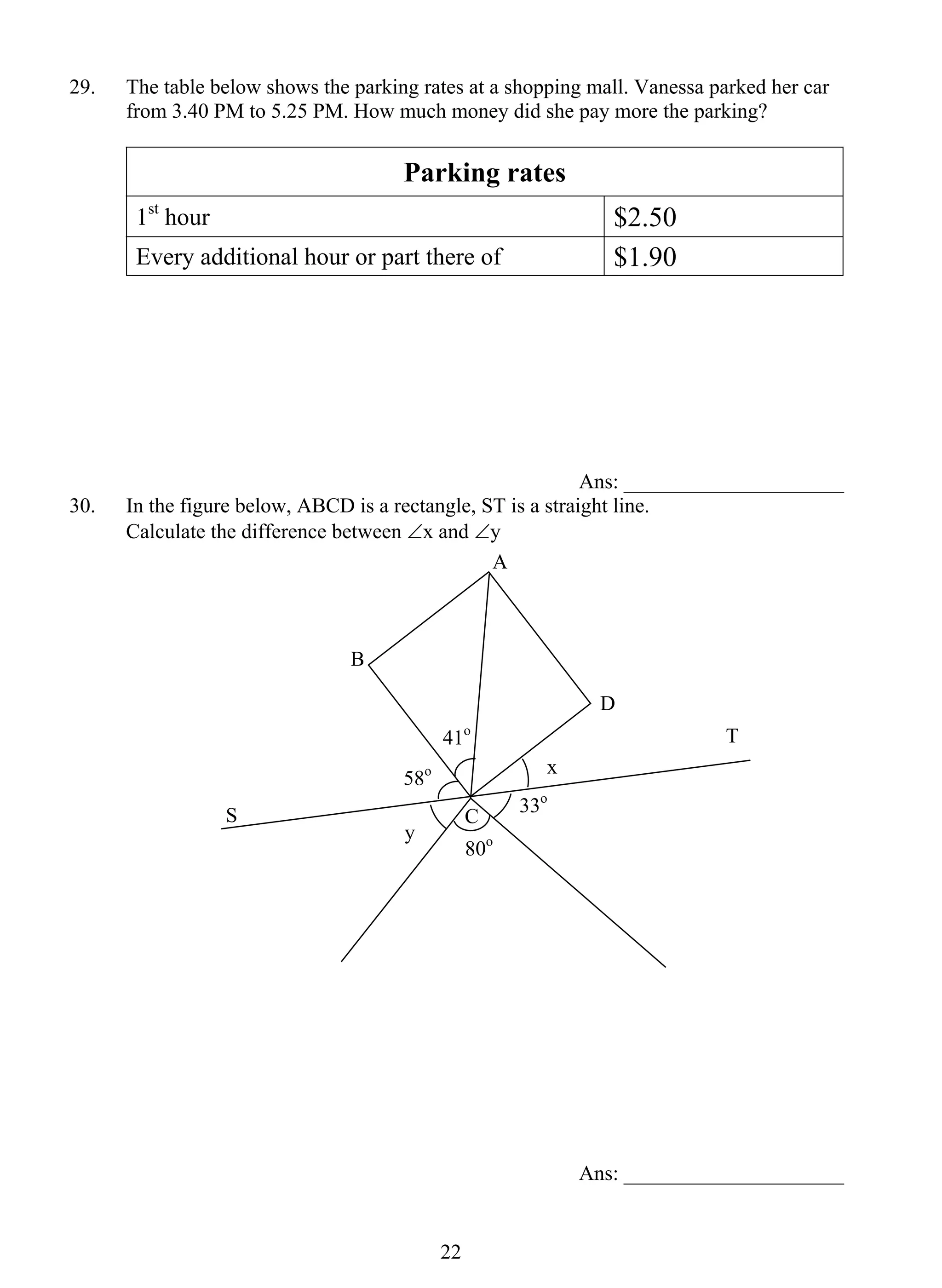
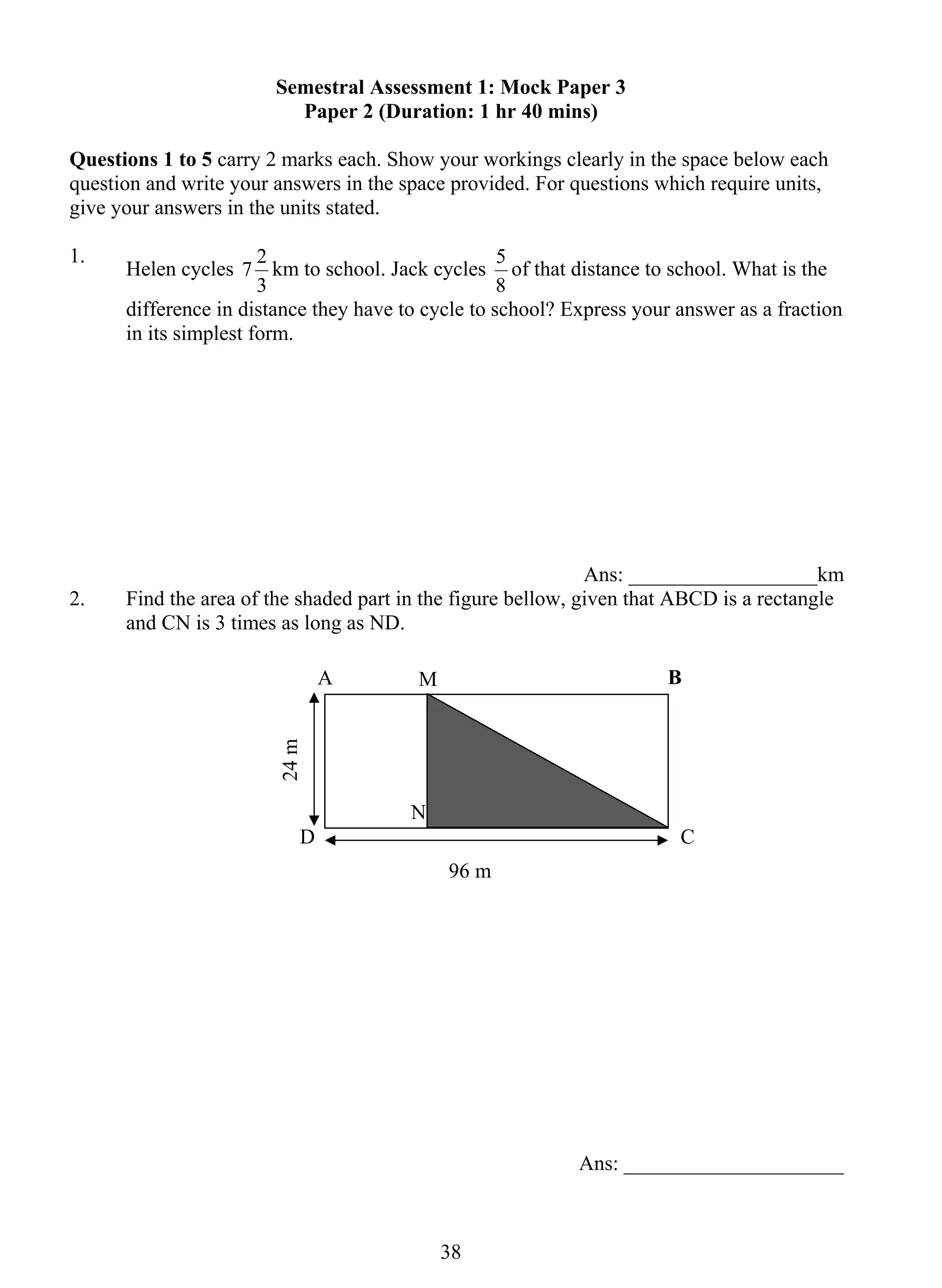
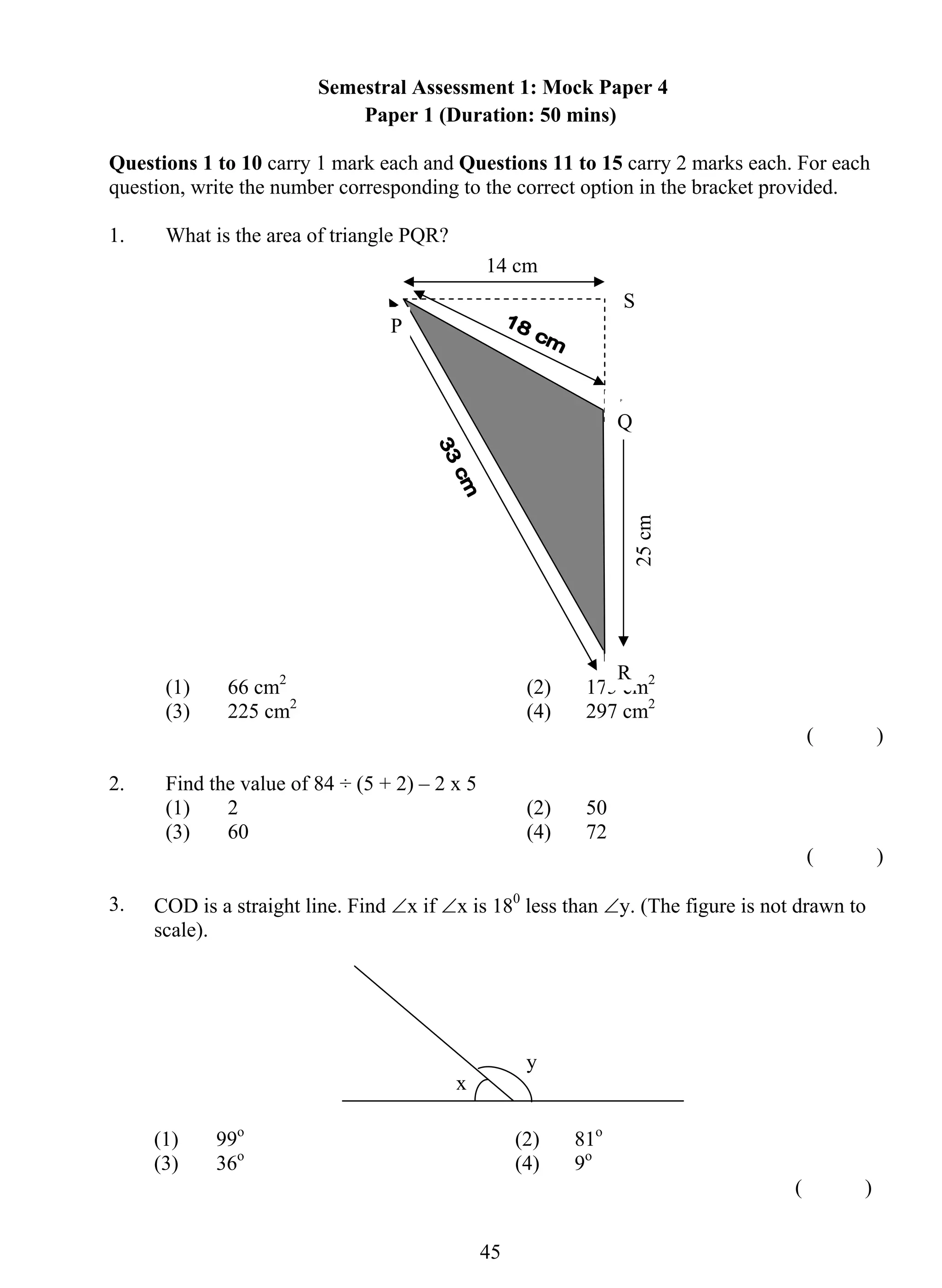
The document provides information about a book titled "Primary 5 Mathematics Ace The Exams with My 24/7 Personal Tutor" which contains 10 examination papers modeled after top Singapore school exams to help students prepare. It also includes a CD with detailed explanations by tutors of all questions. The book and online resources are aimed at helping students understand concepts and identify common misconceptions.













![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. Given that AB is a line of symmetry in the figure below. Shade the squares to
1 0
complete the symmetric figure
Ans: _____________________[4]
7. The average number of Peter’s stickers and Jordan’s stickers is 924. Peter has 232
more stickers than Jordan. Albert has 172 stickers more than Peter. What fraction of
Albert’s stickers are Jordan’s stickers? Write your answer in its simplest form
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-14-2048.jpg)
![8. Three years from now Dan’s father’s age will be thrice Dan’s age. How old is Dan’s
father now if he was 34 years old when Dan was born?
1 1
Ans: _____________________[4]
9. The houses along a road are numbered from 1 to 150. The house number signs are
made of steel digits. How many digits are needed altogether to number the entire
road?
Ans: _____________________[4]
10. Find the perimeter of the figure below.
Ans: _____________________[4]
5 cm
8 cm
13 cm
36 cm
9 cm
7 cm
4 cm
A
B
5 cm](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-15-2048.jpg)
![11. A shop sells carpets at $15 per square meter. Uncle Tay wants to buy a carpet for his
living room, which is 10m by 7m. How much does he have to pay?
1 2
Ans: _____________________[4]
12. When 60 packs of cookies are placed in a box, the total mass is 6 790g. When the
same box contains 25 packs of cookies, the mass is 4 655g. Find the mass of the box
in kg.
Ans: _____________________[4]
13. Each tourist has to pay $1 215 for a 5-day tour to Vietnam. If there were 116 tourists
who chose that tour last month, how much did the travel agency receive?
Ans: _____________________[3]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-16-2048.jpg)
![14. Create a tessellation in the space provided by drawing 4 more unit shapes.
1 3
Ans: _____________________[4]
15. Alex, Ben and Carl collected a total of 2 151 stamps. Alex collected 224 stamps
fewer Carl. Ben’s collection was 3 times as many as Carl’s. How many stickers did
Carl have?
Ans: _____________________[4]
16. How many lines of symmetry are there in the figure below, given that all line
segments are equal
Ans: _____________________[3]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-17-2048.jpg)
![17. A water tank 90 cm long, 40 cm wide and 15 cm high needed to be filled by two taps
A and B. Tap A, which had a flow rate of 12l per minute, was turned on first. After
11 minutes, tap B, which can flow only
2
1 4
1 as fast as tap A, was turned on and both
3
tap continued to fill the tank. Since both taps were turned on, how long did it take to
fill the tank completely? Express your answer in minutes and seconds.
Ans: _____________________[4]
18. A number of trees were planted around the perimeter of a rectangular parcel of land
that was 49m long and 35m wide. There was a tree in each corner. On each side of
the land trees were planted 7m apart. How many trees were there in total?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-18-2048.jpg)








![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. Study the figures below. The figure on the left shows a rectangular strip of paper.
The figure on the right shows that strip when folded along the dotted line. It consists
of 2 squares and 1 trapezium.
a) Find the length of the paper strip.
b) Find the area of the paper strip
3 cm
7 cm
3 of his money on 18 cakes and 21 toy robots.
2 5
Ans: _____________________[4]
7. Jeffery spent
5
The cost of a toy robot is 2 times that of a cake.
How many more toy robots could he buy with the remaining money?
Ans: _____________________[3]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-29-2048.jpg)
![8. Some girls bought a packet of strawberries to share among themselves. If each girl
took 7 strawberries, there would be 4 extra strawberries. If each girl took 8
strawberries, there would be 4 strawberries short.
a) How many strawberries did they buy?
b) How many girls were there?
7 of what Jason had.
2 6
Ans: _____________________[4]
9. Freddie, Jason and Malik each had some toy cars. Jason and Malik had
11 of what
14
Freddie had, and Malik had
15
a) If Freddie had 56 toy cars, how many toy cars did Jason have?
b) How many toy cars did they have altogether?
Ans: _____________________[4]
10. Mary bought 7 similar notepads and 9 similar pens. Each notepad is $1.1 more
expensive than a pen. If the total money Mary spent was $33.3, how much did she
pay for the pens?
Ans: _____________________[3]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-30-2048.jpg)
![11. Ross paid $85 for 10 notebooks and 4 files. Each notebook cost as much as 3 files.
2 7
What is the price of a notebook?
Ans: _____________________[4]
12. Study the figure below. Note that it is not drawn to scale. Answer the following
questions:
a) What is the area of the unshaded part?
b) What fraction of the whole figure is shaded?
Ans: _____________________[4]
10 cm 18 cm
30 cm](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-31-2048.jpg)
![2 of the fruits in a basket are pears. There are 30 more apples than pears. The rest of
the fruits are 90 oranges. How many more apple than oranges were there?
1 that of the body. How long is the whale skeleton?
2 8
13.
7
Ans: _____________________[4]
14. At a museum, the body of the whale skeleton on display is as long as the total length
of its head and tail. The head of the whale skeleton is 8m long. The length of the tail
is equal to that of the head plus
3
Ans: _____________________[4]
15. A train departed from Clementi station.
5 of the passengers were adults.
11
3 of the
4
children were boys. The number of adult men is
1 that of women. There were 114
4
less girls than boys. At the next station, Dover, 9 women and 5 boys boarded the
train.
a) How many passengers were there altogether when the train left Clementi
Station?
b) How many male passengers were there on the train when it departed from
Dover station?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-32-2048.jpg)
![16. Mrs. Liu bought 5 packets of sugar, A, B, C, D, and E. The mass of sugar in each
packet is 500g, 600g, 800g, 900g and 1kg, respectively. Mrs. Liu kept one packet for
herself and sold the other packets to Mrs. Chan and Mrs. Lim. Mrs. Lim bought
twice the amount of sugar that Mrs. Chan bought. Which packet did Mrs. Liu keep
for herself if she kept more than 500g?
16 her son’s age. Now her age is three times
2 9
Ans: _____________________[4]
17. Alex, Benny, Carol and Dean stand in a straight row. Alex is not standing next to
Dean and Benny does not stand at the first position, how many possible ways are
there to arrange the four pupils?
Ans: _____________________[4]
18. Seven years ago Mrs. Goh’s age was
3
her son’s age. What is Mrs. Goh’s age now?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-33-2048.jpg)









![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. Nancy had some stickers.
1 of them were used to make a scrapbook. She then
2 of the remaining equally to her three friends. After making the scrapbook
4 0
3
divided
3
and sharing stickers to her friends she had 42 stickers less than what she had at the
beginning. How many stickers did each of her friends receive?
Ans: _____________________[4]
7. Suriyana and Fahan each had saved some 20-cent and 50-cent coins. Suriyana had a
total of 192 coins. The number of 20-cent coins that Suriyana had was
3 the number
5
of 50-cent coins that she had. The ratio of the number of 20-cent coins to the number
of 50-cent coins that Fahan had was 1:2. Fahan’s total number of coins is only
1
4
that of Suriyana.
a) What is the ratio of the number of 20-cent coins Suriyana had to the number
of 50-cent coins that Fahan had?
b) What is the ratio of the amount of money that Suriyana had to the amount of
money that Fahan had?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-44-2048.jpg)
![8. Find a number that gives a quotient of 189 and a remainder of 17 when divided by
5 of his working hours working with his computer. He worked for
1 of the day. How many minutes did he work with his computer?
4 1
55.
Ans: _____________________[3]
9. Mr. Ong spent
12
3
Ans: _____________________[3]
10. Tom and Jerry have some money. If Tom gives Jerry $5, he will have half what Jerry
has. If Jerry gives Tom $5, they will have the same amount.
a) How much money does Tom have?
b) How much money does Jerry have?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-45-2048.jpg)
![11. A box of 16 Pelican pens (box A) is sold at $14.70. A box of 24 Pelican pens (box B)
is sold at $22.50. Is box A or box B the cheaper buy?
4 2
Ans: _____________________[4]
12. All the people at a party shake hands with one another. How many handshakes are
there if there are
a) 3 people?
b) 5 people?
c) 10 people?
Ans: _____________________[4]
13. The ratio among 3 sides of a triangle is 4 : 2 : 5. The longest side is 300 cm. What is
the perimeter of the triangle?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-46-2048.jpg)
![4 3
14. Study the following pattern:
1
1
1
5
...
1
1
1
4
1
1
1
4 5
4
3
3 4
3
2
2 3
= −
×
= −
×
= −
×
Use the above pattern to calculate
... 1
19 20
1
4 5
1
3 4
1
2 3
×
+ +
×
+
×
+
×
Give your answer in the simplest form.
Ans: _____________________[4]
15. Mr. Green needed to go from A to B. He had travelled
3 of the distance and still
8
needed to travel another 480km. What is the distance from A to B?
Ans: _____________________[4]
16. A rectangle water tank can contain a maximum of 105m3 of water. Its base is 5m
wide and 7m long. What is the depth of the tank?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-47-2048.jpg)
![17. What is the area of the right-angled trapezium ABCD as shown below?
14 cm
4 4
Ans: _____________________[4]
18. 36 chickens and dogs have a total of 100 legs. How many chickens are there?
Ans: _____________________[4]
A B
D C
26 cm
11 cm](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-48-2048.jpg)







![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. In the figure below, what is the area of the square if the averaged perimeter of the
1 the volume of petrol in barrel B. 24l of petrol
55
square and the triangle is 59 cm?
Ans: _____________________[4]
7. The volume of petrol in barrel A is
4
is moved from barrel B to barrel A. The volume of petrol in barrel A is now
1 the
2
volume of petrol in barrel B. How much petrol is there in barrel B in the end?
Ans: _____________________[4]
28 cm
12 cm](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-59-2048.jpg)
![8. Examine the pattern of the following figure. Find the missing number.
?
56
12
Ans: _____________________[4]
5
9. A shop is selling toy robots at $20 and dolls at $50. There are 23 more dolls than toy
robots. After selling some dolls for $900, the shop has 1.5 times as many dolls as toy
robots. How many dolls did the shop have at first?
Ans: _____________________[3]
89
115
1020
117
258
4500
205
397
4816](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-60-2048.jpg)
![10. Joey, Zhong Ren and Suriya had a total of $1 326. After Joey spent
1 of his money, and Suriya spent
4 the total of cards that George and Harry had. George had twice the number of
cards Fred had.
a) If George had 104 cards, how many did Harry have?
b) What was the number of cards three of them had altogether?
1 of his brother’s money. The product of their money is $400. How much
57
2 of his money,
5
Zhong Ren spent
7
1 of her money, all of them had
3
the same amount of money. How much did they spend altogether?
Ans: _____________________[4]
11. Fred, George and Harry shared some pokemon cards. The number of cards Fred had
is
11
Ans: _____________________[4]
12. Jane had
4
money did Jane have?
Ans: _____________________[3]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-61-2048.jpg)
![13. A pair of shoes is 9 times as expensive as a pair of socks. If 3 pairs of shoes and 5
pairs of socks cost $192, how much is a pair of shoes?
1 times as heavy as a bag of powder. The average mass of the two
58
Ans: _____________________[4]
14. What is the area of the shaded part, if each small square is 4 cm x 4 cm?
Ans: _____________________[4]
15. A bag of rice is 2
2
bags is 33.25 kg. What is the mass of the bag of powder?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-62-2048.jpg)
![16. The ratio of the number of pencils to the number of pens in a stationary shop was 3:
7. The stall owner then sold 36 pens and the number of pens became equal to the
number of pencils. How many pens were there in the shop at first?
59
Ans: _____________________[4]
17. The figure below is not drawn to scale. Find the area of the shaded part.
Ans: _____________________[4]
18. Alice had 9 notepads and Ronald had 6 notepads. Alice then bought some more
notepads. After that the ratio of the number of notepads that she had to the number of
notepads Ronald had is 7: 3. How many more notepads did Alice buy?
Ans: _____________________[4]
19 cm
15 cm
15 cm
7 cm](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-63-2048.jpg)







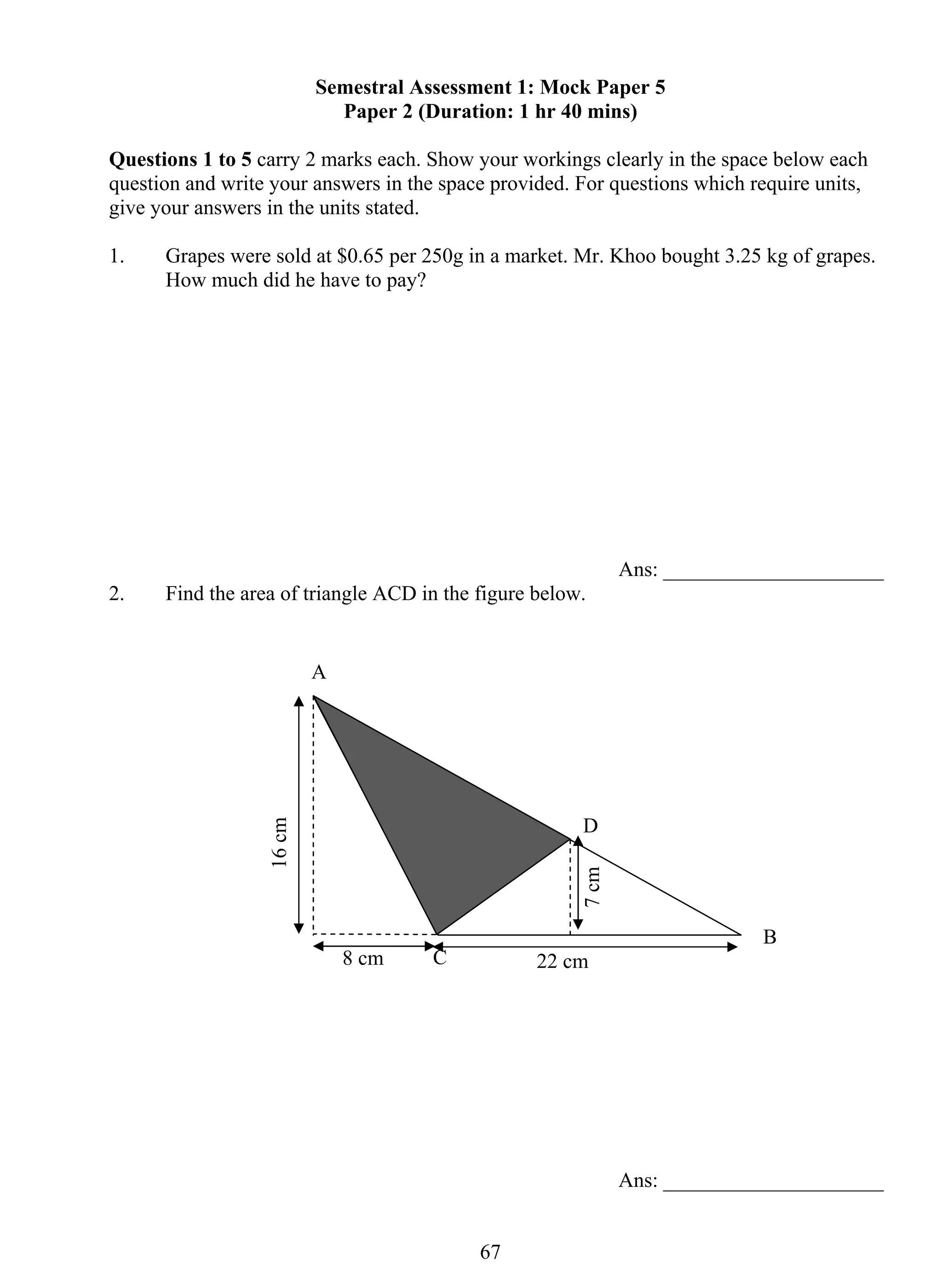

![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. When Tom received his salary, he gave his mother
69
1 his salary. He then used
4
1 of
7
the remaining amount plus $54 to pay his bills. After that, he spent half of the
remainder plus $27 to buy a computer. Finally, he saved the remaining $846. How
much was his salary?
Ans: _______________[4]
7. In the tables and chairs section of a warehouse, the ratio of the number of chairs to
that of tables is 5: 3. There are 64 wooden pieces of furniture and the rest are made
of plastic. The number of plastic pieces is twice the number of wooden pieces. If
there are 32 wooden chairs, what is the ratio of the number of plastic chairs to that of
wooden tables?
Ans: _______________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-73-2048.jpg)
![1 m taller than she is. What is the average height
1 of a magazine on Friday and
70
8. Betsy is 1
1 m tall. Her brother is
2
6
of the two children? Round off your answer to 2 decimal places.
Ans: _______________[4]
9. Nicole read
5
1 of the remaining on Saturday. On
4
Sunday she read twice as many pages as on Friday. What fraction of the magazine
was not read?
Ans: _______________[4]
10. The ratio of the cost of an LCD monitor to that of a computer is
4 . The computer
9
costs $900. What is the average cost of the two devices?
Ans: _______________[3]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-74-2048.jpg)
![11. Ken bought 3 pairs of jeans and 2 shirts for $90. A pair of jeans was $5 more
expensive than a shirt. How much did a pair of jeans cost?
71
Ans: _______________[4]
12. The ratio of the number of Indian pupils to the number of Chinese pupils is 2: 7. The
ratio of the number of Malay pupils to the ratio of Chinese pupils is 3: 4. What is the
ratio of the number of Indian pupils to the number of Malay pupils to the number of
Chinese pupils?
Ans: _______________[4]
13. A bank paid a fixed 0.68% saving interest per year. Bill opened an account and
deposited $172 000. How much interest would he earn after a year?
Ans: __$____________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-75-2048.jpg)
![14. The total amount of money that Soo Hui and Margaret had is $630. If Margaret gave
Soo Hui $52.70, Soo Hui would have eight times the amount that Margaret had.
Initially, what was the difference in the amounts that they had at first?
72
Ans: _______________[4]
15. The total volume of water in tanks A, B and C is 400l. If half of the water in tank A
is taken away and the water in tank B is doubled, and 30l is added to tank C, the ratio
of the volume of water in tank A to B to C will be 3: 2: 1. Find the amount of water
in tank B initially.
Ans: _______________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-76-2048.jpg)
![16. A set of furniture costs $3290. Mr. Tay bought the set with 20% discount. However,
he had to pay 7% GST on the discounted price. How much did he have to pay for the
set of furniture?
73
Ans: _______________[4]
17. Use the following digits, each digit only once, to make the smallest even number that
is greater than 250 000.
0, 3, 7, 2, 9, 6
Ans: _______________[3]
18. In a laboratory, the mass of some bacteria doubles every 12 minutes. If the mass is
128 mg at 5 p.m, what time was it when the mass was 0.5 mg?
Ans: _______________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-77-2048.jpg)








![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. The table below shows the number of days pupils exercised in a week. What is the
fraction of the number of pupils that exercise 2 days or more to the total number of
pupils? Express your answer correct to 2 decimal places.
No. of exercised days 0 1 2 3 4
No. of pupils 5 9 7 16 5
82
Ans: _____________________[3]
7. In a festival that has 2500 participants, there are 1100 females. How many percent
more males than females are there? Round off your answer to 2 decimal places.
Ans: ____________________%[3]
8. The number of exercise questions that 3 pupils have completed is in the ratio of 2: 4:
5. If the pupil who had done the least completed 6 questions, what is the total number
of questions that they have completed?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-86-2048.jpg)
![9. There are approximately 3300 adults and 1700 children in a stadium. If both above
figures are corrected to the nearest hundred, what is the largest possible difference
between these 2 figures?
83
Ans: _____________________[4]
10. The area of the shaded part in the figure below is 54 cm2. SH =
1 PK.
4
What is the area of triangle PQR?
Ans: _____________________[4]
P
S
Q R
H K](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-87-2048.jpg)
![11. The area of rectangle A is 3 times the area of square B. The unshaded area of
rectangle A is 5 times the unshaded area of square B. If the shaded area is 27 cm2,
what is the area of the square? The figure is not to scale.
84
Ans: _____________________[4]
12. Miss Chua brought some lollipops to share equally among 36 pupils at the end of a
camp. However, 9 pupils had to leave the camp early. Therefore, each of the
remaining pupils received 3 more lollipops. How many lollipops did Miss Chua
bring?
Ans: _____________________[4]
A
B](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-88-2048.jpg)
![13. In the figure below, ABC is a right angled triangle at C. Its height is 9 cm and its
base is 12 cm. 4 such identical triangles are used to form the square MNPQ. Find the
side of the square MNPQ.
1 the area of triangle B. The ratio of area of triangle A to that of
85
Ans: _____________________[4]
14. In the figure below, a rectangle is divided into 4 smaller triangles A, B, C and D. The
area of triangle A is
3
triangle D is 3: 5. The width of the rectangle is 6 cm. The area of triangle D is 30
cm2. Find the perimeter of the rectangle.
Ans: _____________________[4]
A
B
C
D
Q
A
C B
M N
P](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-89-2048.jpg)
![15. In a second-hand bookshop, story books are sold at $12 each and comic books are
sold at $8 each. At first, there were 50% more story books than comic books. After
some time,
2 of the story books and all the comic books were sold. The shop
1 the money that Aaron had. After that Aaron spent $45 and Lucy’s
86
3
received $6400. When all the books were sold, how much would the shop receive?
Ans: _____________________[4]
16. Lucy had
3
mother gave her $6. Aaron still had $3 more than Lucy. How much money did Lucy
have at first?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-90-2048.jpg)
![2 the number of marbles that Thomas has. Ben has
87
17.
3 of Joey’s marbles is equal to
5
7
twice the difference between Thomas and Joey’s marbles. Joey has 48 marbles less
than Ben. How many marbles do they have altogether?
Ans: _____________________[4]
18. Tank A measures 4 m by 6 m at the base and is 1 m high. Tank B has the base
dimensions of 5 m x 3 m and is twice as high as tank A. Both of them contain the
same amount of water. The height of water level in tank A is half of its height. Find
the height of water level in tank B.
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-91-2048.jpg)








![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. What is the total mass of a bag that weighs
4 of the previous height for every bounce. Find the total
96
3 of 4500g and a box that weighs 48%
8
of 18 kg? Express your answer in kg correct to 2 decimal places.
Ans: ___________________kg[3]
7. There are 15 trees planted in a line. The distance between any two adjacent trees is
the same. The seventh tree is 7920 cm away from the third tree. How far from the
first tree is the last tree? Express your answer in meters.
Ans: _____________________[4]
8. When dropping a tennis ball from a height of 15m to the ground, Johannes realized
that the ball went up to
5
distance that the ball had travelled when it hit the ground the second time.
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-100-2048.jpg)
![9. Mr. Lee has 4 children. His age is 3 times that of his youngest child. Each child was
born 3 years before the next one. The total age of the 4 children and the father is 193
years. Find the age of Mr. Lee’s first child.
97
Ans: _____________________[4]
10. Each small truck has 10 wheels. Each large truck has 14 wheels. A truck
manufacturer ordered 408 wheels for their 32 trucks. How many large trucks are
there?
Ans: _____________________[4]
11. Francis gave half of his salary plus $100 to his mother. He spent 25% of the
remaining plus $49 on furniture. He bought some books for $61. He gave
3 of his
5
remaining sum plus $53 to his sister. He saved the final $443. How much is Francis’s
salary?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-101-2048.jpg)
![12. An elephant is 5.5 times as heavy as a zebra. The total mass of 2 elephants and 3
zebras is 1260 kg. What is the mass of 1 elephant and 4 zebras?
98
Ans: _____________________[4]
13. From January to August, Phoebe earned an average of $2340 per month. From
September to December, she earned some more money and the average earning over
the entire year is $3290. What was the average amount of money that Phoebe earned
a month in the period from September to December?
Ans: _____________________[4]
14. In a charity event, 3 scouts Benny, Ray and Kathy raised $1459 altogether. Ray
raised $296 less than Benny while Katy raised an amount
1 as much as Benny. How
4
much money did Kathy raise?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-102-2048.jpg)
![15. The ratio of the number of roses to the number of lilies to the number of tulips is
3:5:9. If there are 954 more tulips than roses, how many more lilies than roses are
there?
99
Ans: _____________________[3]
16. There are 20 more pages in a mathematics book than in a physics book. There are 70
more pages in a chemistry book than in a mathematics book. The total number of
pages in 20 books of each type is 10 000. How many pages are there in a physics
book?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-103-2048.jpg)
![17. In the figure below, the rectangle on the left is made by bending a wire. Another wire
with the same length is bent to make the two identical isosceles triangles on the right.
What is the area of one isosceles triangle?
1 on stationeries. He also bought two pairs of shoes
10 0
Ans: _____________________[4]
18. The ratio of the amount of money Josh had to that Derek had was 3: 5. Derek spent
25% of his money on toys and
5
for $150. He saved the remaining $246. How much money did Josh have?
Ans: _____________________[4]
33 cm
75 cm
36 cm](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-104-2048.jpg)









![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. The figure below is not drawn to scale. ∠MNQ is 29o. MNPQ is a rhombus.
Q O
1 of the carton of milk on the first day. Over the next two days he
11 0
a) Find ∠ NMQ.
b) If MN = NO, find ∠ NOP.
Ans: _____________________[4]
7. Guo Qi drank
5
drank 75% of the remaining milk. There was still 750ml of milk left.
What is the volume of the carton of milk? Express your answer in liters.
Ans: _____________________[4]
M
N
P](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-114-2048.jpg)
![8. An apple drink is made by mixing apple syrup and plain water in the ratio 2: 5. How
many milliliters of apple syrup is needed to make 1.4 l of apple drink?
11 1
Ans: _____________________[3]
9. Study the pattern below. The shapes are made by using toothpicks.
a) How many toothpicks are needed to make 5 shapes?
b) How many shapes can be made using 258 toothpicks?
Ans: _____________________[4]
10. The number of stickers that Pamela had is 40% of the number of stickers that Zoe
had. If the two children had 952 stickers altogether, how many stickers did Zoe
have?
Ans: _____________________[3]
1 shape 2 shapes 3 shapes](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-115-2048.jpg)
![5 that of Chek Khoon and Chek Khoon is 4kg more than Darren. If
11 2
11. Bala’s weight is
6
the average mass of the three boys is 44 kg, what is the mass of Chek Khoon?
Ans: _____________________[4]
12. A restaurant had sold 3 times more honey roasted chicken than black pepper chicken.
If 90 less honey roasted chicken had been sold, the number of black pepper chicken
would have been twice the number of honey roasted chicken.
a) How many honey roasted chickens were sold?
b) How many black pepper chickens were sold?
Ans: _____________________[4]
13. If Andy buys 3 story books and 5 comic books, he will have $24 left. If he buys 5
story books and 3 comic books, he will need $16 more. Given that a comic book is
sold at $18, how much does Andy have?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-116-2048.jpg)
![14. In the figure below, 1, 2, 3, 4 and 5 are all squares. What is the ratio of the total area
of 1 and 2 to the total area of all the squares?
2 3 4 5
1 of the pupils like basketball,
11 3
Ans: _____________________[4]
15. Plastic tables were sold at $75 each and wooden tables were sold at $80 each. There
were 150 plastic tables in a shop at first. After selling all the tables, the shop received
$12850. How many wooden tables were sold?
Ans: _____________________[4]
16. In a class,
3
1 of the remainder like chess, the rest like
4
swimming. There are 10 pupils who like chess. Each pupil only likes one sport. What
is the number of pupils who like either chess or basketball?
Ans: _____________________[4]
1](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-117-2048.jpg)
![17. Mr. Wong hired a transport company to deliver some glass products for him. For
every safely transported product, the company charges $16.5. For every product that
was broken on the way, the company compensates $66. Mr. Wong was charged
$15,015 for the delivery. 90% of the products were delivered safely. How many
products were broken on the way?
11 4
Ans: _____________________[4]
18. Mindy and Ryan had an equal amount of cookies. Each day, Mindy ate 23 cookies
and Ryan ate 8 more cookies than Mindy.
a) How many days had passed when Mindy had 149 cookies left and Ryan had 53
cookies left?
b) How many cookies did each of them have at first?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-118-2048.jpg)









![For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. There are some flowers in a garden. 0.2 of the flowers are daisies and the remaining
5 of the roses are red and the rest are white. There are 24 more red
12 4
flowers are roses.
7
roses than white roses.
a) How many white roses are there?
b) How many daisies are there?
Ans: _____________________[4]
7. In the figure below, AB = BC = CA. FCD, BCE and ACG are straight lines. The
figure is not to scale. Find
a) ∠ CED
b) ∠ ACF
Ans: _____________________[4]
A
F
C
E
G
B
D
42o
31o](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-128-2048.jpg)
![8. Mrs. Foo bought 3.3 kg of fish at $1.59 per 100g, 2.8 kg of beef at $4.89 per 500 g,
and 7 packages of vegetable at $0.86 per package. How much did she pay for all the
goods?
12 5
Ans: _____________________[4]
9. The ratio of the number of curry puffs to the number of cakes in a shop is 1: 4. A
curry puff costs $2. Each cake is sold at $5. The total amount that the shop will
receive from selling all the cakes and curry puffs is $1892. How many cakes are
there?
Ans: _____________________[4]
10. A shop had 280 pens. 70% of the pens were blue. A week later, a number of blue
pens were sold and 60% of the remaining pens were blue. How many pens altogether
were there in the shop a week later?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-129-2048.jpg)
![11. A textbook and a bag cost $30. A textbook and a comic book cost $22.5. David
bought 4 textbooks, 2 bags and 1 comic book for $100. What is the cost of a comic
book?
12 6
Ans: _____________________[3]
12. Marion and Nina had some beads in the ratio 5: 7. If Marion gave Nina 24 beads,
Nina would have three times as many beads as Marion had. How many beads did
Marion have at first?
Ans: _____________________[4]
13. What fraction of 4l is 350ml? Express your answer in the simplest form.
Ans: _____________________[3]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-130-2048.jpg)
![14. 40% of the fruits in an orchard are apples, 80% of the remainder is oranges and the
rest are mangoes. There are 648 more oranges than apples. After some apples have
been sold, 10% of the remaining fruits in the basket are apples. How many apples
have been sold?
12 7
Ans: _____________________[4]
15. A salesman’s salary is $1575 a month. Apart from the salary, he earns a commission
of $1.20 for every $5 of sales he makes. In 8 months, the total sales he makes is
$72000. What is his average earning a month over these 8 months?
Ans: _____________________[4]
16. A rectangular tank measures 60 cm by 43 cm by 24 cm is filled with water up to
1
3
its height. At 1.p.m, water from a tap started to flow into the tank at a rate of 1.8 l per
minute. How much water is in the tank at 1.20 pm?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-131-2048.jpg)
![17. Three identical squares, each is made up of 9 identical squares, are overlapped as in
the figure below. Find the ratio of the shaded portion to the total area of the figure.
12 8
Ans: _____________________[4]
18. Joanne thinks of a number. The difference between thrice that number and of that
same number is 36 more than that number. What is the number that Joanne thinks of?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-132-2048.jpg)









![4. What is the average of the first 8 multiples of 9?
4 kg of meat and cooked
13 8
Ans: _____________________
5. Nicolas bought
5
7 kg for dinner. What is the quantity of
10
meat that has not been cooked? Give your answer in decimals.
Ans: _____________________
For Questions 6 to 18, show your workings clearly in the space provided for each
question and write your answers in the spaces provided. The number of marks awarded is
shown in brackets at the end of each question. (50 marks)
6. Mrs. Khoo mixed 6l grape syrup with 9l of water. After that, she used some
rectangular containers to store the drink. Each container measures 12 cm by 7 cm by
5 cm. Each container is filled completely.
a) How many containers could be filled?
b) What is the volume of the drink that was left over?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-142-2048.jpg)
![7. Find ∠ x in the figure below. AOB, COD, EOF are straight lines.
78o 33o
A B
13 9
Ans: _____________________[4]
8. In the figure below, the breadth of the rectangle is
3 its length. What is the area of
4
the shaded portion? The figure is not drawn to scale.
Ans: _____________________[4]
6.5 cm
17.5 cm
O
C
D
E
F
x](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-143-2048.jpg)
![9. Michael participated in a swimming competition. On average, he completed a lap in
3.2 minutes. He needed to swim 8 laps to complete the race. What was the total time
he took to complete the race? Give your answer in minutes and seconds.
14 0
Ans: _____________________[3]
10. A farmer planted 400 flowers in his garden.
5 of them were roses. The farmer then
8
sold some roses. The remaining number of roses was then
3 of the total number of
8
flowers remained in the garden. How many roses were sold?
Ans: _____________________[3]
11. The figure below is made up of two adjacent squares and a shaded triangle. The
smaller square has an area of 16 cm2. The larger square has an area of 49 cm2. What
is the area of the shaded triangle?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-144-2048.jpg)
![12. Find ∠z in the following figure. AOB and COD are straight lines. ∠y = ∠z. ∠x =
D
y z
1 hours on Monday. On Tuesday he spent some time to
14 1
12o. The figure is not to scale.
Ans: _____________________[4]
O
142o
x
13. Peter studied Physics for 2
2
continue his Physics study. On Wednesday, he spent twice as many hours as on
Tuesday to finish his Physics lesson. Over those 3 days, Peter spent an average of
138 minutes a day studying Physics. In how many hours did Peter study Physics on
Wednesday?
Ans: _____________________[4]
A
C B](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-145-2048.jpg)
![14. Jordan is a basketball player. On the first match of the 2009 league he scored 7 goals.
In every later match he scored 2 more goals than the previous match. He played 7
matches altogether in the league.
a) How many goals did he score in total?
b) What is his average number of goals per match?
15. Nelson’s height is 152 cm. Nelson’s sister is 0.2 m shorter than he is. What fraction
of Nelson’s height is his sister’s height? Express your answer in the simplest form.
14 2
Ans: _____________________[4]
16. In a volleyball tournament, there are 10 school teams. Each team has to play one
match against each of the other teams. How many matches will be played between
the teams?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-146-2048.jpg)
![17. Mr. Teo bought a table and two chairs for $300. The two chairs were sold at the
same price. The table’s price is twice as much as a chair’s. What is the price of the
table?
14 3
Ans: _____________________[4]
18. Peter wrote all the number from 1 to 100 continuously
1234567891011121314……979899100
How many digits did he write?
Ans: _____________________[4]](https://image.slidesharecdn.com/outreach-p5-math-141122165458-conversion-gate01/75/Outreach-p5-math-147-2048.jpg)

















