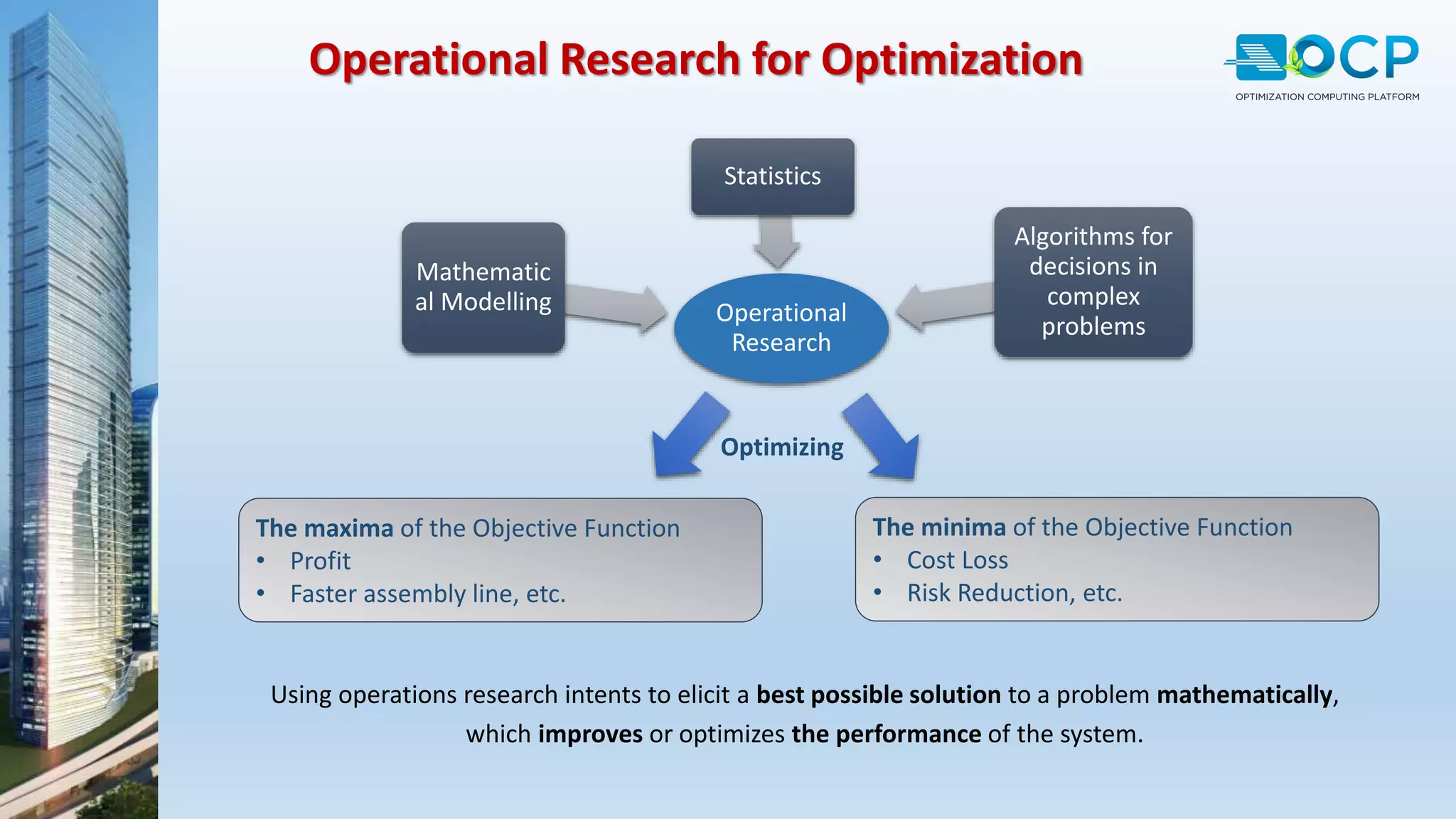
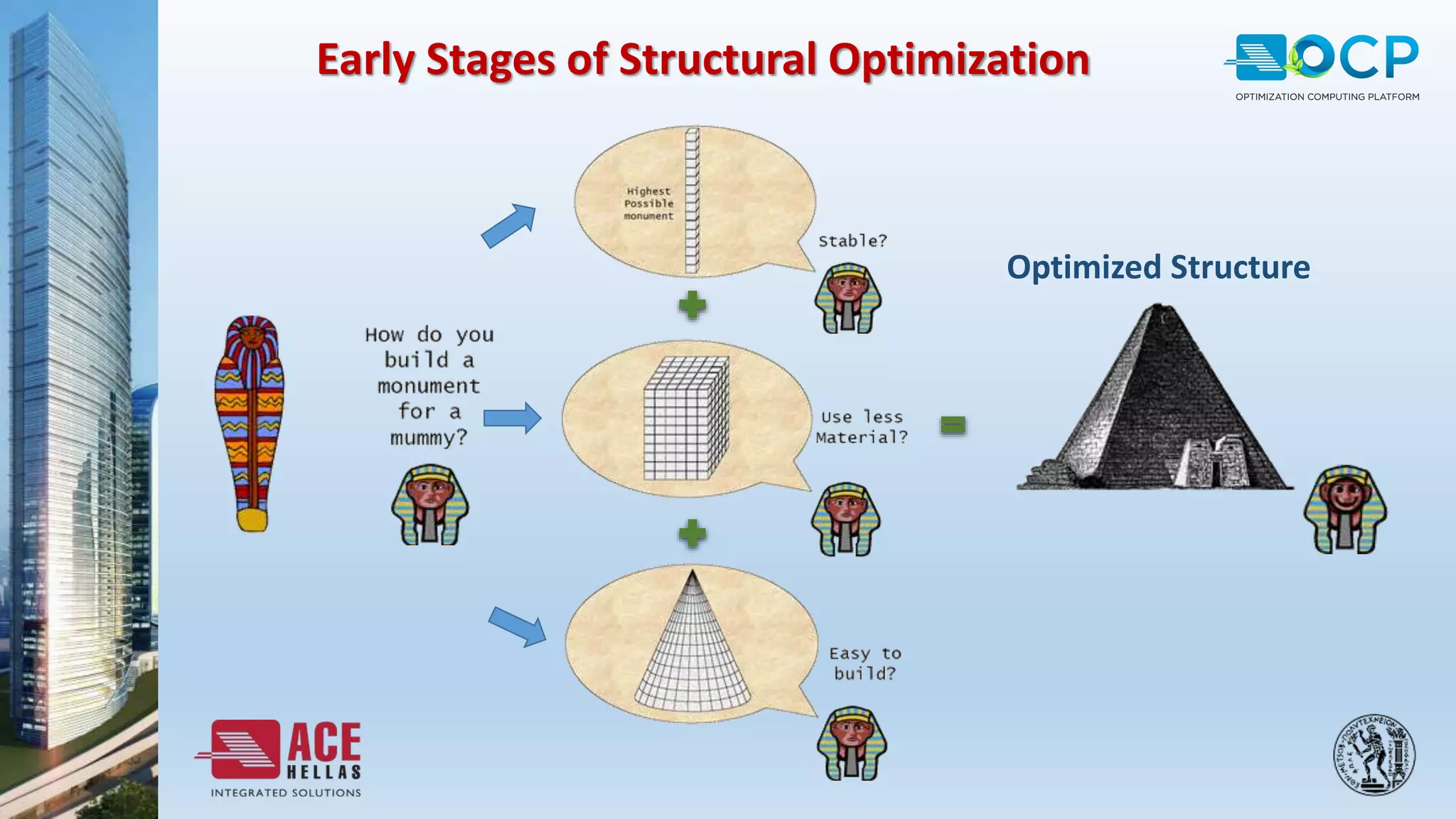
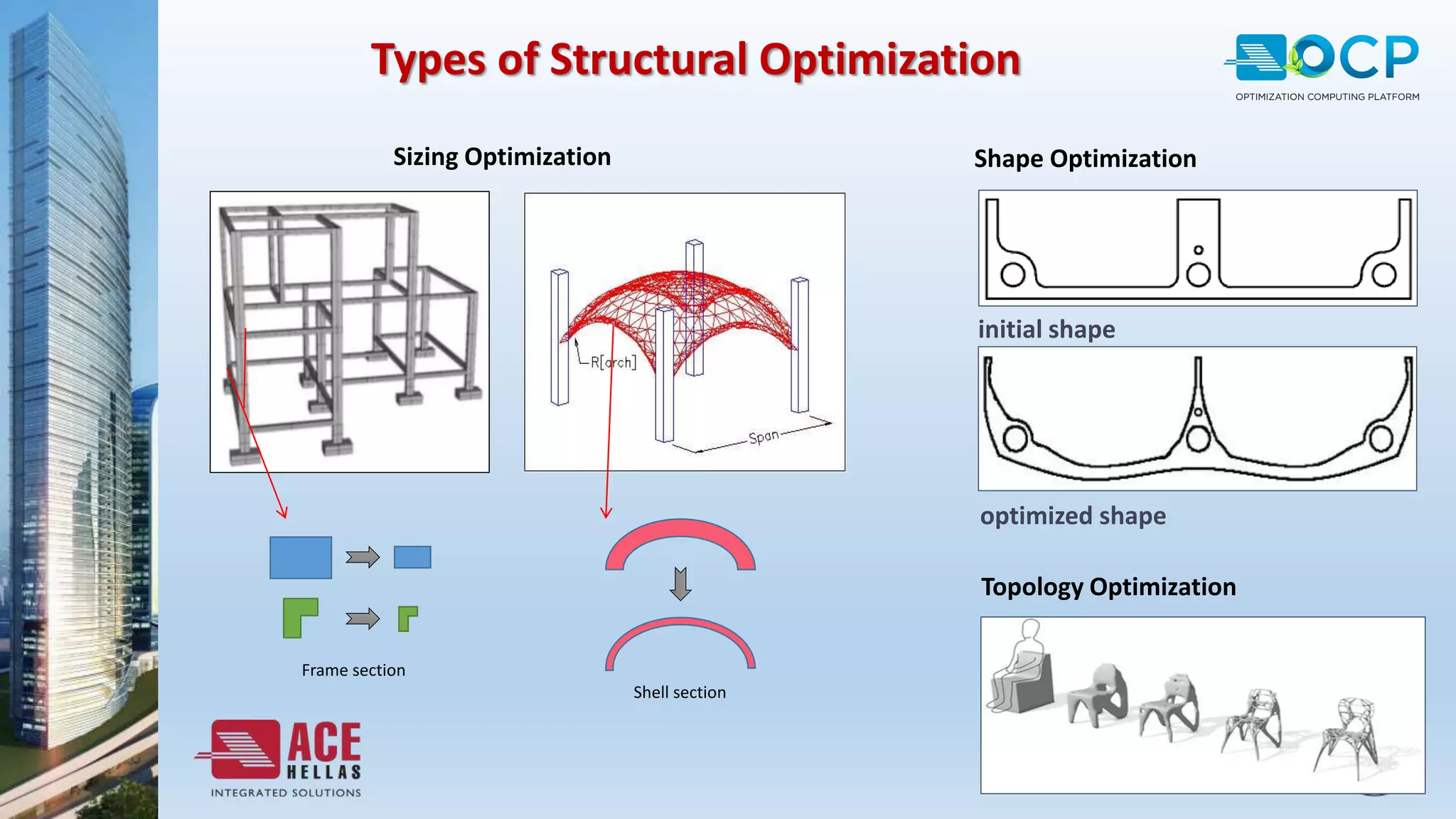
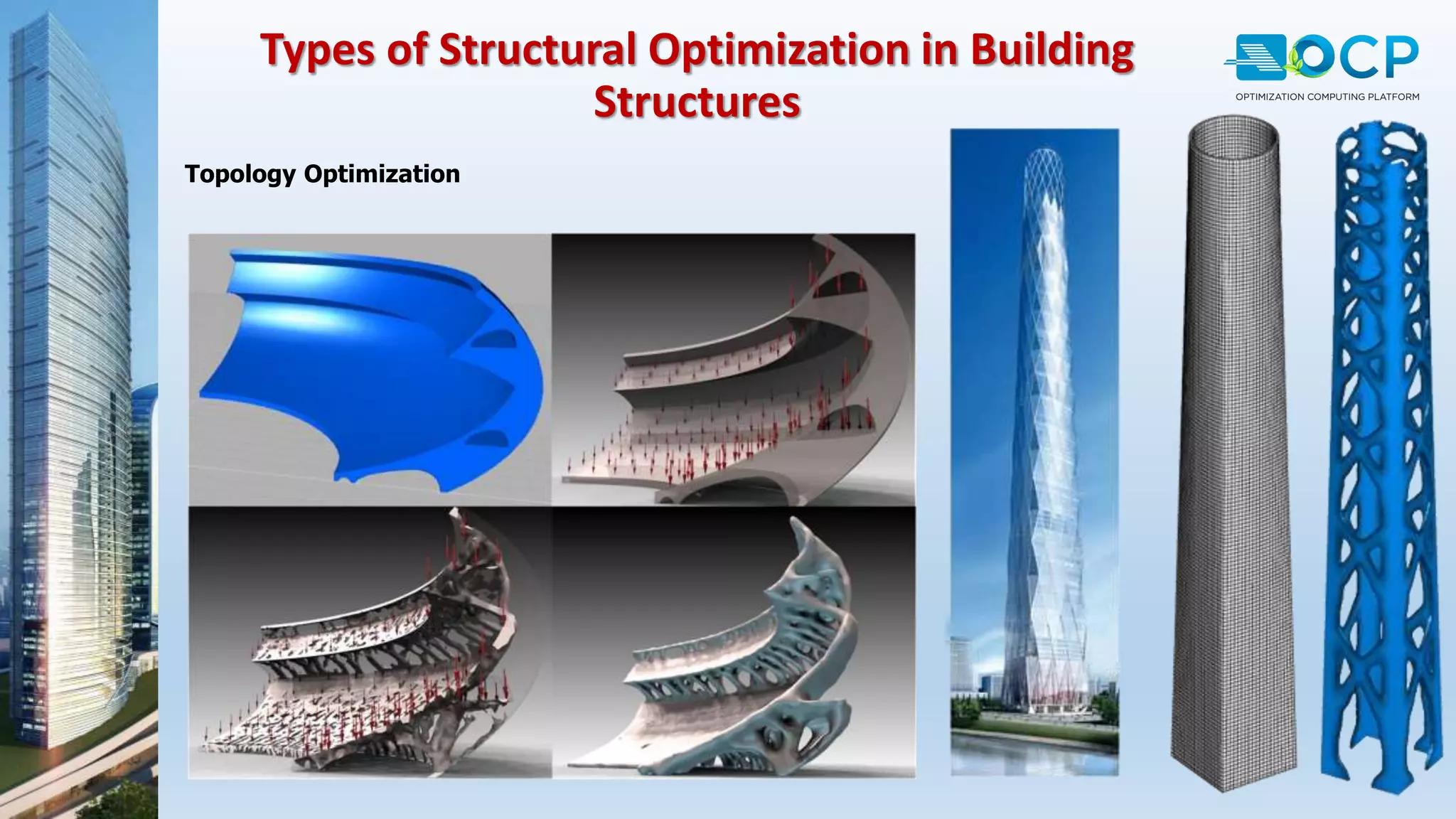
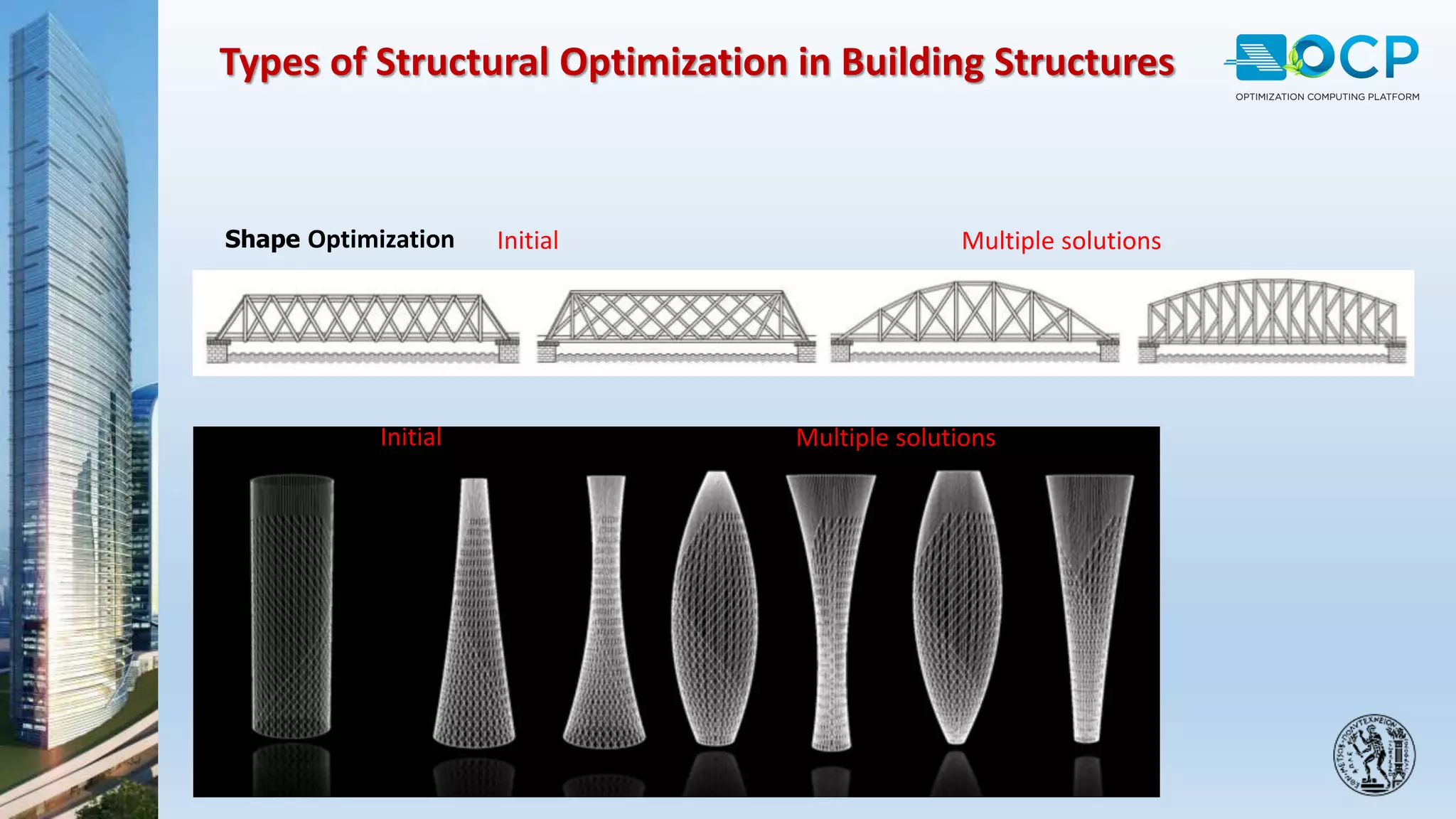
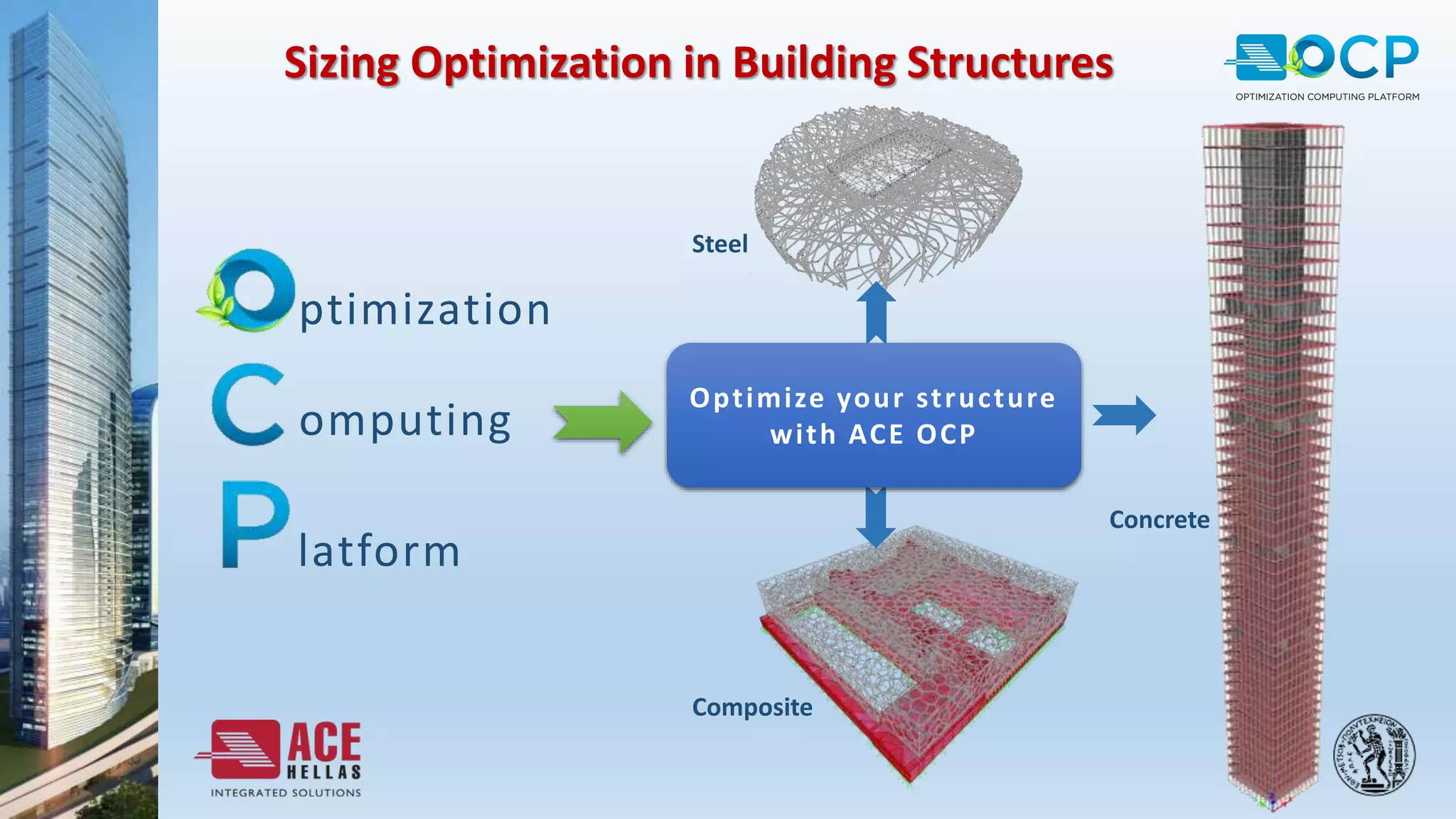
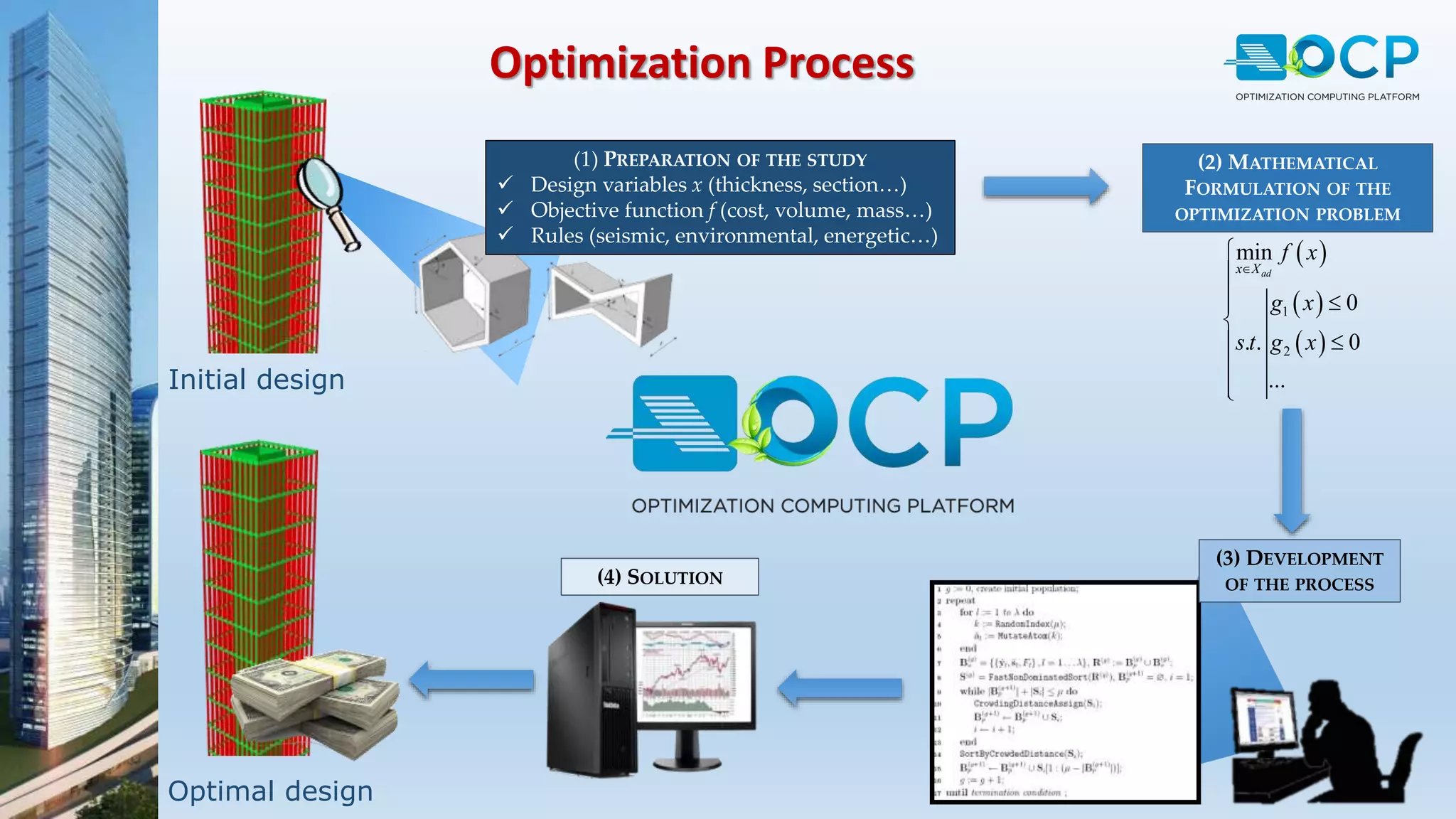
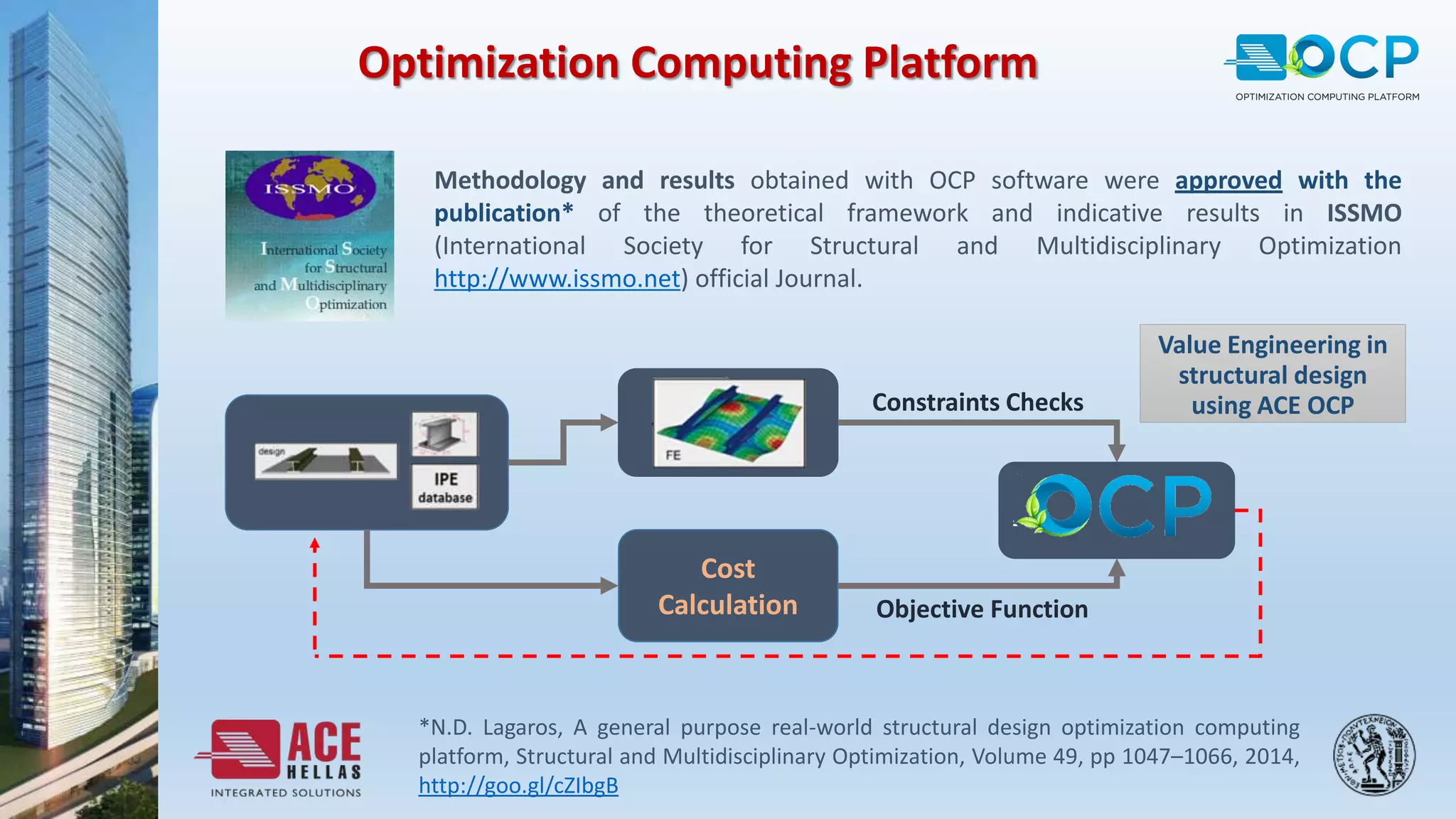
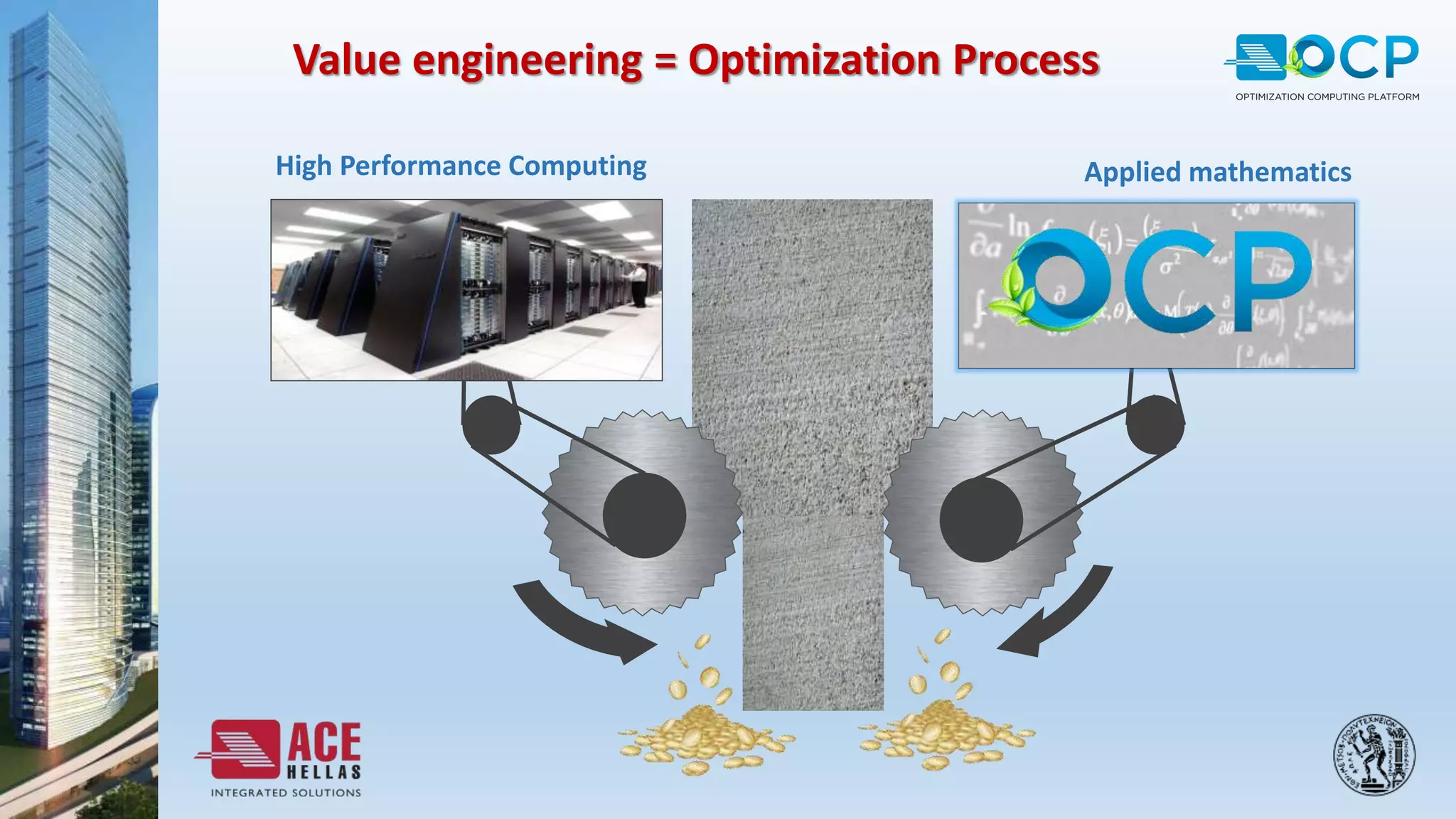
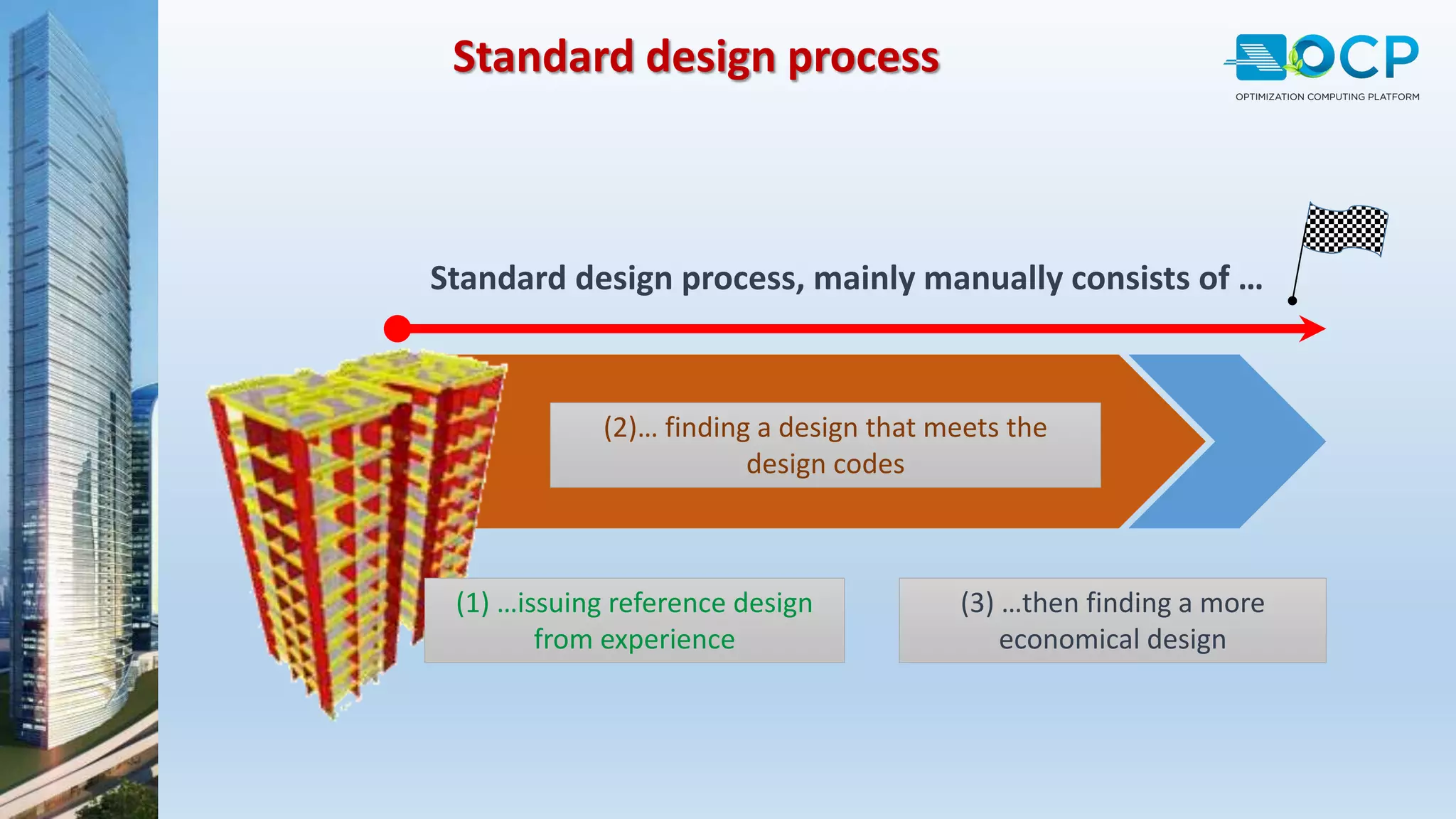
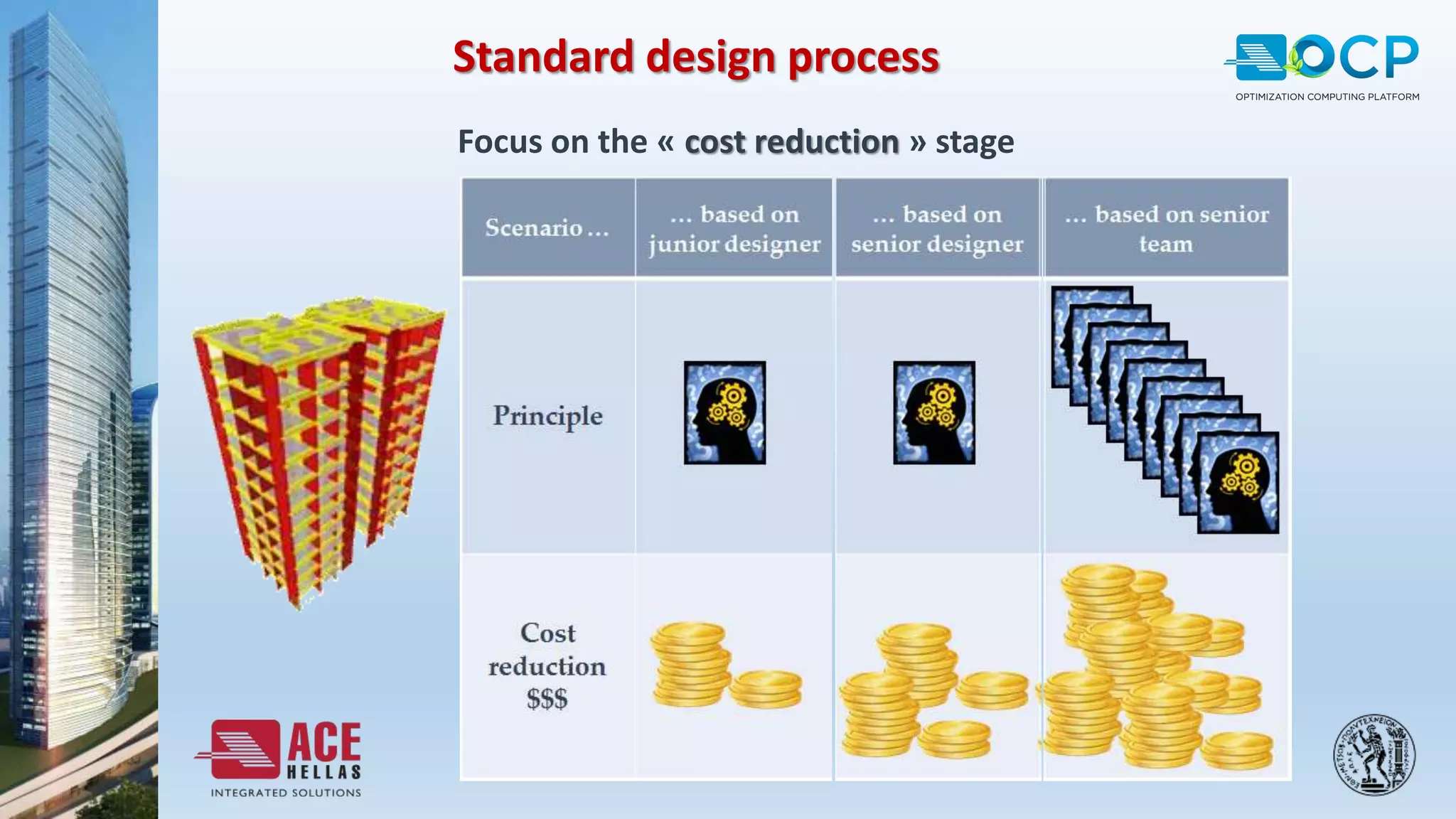
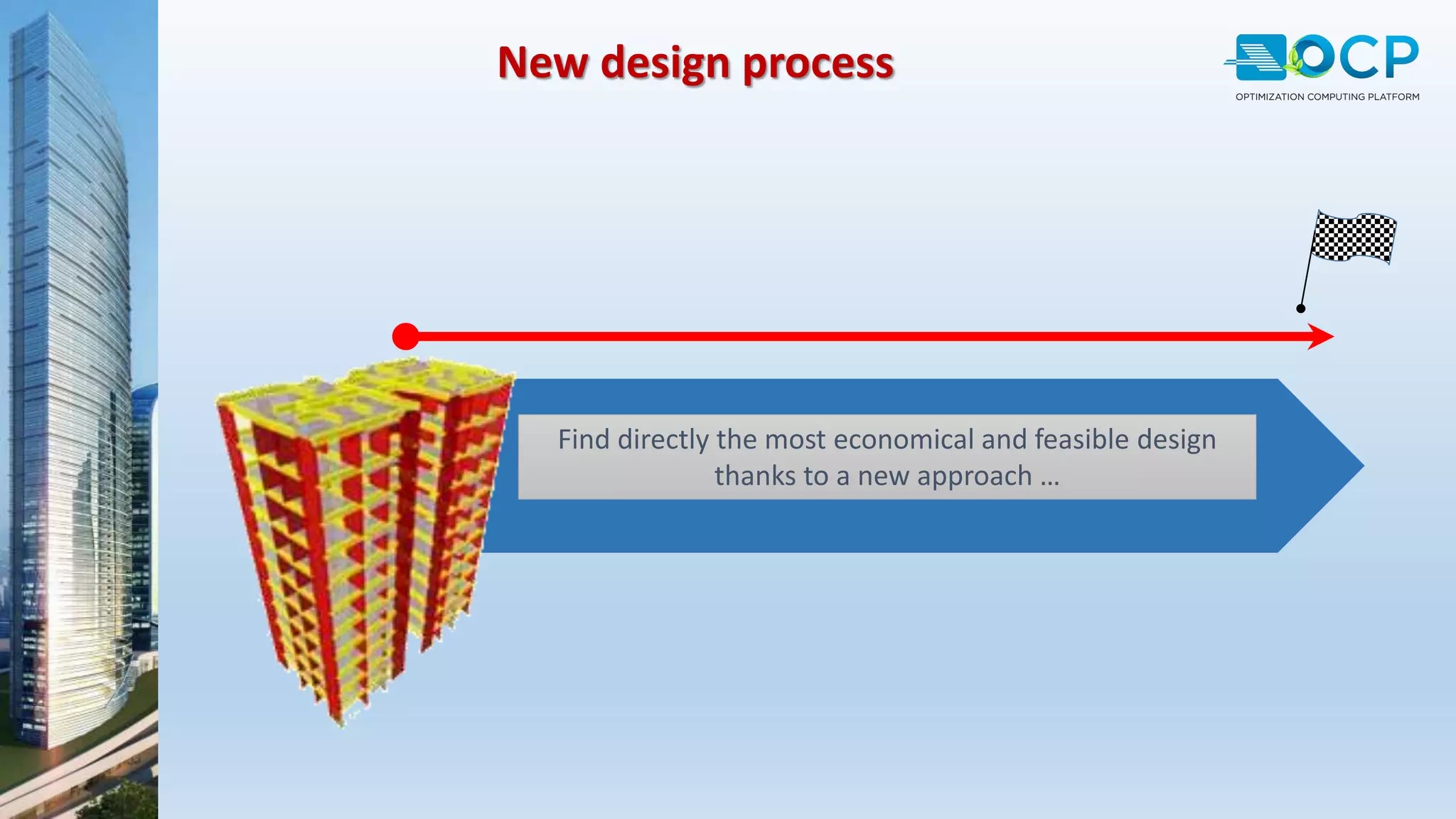
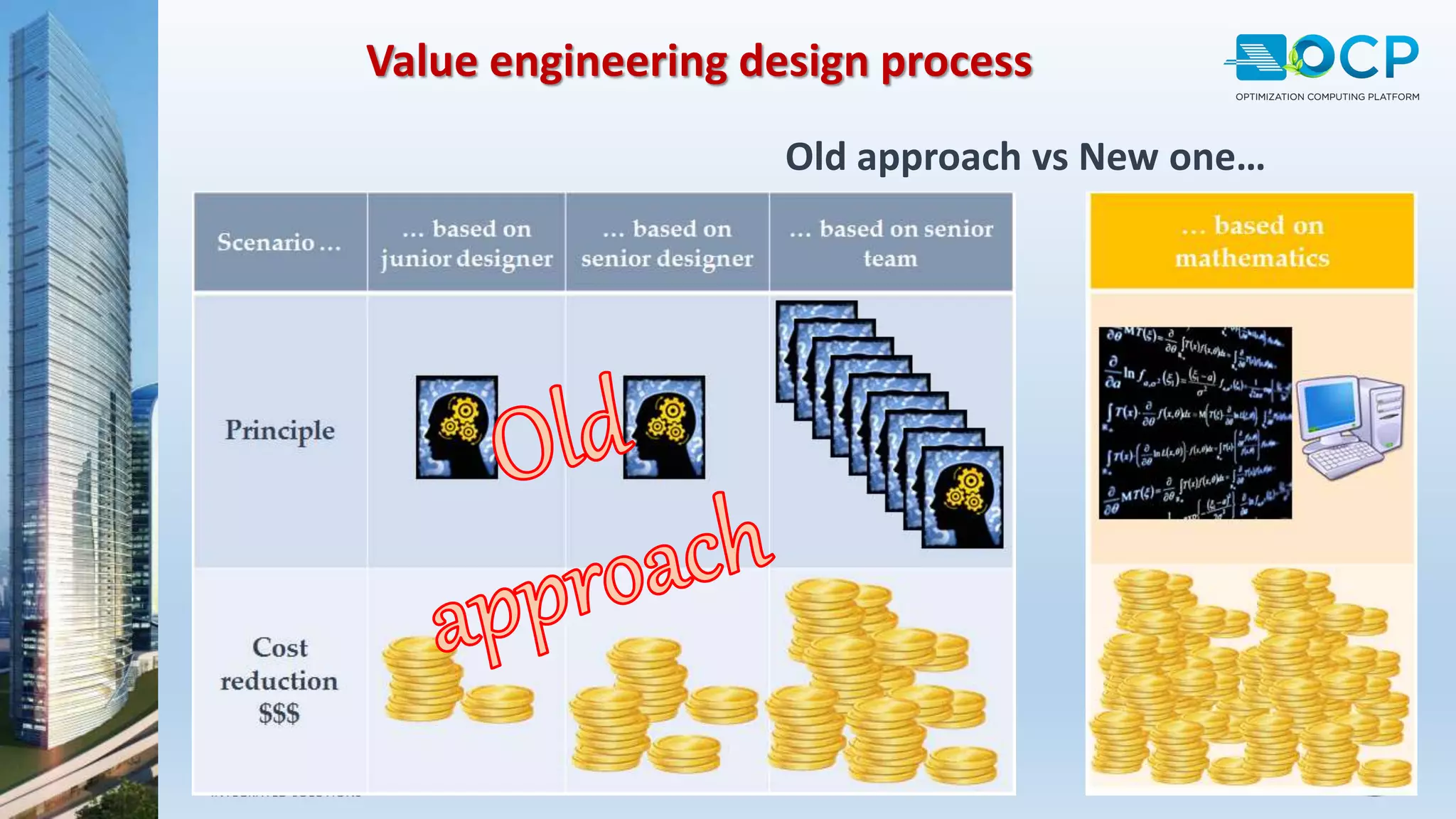
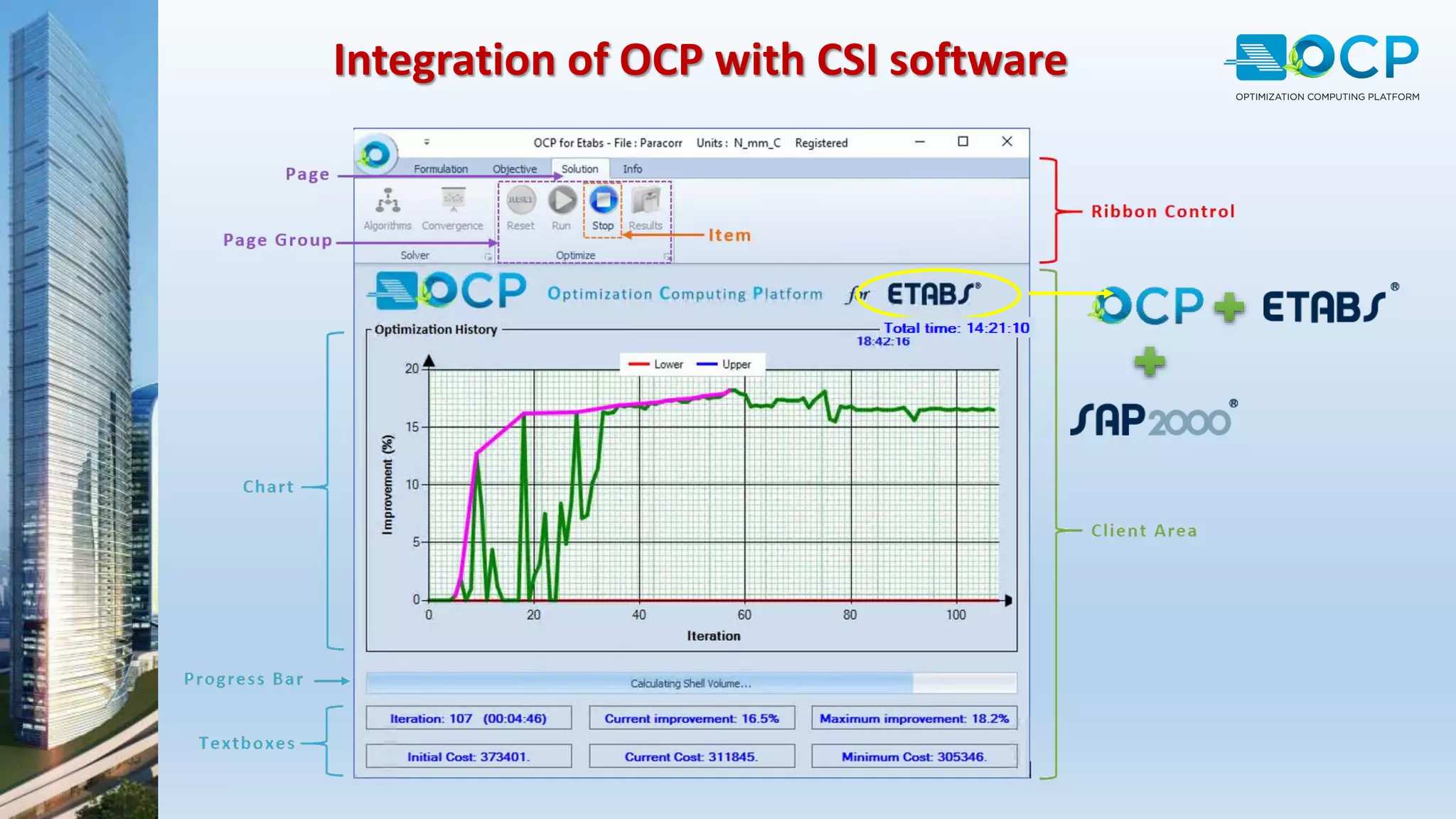
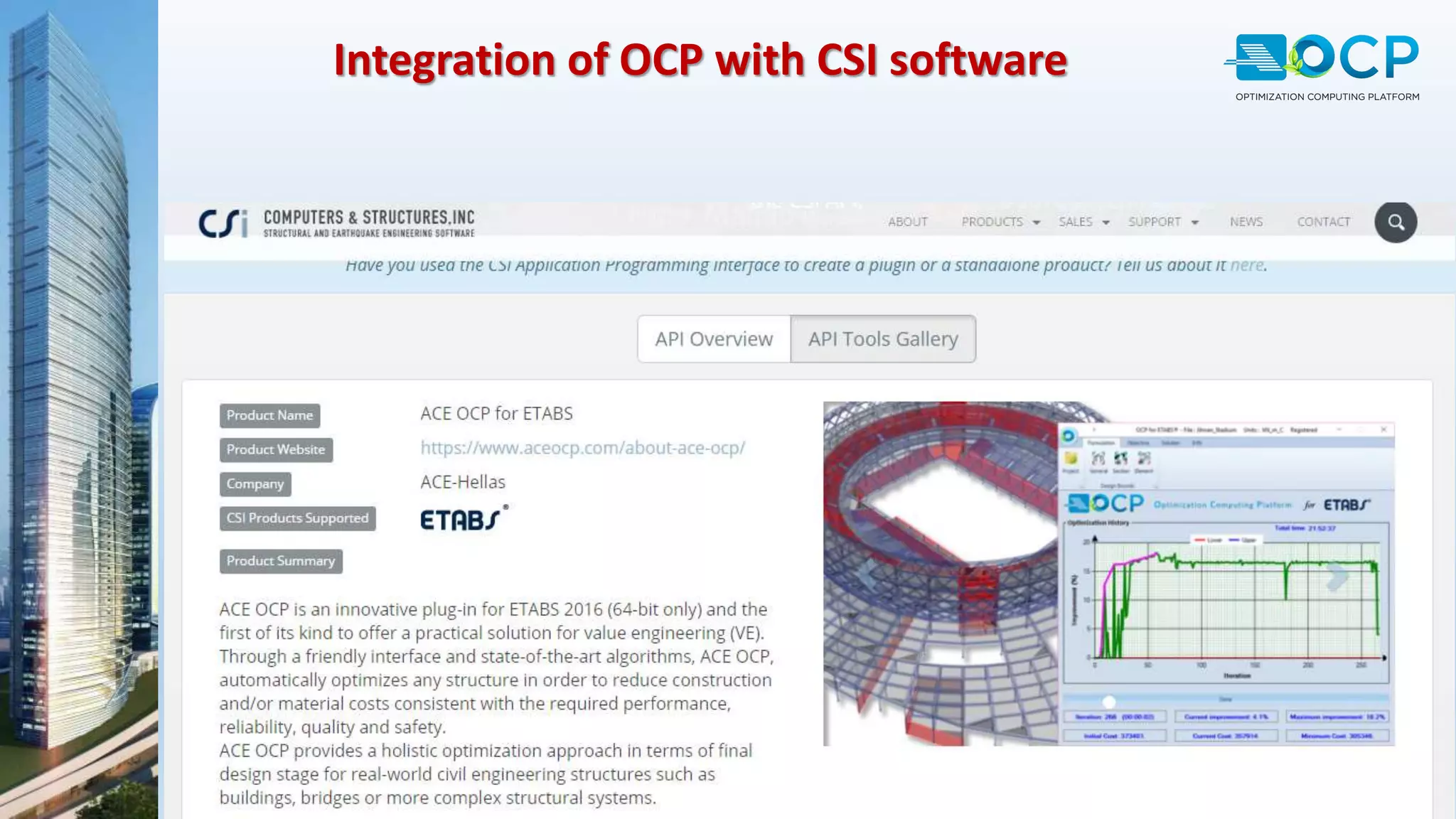
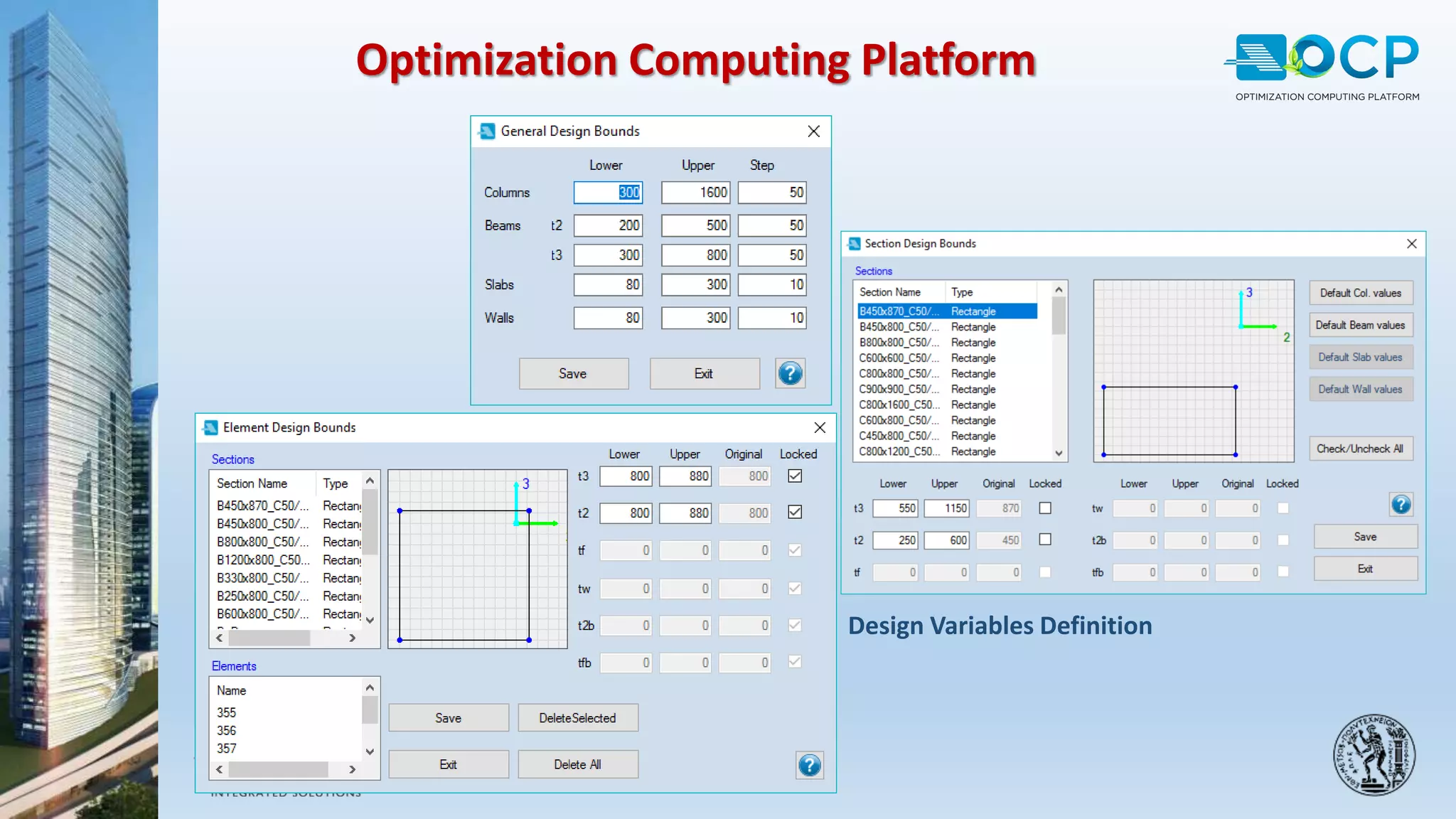
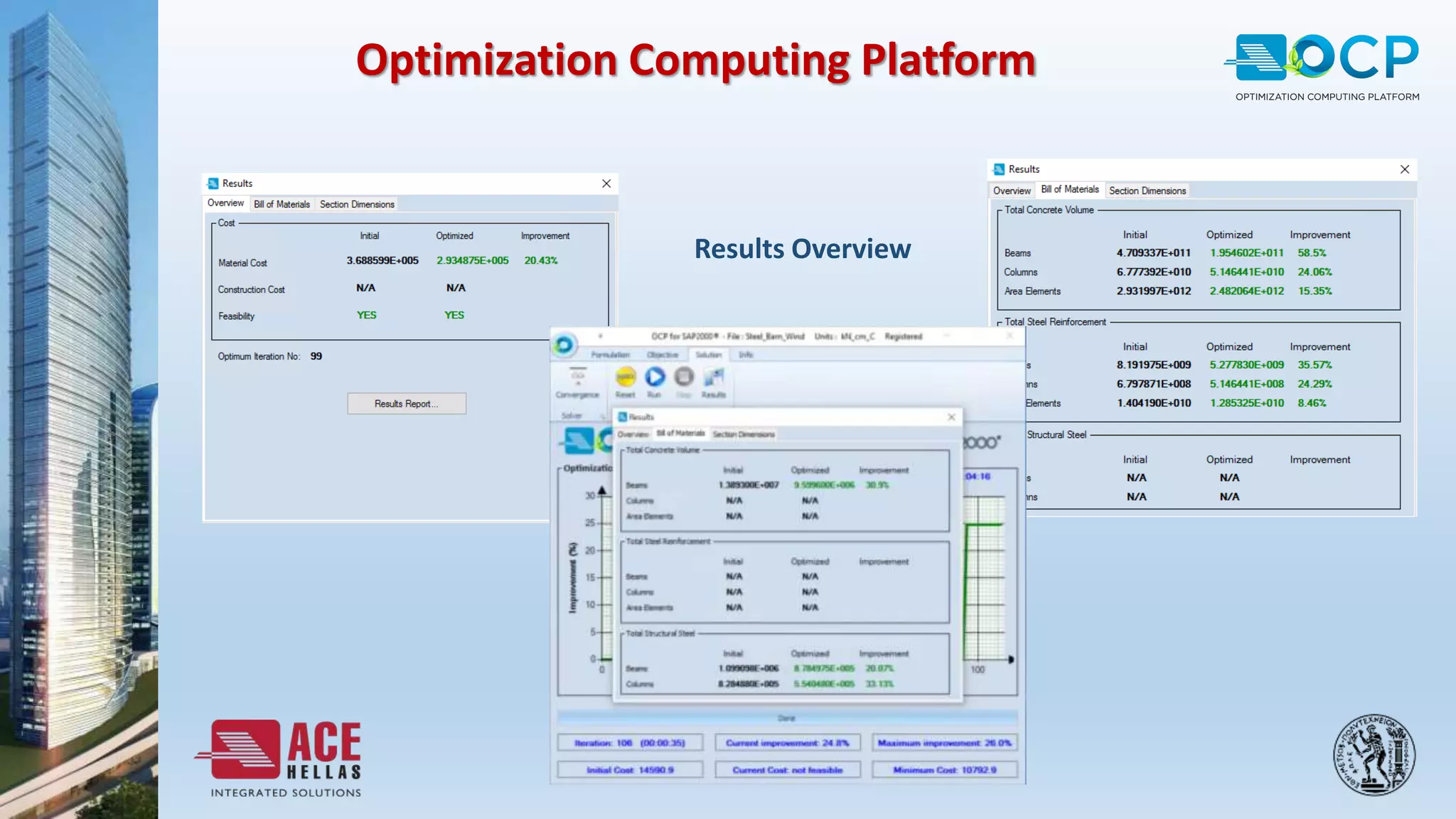
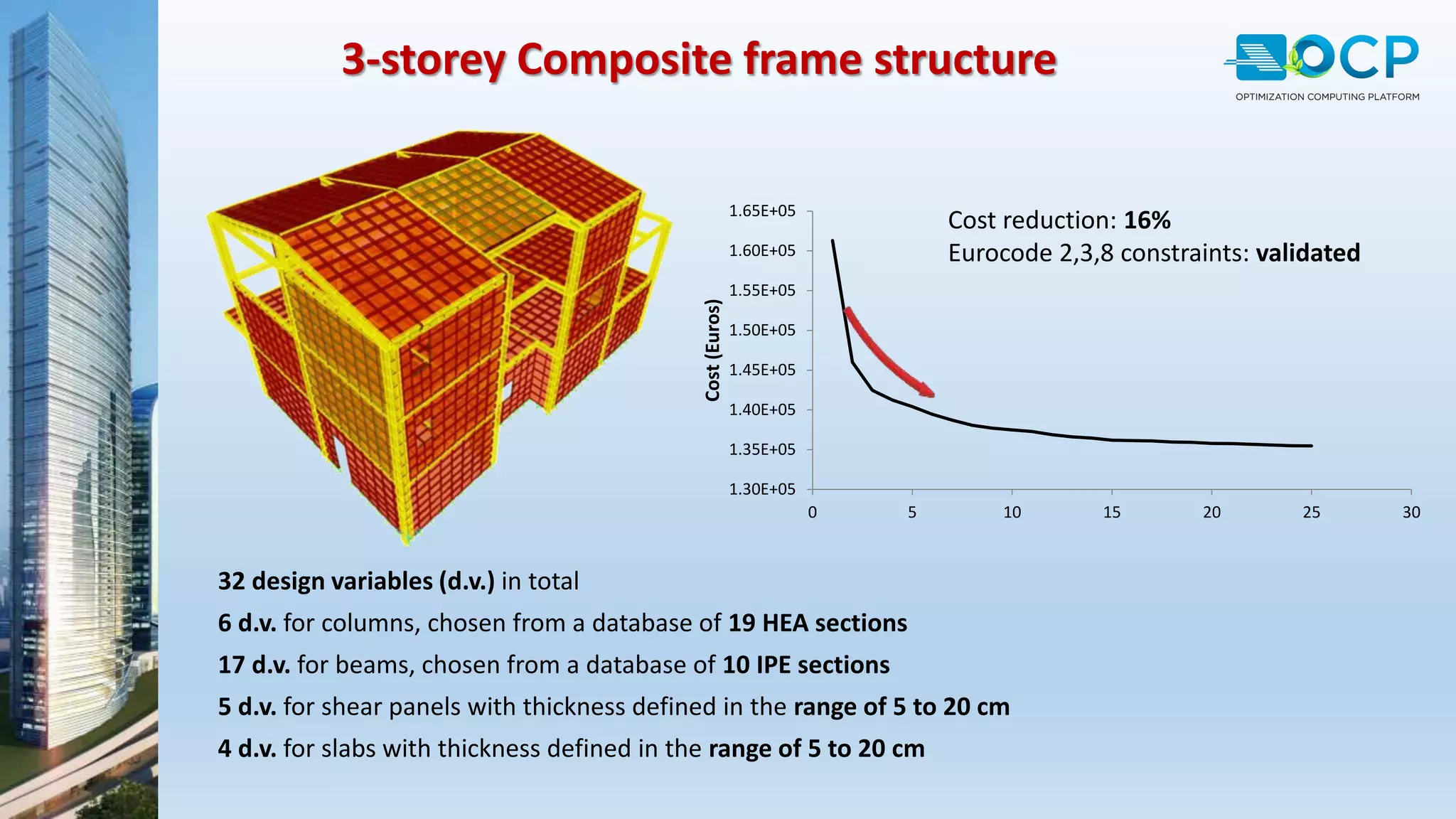
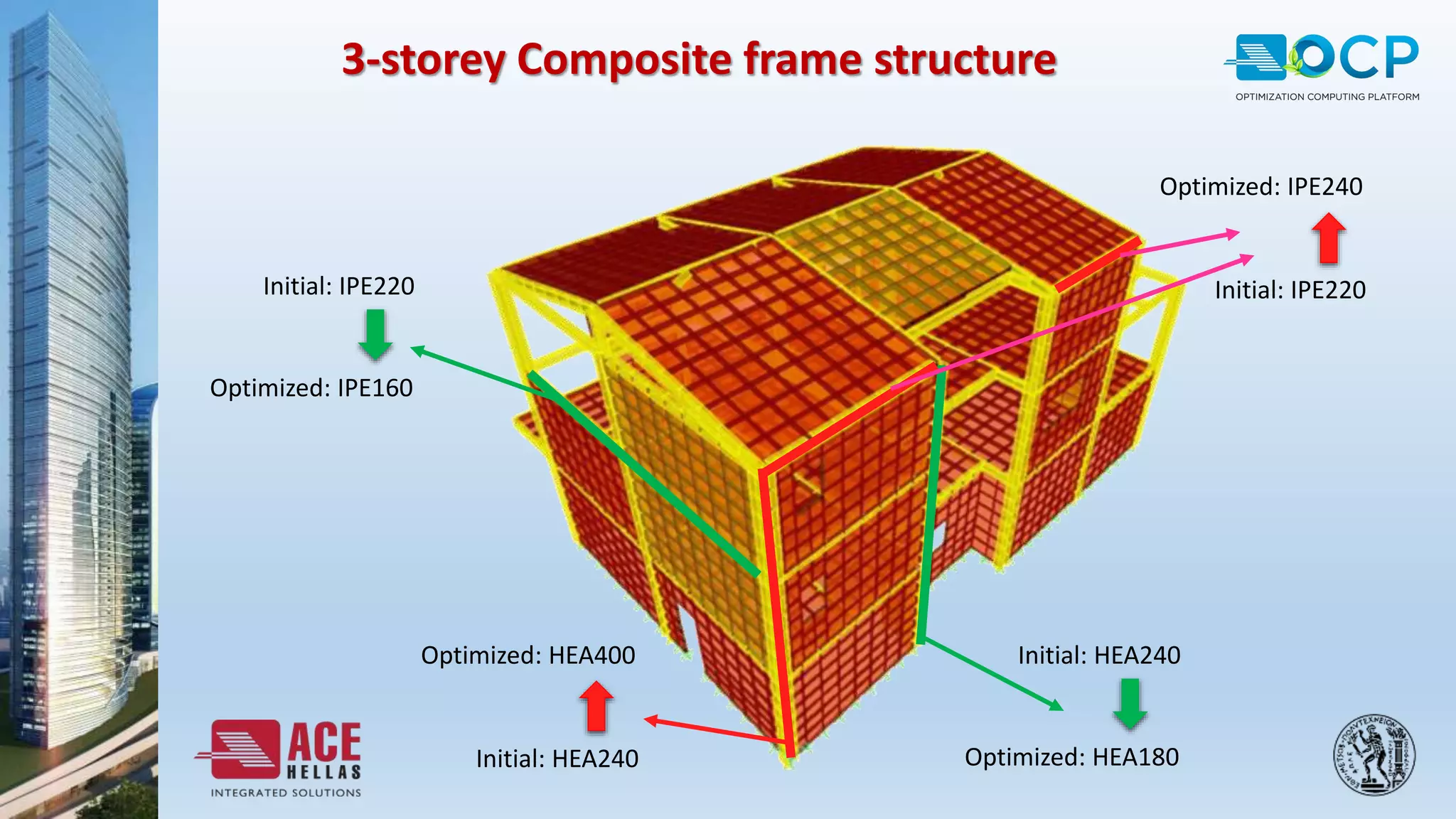
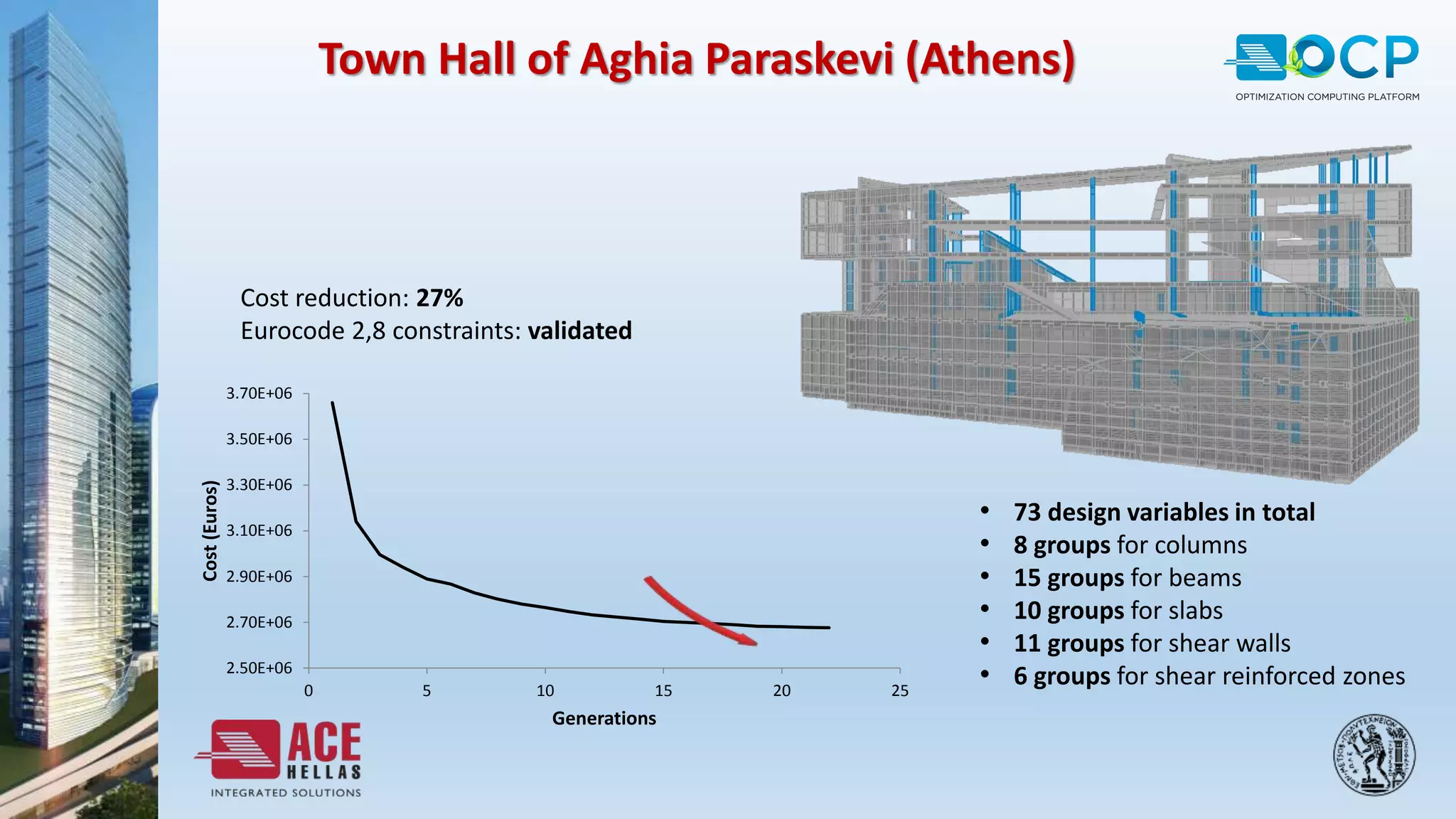
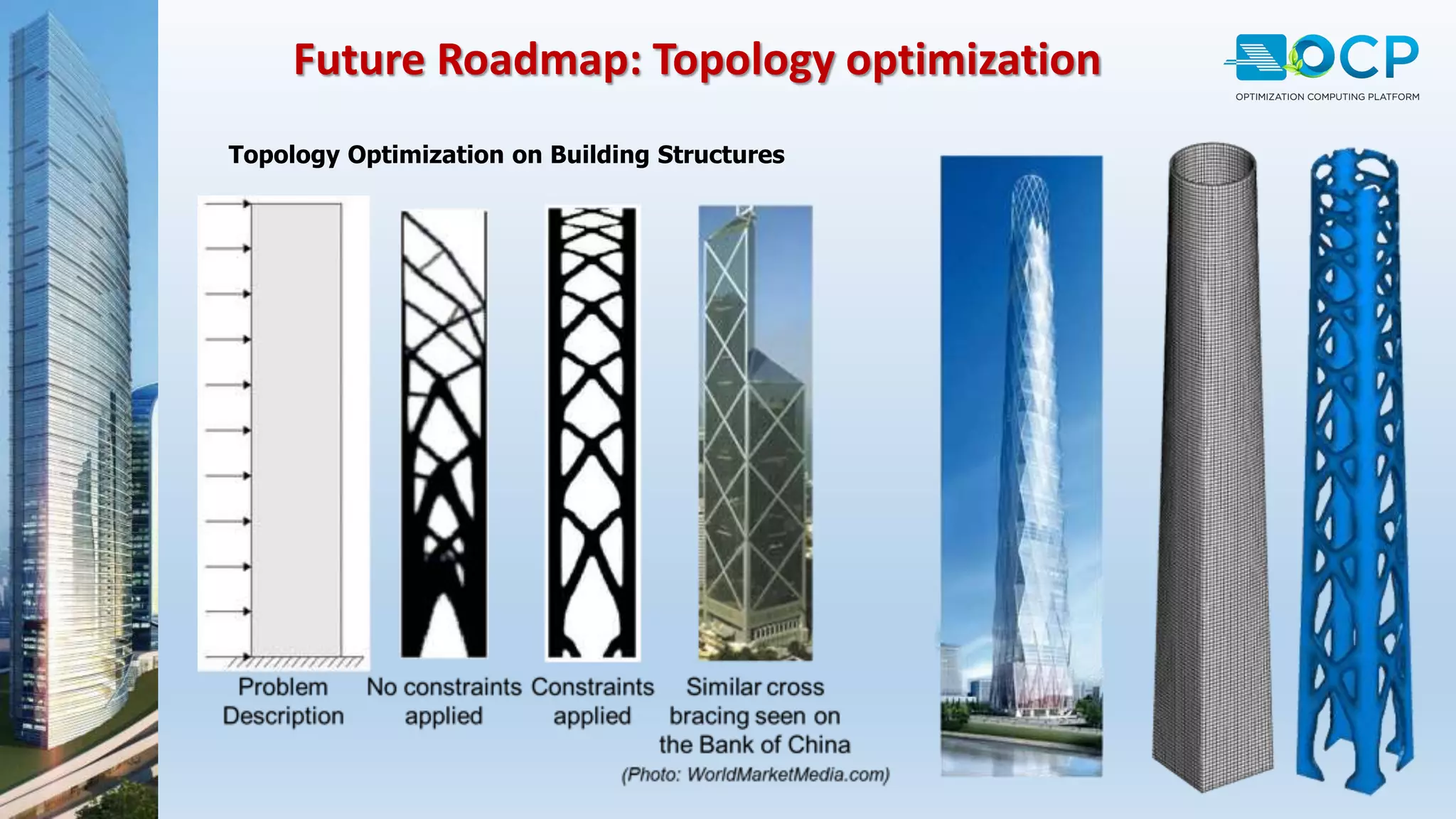
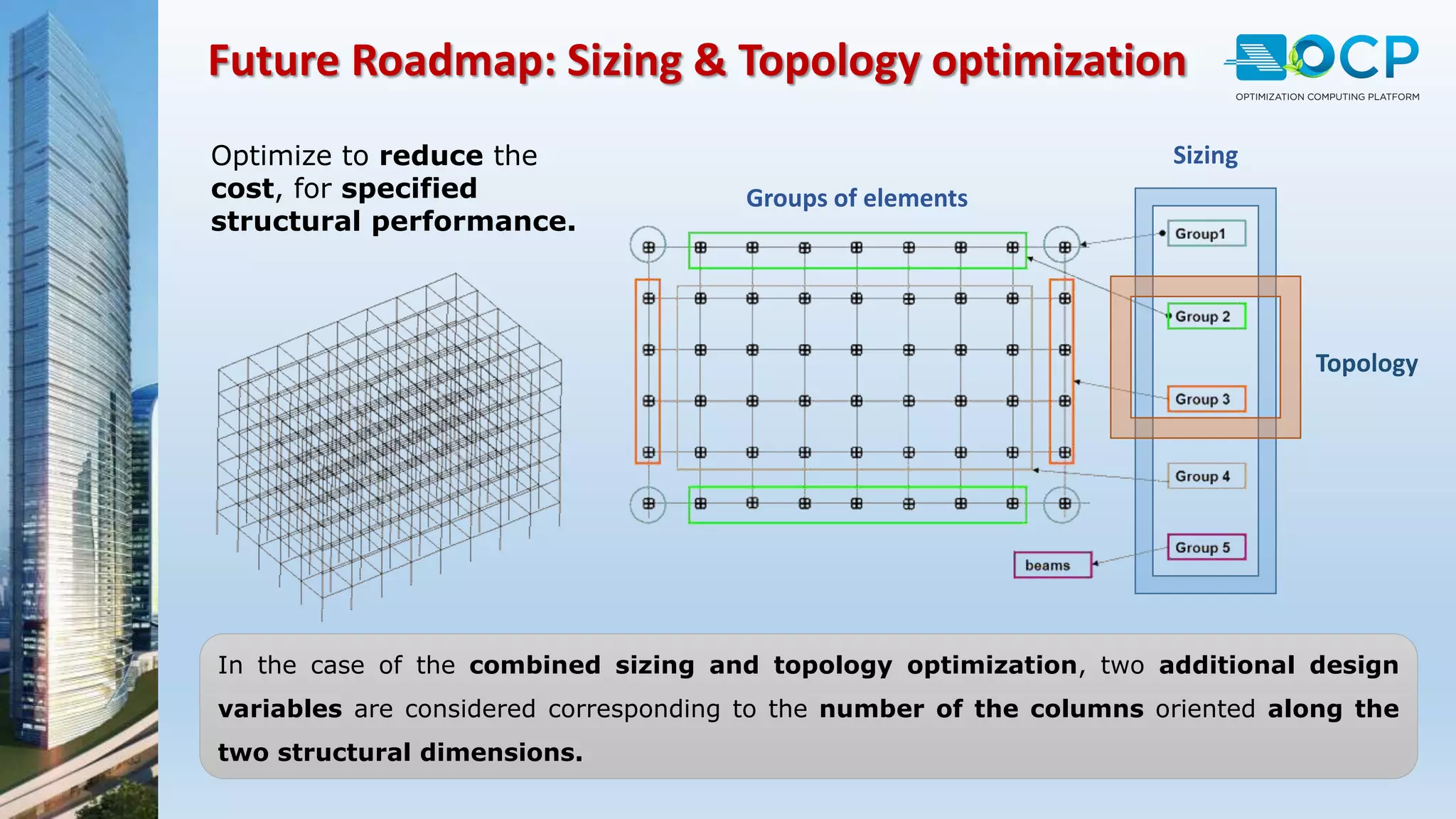
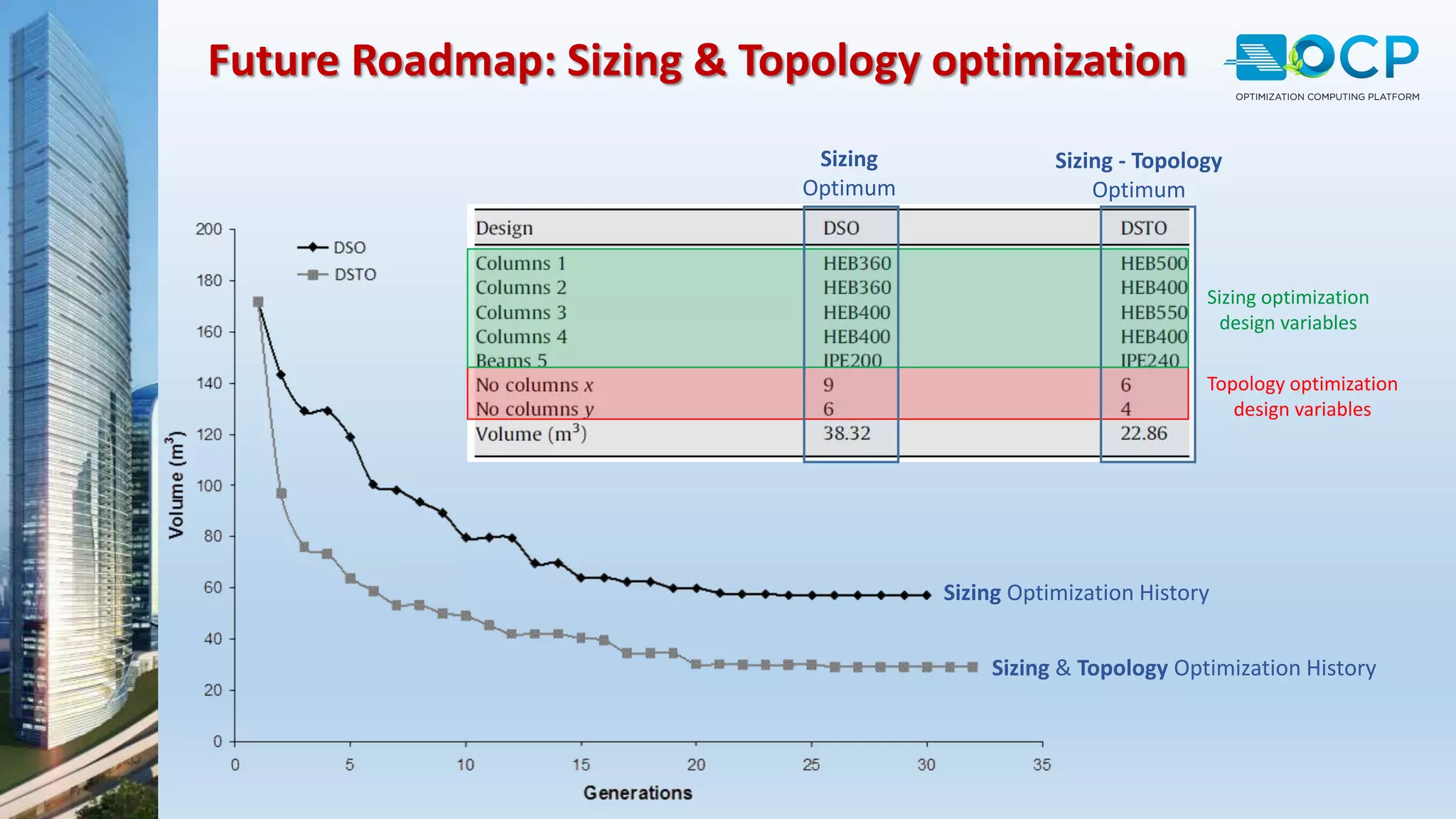
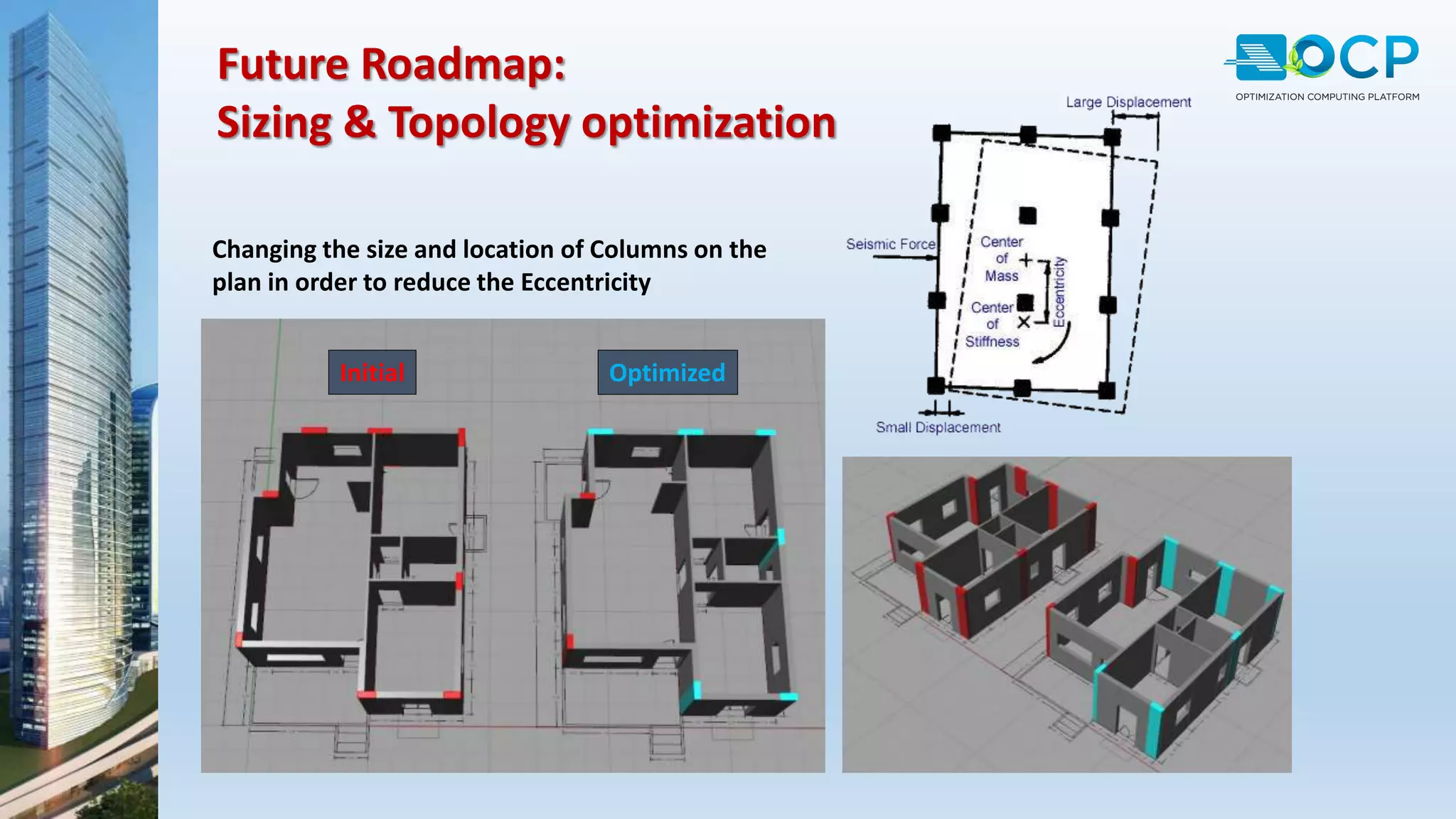
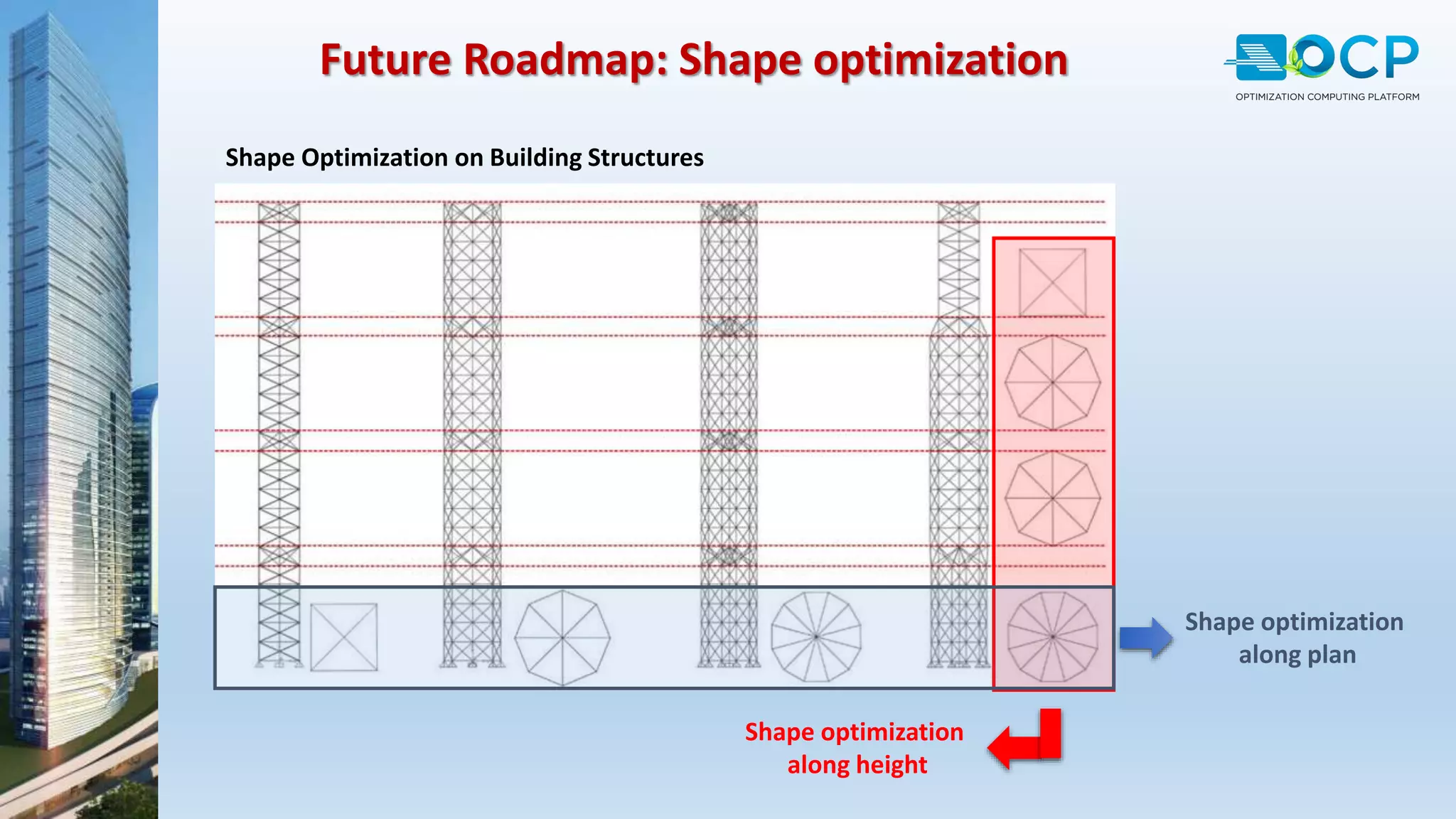
ACE-Hellas, a leader in technical software application development since 1979, focuses on structural design optimization through value engineering and operations research to minimize costs and maximize performance. The optimization process utilizes mathematical programming techniques to achieve the best structural solutions while integrating with various software for efficiency. The document outlines the historical development of optimization methods and presents case studies demonstrating significant cost reductions in building structures using ACE's optimization computing platform.

1. Structural Design Optimization
using ACE OCP

2. Brief History of ACE-Hellas
American Computers & Engineers SA (ACE-
Hellas), member of the Quest Group of
companies, was established in 1979 and is
today on of the largest integrated solution
providers in information technology and a
leader in technical software application
development.
A series of acquisitions, strategic partnerships
and investments have enabled ACE-Hellas to
become one of the fastest growing hi-tech
solution providers, with deep knowledge of the
Architecture, Engineering and Construction
(AEC) market, strong know how and solid
financial structure.

3. Less cost
Less waste
Less energy
Better safety
Better quality
Better performance
More value
More flexibility
More simplicity
Motivations for Value Engineering
To reduce the cost and increase the value by
applying optimization technologies!

4. What is optimization ?
• Optimization is the act of obtaining the best result under given circumstances.
• Optimization can be defined as the process of finding the conditions that give the maximum or
minimum of a function.
• The optimum seeking methods are also known as mathematical programming techniques and are
generally studied as a part of operations research.
• Operations research is a branch of mathematics concerned with the application of scientific methods
and techniques to decision making problems and with establishing the best or optimal solutions.
• Operations research (in the UK) or Operational research (OR) (in the US) is an interdisciplinary branch
of mathematics

5. Operational Research for Optimization
Operational
Research
Mathematic
al Modelling
Statistics
Algorithms for
decisions in
complex
problems
The maxima of the Objective Function
• Profit
• Faster assembly line, etc.
Using operations research intents to elicit a best possible solution to a problem mathematically,
which improves or optimizes the performance of the system.
Optimizing
The minima of the Objective Function
• Cost Loss
• Risk Reduction, etc.

6. • Isaac Newton (1642-1727)
(The development of differential calculus methods of optimization)
• Joseph-Louis Lagrange (1736-1813)
(Calculus of variations, minimization of functionals,
optimization for constrained problems)
• Augustin-Louis Cauchy (1789-1857)
(Solution by direct substitution, steepest descent method for unconstrained optimization)
• Leonhard Euler (1707-1783)
(Calculus of variations, minimization of functionals)
• Gottfried Leibnitz (1646-1716)
(Differential calculus methods of optimization)
Historical Development

7. • George Bernard Dantzig (1914-2005)
(Linear programming and Simplex method (1947))
• Richard Bellman (1920-1984)
(Principle of optimality in dynamic programming problems)
• Harold William Kuhn (1925-)
(Necessary and sufficient conditions for the optimal solution of programming
problems, game theory)
• Albert William Tucker (1905-1995)
(Necessary and sufficient conditions for the optimal solution of programming
problems, nonlinear programming, game theory: his PhD student was John Nash)
• Von Neumann (1903-1957) (game theory)
Historical Development

8. Early Stages of Structural Optimization
Optimized Structure

9. Types of Structural Optimization
Sizing Optimization Shape Optimization
initial shape
optimized shape
Topology Optimization
Shell section
Frame section

10. Types of Structural Optimization in Building
Structures
Topology Optimization

11. Shape Optimization
Initial Multiple solutions
Multiple solutionsInitial
Types of Structural Optimization in Building Structures

12. Sizing Optimization in Building Structures
ptimization
omputing
latform
Optimize your structure
with ACE OCP
Composite
Steel
Concrete

13. (2) MATHEMATICAL
FORMULATION OF THE
OPTIMIZATION PROBLEM
(4) SOLUTION
Initial design
Optimal design
 
 
 
1
2
min
0
. . 0
...
adx X
f x
g x
s t g x



 




(1) PREPARATION OF THE STUDY
 Design variables x (thickness, section…)
 Objective function f (cost, volume, mass…)
 Rules (seismic, environmental, energetic…)
(3) DEVELOPMENT
OF THE PROCESS
Optimization Process

14. Optimization Computing Platform
Methodology and results obtained with OCP software were approved with the
publication* of the theoretical framework and indicative results in ISSMO
(International Society for Structural and Multidisciplinary Optimization
http://www.issmo.net) official Journal.
*N.D. Lagaros, A general purpose real-world structural design optimization computing
platform, Structural and Multidisciplinary Optimization, Volume 49, pp 1047–1066, 2014,
http://goo.gl/cZIbgB
Value Engineering in
structural design
using ACE OCP
Cost
Calculation
Constraints Checks
Objective Function

15. Value engineering = Optimization Process
Applied mathematicsHigh Performance Computing

16. Why use ACEOCP?
GAIN
COST

17. How to reach the cheapest design
while meeting all the design rules

18. Standard design process, mainly manually consists of …
(2)… finding a design that meets the
design codes
(3) …then finding a more
economical design
(1) …issuing reference design
from experience
Standard design process

19. Focus on the « cost reduction » stage
Standard design process

20. New Approach

21. New design process
Find directly the most economical and feasible design
thanks to a new approach …

22. Old approach vs New one…
Value engineering design process

23. Integration of OCP with CSI software

24. Integration of OCP with CSI software

25. Design Variables Definition
Optimization Computing Platform

26. Cost Values per Material
Registration Form
Optimization Computing Platform

27. Results Overview
Optimization Computing Platform

28. Reinforced Concrete Sections Structural Steel Sections
Optimization Computing Platform

29. 1.30E+05
1.35E+05
1.40E+05
1.45E+05
1.50E+05
1.55E+05
1.60E+05
1.65E+05
0 5 10 15 20 25 30
Cost(Euros)
Generations
Cost reduction: 16%
Eurocode 2,3,8 constraints: validated
3-storey Composite frame structure
32 design variables (d.v.) in total
6 d.v. for columns, chosen from a database of 19 HEA sections
17 d.v. for beams, chosen from a database of 10 IPE sections
5 d.v. for shear panels with thickness defined in the range of 5 to 20 cm
4 d.v. for slabs with thickness defined in the range of 5 to 20 cm

30. Optimized: IPE160
Initial: IPE220
Optimized: HEA180
Initial: HEA240Optimized: HEA400
Initial: HEA240
Optimized: IPE240
Initial: IPE220
3-storey Composite frame structure

31. 2.50E+06
2.70E+06
2.90E+06
3.10E+06
3.30E+06
3.50E+06
3.70E+06
0 5 10 15 20 25
Cost(Euros)
Generations
Cost reduction: 27%
Eurocode 2,8 constraints: validated
Town Hall of Aghia Paraskevi (Athens)
• 73 design variables in total
• 8 groups for columns
• 15 groups for beams
• 10 groups for slabs
• 11 groups for shear walls
• 6 groups for shear reinforced zones

32. Bird’s Nest
Water Cube
Beijing 2008 Olympic Games
Description
• 98 design variables
• Regulation: BS5950 codes
• Cost reduction : 7%
Description
•139 design variables
• Regulation: AISC-ASD codes
• Cost reduction : 10%

33. 78000
80000
82000
84000
86000
88000
90000
92000
94000
96000
initial design final design
m3
-10%
Results on DUBAI Skyscraper
The problem consists of:
1. finding the cheapest design
2. while meeting some constraints
(i.e. displacement at the top level)
Our process of optimization is iterative and
leads to the cheapest feasible solution.
Red sections  enlarged
Green sections  reduced
Volume reduction: 10%
Displacement constraint : validated
(Maximum displacement= 997mm)

34. Multidisciplinary
Optimization
Future Roadmap: Sizing optimization

35. Topology Optimization on Building Structures
Future Roadmap: Topology optimization

36. Future Roadmap: Sizing & Topology optimization
In the case of the combined sizing and topology optimization, two additional design
variables are considered corresponding to the number of the columns oriented along the
two structural dimensions.
Sizing
Topology
Groups of elements
Optimize to reduce the
cost, for specified
structural performance.

37. Topology optimization
design variables
Sizing optimization
design variables
Sizing Optimization History
Sizing & Topology Optimization History
Sizing
Optimum
Sizing - Topology
Optimum
Future Roadmap: Sizing & Topology optimization

38. Changing the size and location of Columns on the
plan in order to reduce the Eccentricity
Initial Optimized
Future Roadmap:
Sizing & Topology optimization

39. Shape Optimization on Building Structures
Future Roadmap: Shape optimization
Shape optimization
along plan
Shape optimization
along height

40. Thank You
www.aceocp.com
www.ace-hellas.com
info@aceocp.com
Set a goal to decrease your
customer’s model by 9% to 13%…
…let ACE-Hellas’ Optimization Computing
Platform show you how.