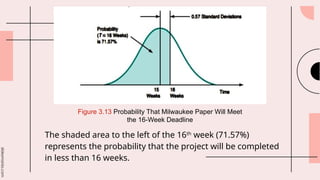
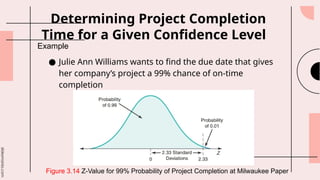
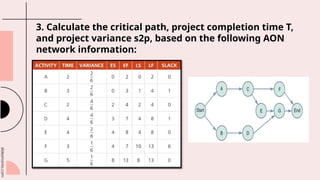
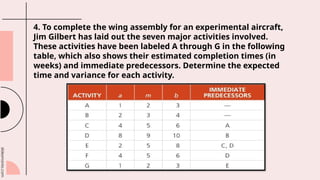
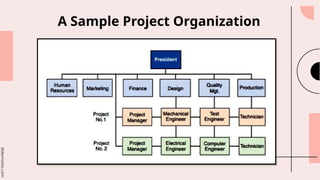
This document outlines the fundamentals of project management, including planning, scheduling, and controlling projects through techniques like PERT and CPM. It emphasizes the importance of effective project management in ensuring timely, budget-compliant, and quality project completion while discussing risk mitigation and resource management. Additionally, it covers topics such as critical path analysis, project variability, cost-time trade-offs, and project crashing to meet tight deadlines.




































![slidesmania.com
ty Distribution
with Three Time Estimates
● To find the expected activity time,
t, the beta distribution weights the
three time estimates as follows:
t = (a + 4m + b) 6
∕
● To compute the dispersion or
variance of activity completion
time, we use the formula:1
Variance = [(b a) 6]2
− ∕
Figure 3.11 Beta Probability Distribution
with Three Time Estimates](https://image.slidesharecdn.com/operationsmanagementprojectmanagement-241001101505-f298dc9d/85/Operations-Management-Project-Management-pptx-43-320.jpg)