The document discusses alpha cuts and their properties in fuzzy sets. It defines alpha cuts as crisp sets containing elements of the universal set whose membership degree in the fuzzy set is greater than or equal to alpha. The higher the alpha value, the smaller the alpha cut set. It also discusses support, core, and height of fuzzy sets. Support is the crisp set of all elements with non-zero membership, core those with membership 1, and height the highest alpha value of a non-empty alpha cut. Examples are given to illustrate key fuzzy set operations and concepts.

1. OPERASI PADA HIMPUNAN SAMAR; ALPHA CUT DAN SIFAT-SIFATNYA
Diajukan untuk memenuhi tugas mata kuliah Teori Himpunan Samar
Dosen : Prof. Dr. Agus Maman Abadi, M.,Si
Disusun oleh:
Arma Wangsa 20309251009
Nadya Amalia Juana 20309251021
PROGRAM MAGISTER PENDIDIKAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS NEGERI YOGYAKARTA
2021

2. OPERASI PADA HIMPUNAN SAMAR; ALPHA CUT DAN SIFAT-SIFATNYA
Operasi dasar pada himpunan klasik memuat komplemen, gabungan dan irisan.
Begitupun pada himpunan samar memuat operasi fuzzy standar seperti, komplemen,
gabungan dan irisan. Ketiganya merupakan operasi yang paling umum dalam aplikasi praktis
teori himpunan fuzzy.
A. Himpunan yang sama
Himpunan samar A dan B pada himpunan universal S dikatakan sama jika dan
hanya jika 𝜇𝐴(𝑥) = 𝜇𝐵(𝑥) untuk setiap 𝑥 anggota himpunan universal S.
B. Komplemen
Komplemen dilambangkan c pada himpunan tegas. Diberikan himpunan samar A
dituliskan 𝜇𝐴̅. Untuk setiap 𝑥 ∈ 𝑆, maka 𝜇𝐴(𝑥) merepresentasikan derajat keanggotaan x
pada himpunan samar A, sedangkan 𝜇𝐴̅(𝑥) merepresentasikan derajat keanggotaan yang
tidak termasuk ke dalam himpunan samar A. Fungsi keanggotaan komplemen pada
himpunan samar didefinisikan sebagai:
𝜇𝐴̅(𝑥) = 1 − 𝜇𝐴(𝑥)
Contoh:
1. Didefinisikan himpunan samar C adalah himpunan internet kecepatan tinggi pada
himpunan universal [0,100] dalam mbps dengan fungsi keanggotaan sebagai berikut:
𝜇𝐶 (𝑥) = {
0 𝑢𝑛𝑡𝑢𝑘 𝑥 ≤ 5
1 − 2 [
25 − 𝑥
20
]
2
𝑢𝑛𝑡𝑢𝑘 5 < 𝑥 ≤ 25
1 𝑢𝑛𝑡𝑢𝑘 𝑥 > 25
Grafik untuk fungsi keanggotaan himpunan C dapat dilihat pada gambar berikut.
Gambar 1. Contoh Komplemen

3. C. Gabungan
Gabungan himpunan samar A dan B merupakan himpunan samar pada himpunan
universal S yang dilambangkan dengan 𝜇𝐴 ∪ 𝜇𝐵 , dengan fungsi keanggotaan yang
didefinisikan sebagai berikut:
𝜇𝐴 ∪ 𝜇𝐵(𝑥) = 𝑚𝑎x [𝜇𝐴(𝑥),𝜇𝐵(𝑥)]
Contoh :
1. Diberikan himpunan universal S dari n pasien, yang disimbolkan dengan 1,2,…,n.
Diberikan A dan B himpunan samar yang menunjukkan pasien pada himpunan
universal S yang memiliki tekanan darah yang tinggi dan demam tinggi. Maka kita
dapat menentukan 𝜇𝐴 ∪ 𝜇𝐵 seperti pada ilustrasi Tabel 1 di bawah ini.
Tabel 1. Ilustrasi Standar Gabungan Fuzzy
Pasien A (tekanan darah) B (demam) 𝜇𝐴 ∪ 𝜇𝐵
1 1.0 1.0 1.0
2 0.5 0.6 0.6
3 1.0 0.1 1.0
… … … …
n 0.1 0.7 0.7
2. Misalkan terdapat gabungan antara himpunan samar mahasiswa berpengalaman dengan
komplemennya, dan himpunan siswa yang tidak memiliki pengalaman wisuda waktu
Sekolah Dasar SD. Perhatikan pada gambar di bawah ini pada area garis yang
ditebalkan.
Gambar 2. Contoh Gabungan dan komplemennya
𝐴 ∪ 𝐴̅ = 𝑋

4. Pada teori himpunan klasik tidak berlaku pada himpunan samar. Kita dapat dengan
mudah melihat bahwa aturan tersebut kontradiksi dengan himpunan samar. untuk
semua elemen x pada himpunan universal S bahwa 𝐴(𝑥) ∉ [0.1]
Misal : 𝐴(𝑥) = 0.6
Maka 𝐴̅(𝑥) = 1 − 0.6 = 0.4
𝐴 ∪ 𝐴̅(𝑥) = max[0.6,0.4] = 0.6
Maka x bukan merupakan bagian dari himpunan universal S karena telah melanggar
aturan.
D. Irisan
Irisan himpunan samar A dan B merupakan himpunan samar pada himpunan universal S
yang dilambangkan dengan 𝜇𝐴 ∩ 𝜇𝐵, yang dapat didefinisikan pada fungsi keanggotaan
sebagai berikut:
𝜇𝐴 ∩ 𝜇𝐵(𝑥) = 𝑚𝑖𝑛 [𝜇𝐴(𝑥), 𝜇𝐵(𝑥)]
Contoh:
Diberikan A yang menunjukkan himpunan fuzzy dari sungai-sungai terpanjang dan B yang
menunjukkan himpunan fuzzy sungai-sungai yang dapat dilalui untuk berlayar. Ilustrasi
pada Tabel 2 di bawah ini yang menunjukkan contoh dari 5 sungai-sungai tersebut.
Tabel 2. Ilustrasi Standar Irisan Fuzzy
Sungai
A (sungai
terpanjang)
B (sungai untuk
berlayar)
𝜇𝐴 ∩ 𝜇𝐵
Amazon 1.0 0.8 0.8
Nil 0.9 0.7 0.7
Yang-Tse 0.8 0.8 0.8
Danube 0.5 0.6 0.5
Rhein 0.4 0.3 0.3

5. E. Alpha Cut, Support, Core dan Hight
1. 𝜶-cut pada Himpunan Samar
Diberikan himpunan samar A dengan universal X, untuk semua 𝛼 ϵ [0,1], 𝛼-
cut dari suatu himpunan samar A adalah himpunan tegas yang memuat semua elemen
dari X dengan derajat keanggotaan dalam A yang lebih besar atau sama dengan 𝛼.
𝛼𝐴 = {x ϵ X | A(x) ≥ 𝛼}
Contoh:
Diberikan himpunan samar E yaitu himpunan buku yang mahal. Harga buku tersebut
berkisar dari harga 0 sampai 100 dolar. Derajat keanggotaan ditulis dalam bentuk
berikut.
X = {0,10, 20, ... 100}
E = {
0
0
+
0
10
+
0
20
+
0,2
30
+
0,4
40
+
0,6
50
+
0,8
60
+
1
70
+
1
80
+
1
90
+
1
100
}
Gambar 3. Grafik contoh himpunan E
Himpunan samar yang diberikan selalu dihubungkan dengan himpunan bagian
dari himpunan tegas dari X. Setiap himpunan bagian tersebut terdiri dari elemen-
elemen dari X yang derajat keanggotaannya di himpunan samar adalah termasuk ke
dalam himpunan bagian dari himpunan tegas yaitu [0,1]. Sebagai contoh, perhatikan
himpunan samar E, dari gambar di atas dapat kita lihat bahwa rentang harga buku yang
termasuk dalam himpunan dengan derajat keanggotaan pada interval tertutup [0.2,0.6]
digambarkan oleh interval tertutup [30,50], di mana itu adalah himpunan bagian dari

6. himpunan universal [0,100]. Sama halnya dengan rentang buku dari himpunan samar
dengan derajat keanggotaan kurang dari 0,8 yaitu [0,60]. Sedangkan untuk derajat
keanggotaan 0,8 atau lebih yaitu [0,0.6]. Pada umumnya, untuk setiap pembatasan
derajat keanggotaan, kita dapat menentukan himpunan bagian unik dari himpunan
universal [0,100].
0 E= [0,100] atau 0E = {0, 10,...., 100}
0,2E= [30,100] atau 0,2E = {30, 40,...., 100]
0,6E= [50,100] atau 0,6E = {50, 60,...., 100]
0,8E= [60,100] atau 0,8E = {60, 70,...., 100]
1E = [70,100] atau 1E = {70, 80,...., 100]
Dari contoh di atas dapat dilihat bahwa jika nilai 𝛼 bertambah maka ukuran 𝛼-
cut tidak bertambah, namun justru tetap atau berkurang. Sehingga untuk setiap
himpunan samar A, jika 𝛼1 < 𝛼2 maka 𝛼1𝐴
⊇ 𝛼2𝐴
dan berakibat:
𝛼1𝐴
∩ 𝛼2𝐴
= 𝛼2𝐴
𝛼1𝐴
∪ 𝛼2𝐴
= 𝛼1𝐴
2. Strong 𝜶-cut
Strong 𝛼-cut dari suatu himpunan samar A dilambangkan dengan 𝛼 +𝐴 dan
didefinisikan sebagai berikut:
𝛼 +𝐴 = {x ϵ X | A(x) > 𝛼}
Jadi strong 𝛼-cut merupakan himpunan tegas yang memuat semua anggota
pada himpunan universal dari himpunan samar A yang memiliki derajat keanggotaan
lebih dari nilai 𝛼 tertentu.
Contoh:
Menggunakan himpunan samar E pada contoh sebelumnya maka kita dapat
menentukan beberapa strong 𝛼-cut.
0+ E = (20,100]
0,2+E= (30,100]

7. 0,6+E= (50,100]
1+ E = ∅
Pada strong 𝛼-cut suatu himpunan samar juga berlaku sifat 𝛼-cut yaitu, untuk setiap
himpunan samar A, jika 𝛼1 < 𝛼2, maka 𝛼1+𝐴
⊇ 𝛼2+𝐴
dan berakibat :
𝛼1+𝐴
∩ 𝛼2+𝐴
= 𝛼+2𝐴
𝛼+1𝐴
∪ 𝛼2+𝐴
= 𝛼1+𝐴
Contoh 𝜶-cut dan strong 𝜶-cut
Dalam universal R diketahui himpunan samar B dengan fungsi keanggotaan sebagai
berikut:
B(x) = {
0 𝑢𝑛𝑡𝑢𝑘 𝑥 < 1
0,4 (𝑥 − 1) 𝑢𝑛𝑡𝑢𝑘 1 ≤ 𝑥 ≤ 3
0,8 𝑢𝑛𝑡𝑢𝑘 𝑥 > 3
Maka:
0,5B= {x ϵ R | 2.25 ≤ 𝑥 < ∞}
Dan
0,5+B= {x ϵ R | 2.25 < 𝑥 < ∞}
3. Support
Support dari himpunan samar A yang dilambangkan dengan Supp(A), adalah
himpunan tegas yang memuat semua unsur dari universal yang mempunyai derajat
keanggotaan lebih besar dari nol dalam himpunan samar A. Dapat juga di definisikan
sebagai strong α-cut untuk α = 0.
Supp(A) = 0+A = {x ϵ X | A(x) > 0}
Support himpunan samar E adalah (20,100]
4. Core
Core dari himpunan samar A, yang dilambangkan dengan core(A), adalah
himpunan tegas yang memuat semua unsur dari universal yang mempunyai derajat

8. keanggotaan sama dengan 1 (satu). Dapat juga di definisikan sebagai α-cut dengan α =
1.
Core(A) = 1A = {x ϵ X | A(x) ≥ 1} = {x ϵ X | A(x) = 1}
Core dari himpunan samar E adalah [70,100].
5. Hight
Height dari suatu himpunan samar A, yang dilambangkan dengan h(A). Dapat
juga didefinisikan sebagai nilai terbesar dari α-cut yang tidak kosong. Himpunan samar
yang tingginya sama dengan 1 disebut himpunan samar normal, sedangkan himpunan
samar yang tingginya kurang dari 1 disebut himpunan samar subnormal. Tinggi (height)
dari himpunan samar E adalah 1 (normal).
Untuk visualisasi dari α-cut, support, core, dan height dapat dilihat pada gambar
berikut:
Gambar 3. Visualisasi Dari Α-Cut, Support, Core, dan Height
6. Representasi 𝜶-cut
Salah satu cara untuk merepresentasikan himpunan samar adalah dengan
menggunakan 𝛼 − 𝑐𝑢𝑡.
Contoh:
Diketahui himpunan samar A pada himpunan universal 𝑆 = {𝑥1, 𝑥2,𝑥3, 𝑥4,𝑥5}, 𝐴 =
0.2
𝑥1
+
0.4
𝑥2
+
0.6
𝑥3
+
0.8
𝑥4
+
1
𝑥5
. Dapat direpresentasikan pada himpunan samar dengan menggunakan

9. 𝛼-cut, dengan cara menunjukkan apakah elemen tersebut masuk ke dalam 𝛼-cut yang
didefinisikan oleh nilai 𝛼. Himpunan A mengikuti nilai karakteristik fungsi seperti di
bawah ini:
0.2𝐴 =
1
𝑥1
+
1
𝑥2
+
1
𝑥3
+
1
𝑥4
+
1
𝑥5
0.4𝐴 =
0
𝑥1
+
1
𝑥2
+
1
𝑥3
+
1
𝑥4
+
1
𝑥5
0.6𝐴 =
0
𝑥1
+
0
𝑥2
+
1
𝑥3
+
1
𝑥4
+
1
𝑥5
0.8𝐴 =
0
𝑥1
+
0
𝑥2
+
0
𝑥3
+
1
𝑥4
+
1
𝑥5
1𝐴 =
0
𝑥1
+
0
𝑥2
+
0
𝑥3
+
0
𝑥4
+
1
𝑥5
Selanjutnya konversikan 𝛼 − 𝑐𝑢𝑡 menjadi himpunan samar 𝛼A khusus yang didefiniskan
untuk setiap x ∈ X sebagai berikut:
𝛼𝐴 = 𝛼 x 𝛼
𝐴
Sehingga dengan menggunakan rumus di atas didapat:
0.2𝐴 =
0.2
𝑥1
+
0.2
𝑥2
+
0.2
𝑥3
+
0.2
𝑥4
+
0.2
𝑥5
0.4𝐴 =
0
𝑥1
+
0.4
𝑥2
+
0.4
𝑥3
+
0.4
𝑥4
+
0.4
𝑥5
0.6𝐴 =
0
𝑥1
+
0
𝑥2
+
0.6
𝑥3
+
0.6
𝑥4
+
0.6
𝑥5
0.8𝐴 =
0
𝑥1
+
0
𝑥2
+
0
𝑥3
+
0.8
𝑥4
+
0.8
𝑥5
1𝐴 =
0
𝑥1
+
0
𝑥2
+
0
𝑥3
+
0
𝑥4
+
1
𝑥5
Gabungan khusus dari kelima himpunan samar di atas merupakan himpunan samar A itu
sendiri.
𝐴 ∪ 𝐵(𝑥) = 𝑚𝑎x [𝜇𝐴(𝑥), 𝜇𝐵(𝑥)]
(0.2A ∪ 0.4A ∪ 0.6A ∪ 0.8A ∪ 1A)(x) = max [0.2A(x), 0.4A(x), 0.6A(x), 0.8A(x), 1A(x)]
0.2A ∪ 0.4A ∪ 0.6A ∪ 0.8A ∪ 1A =
0.2
𝑥1
+
0.4
𝑥2
+
0.6
𝑥3
+
0.8
𝑥4
+
1
𝑥5
= A
Secara umum aturan tersebut disebutkan dalam Teorema 5.1 atau yang dikenal dengan

10. teorema dekomposisi fuzzy.
Teorema Dekomposisi Fuzzy
Diketahui A dan 𝐴
̃𝛼 himpunan samar di P dan 𝐴
̃𝛼 didefinisikan sebagai 𝜇𝐴
̃𝛼
(𝑥) =𝛼 𝐼𝐴
̃𝛼
,
maka:
𝐴 = ⋃ 𝐴
̃𝛼
𝛼∈[0,1]
Dimana ∪ merupakan gabungan dari himpunan samar standar (yaitu, sup dari 𝛼 ∈ [0,1]).
Bukti:
𝜇∪𝛼∈[0,1]
𝐴
̃𝛼 (𝑥) = 𝑠𝑢𝑝𝛼∈[0,1]𝜇𝐴
̃𝛼
(𝑥) = max[𝑠𝑢𝑝𝛼∈[0,𝛼] 𝜇𝐴
̃𝛼
(𝑥),𝑠𝑢𝑝𝛼∈[𝛼,1] 𝜇𝐴
̃𝛼
(𝑥)]
Untuk setiap 𝛼 ∈ [0,1] kita dapatkan 𝜇𝐴(𝑥) = 𝑎 < 𝑎 dan 𝑥 ∉ 𝐴
̃𝛼 hal tersebut berakibat
𝜇𝐴
̃𝛼
(𝑥) = 0. Jika 𝛼 ∈ [0,𝛼] , maka 𝜇𝐴(𝑥) = 𝑎 ≥ 𝑎 dan 𝑥 ∈ 𝐴
̃𝛼 dan kita dapatkan
𝜇𝐴
̃𝛼
(𝑥) = 𝛼. Oleh karena itu:
𝜇∪𝛼∈[0,1]
𝐴
̃𝛼(𝑥) = 𝑠𝑢𝑝𝛼∈[0,𝛼] 𝛼 = 𝛼 = 𝜇𝐴
̃𝛼
(𝑥)
Dari teorema di atas dapat disimpulkan bahwa jika 𝛼 − 𝑐𝑢𝑡 dapat ditentukan dari
himpunan samar untuk semua 𝛼 ∈ [0,1] kita dapat menunjukkan himpunan samar itu
sendiri. Oleh karena itu menentukan himpunan samar sama dengan menentukan semua
𝛼 − 𝑐𝑢𝑡 pada himpunan tersebut 𝛼 ∈ [0,1].
7. Cutworthy Properties Of Fuzzy Sets
Representasi dari 𝛼 − 𝑐𝑢𝑡 menunjukkan hal penting yang menghubungkan teori
himpunan klasik dan teori himpunan samar. Hubungan kedua teori ini dapat memperluas
berbagai sifat dari himpunan klasik menuju himpunan samar. Sifat dari himpunan klasik
dapat diperluas menjadi sifat himpunan samar melalui 𝛼 − 𝑐𝑢𝑡 dari himpunan samar yang
relevan. Beberapa sifat himpunan samar yang diturunkan dari himpunan klasik ini
dinamakan cutworthy properties.

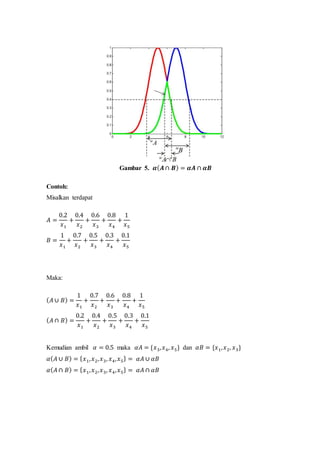
11. Contoh:
Definisi dari persamaan ini adalah
𝐴 = 𝐵 jika dan hanya jika 𝛼𝐴(𝑥) = 𝛼𝐵(𝑥)untuk semua 𝛼 ∈ [0,1]
Teorema 5.2
Untuk dua himpunan samar A, B dan 𝛼 ∈ [0,1]
a. 𝛼(𝐴 ∪ 𝐵) = 𝛼𝐴 ∪ 𝛼𝐵
b. 𝛼(𝐴 ∩ 𝐵) = 𝛼𝐴 ∩ 𝛼𝐵
Teorema tersebut dapat dipahami melalui ilustrasi di bawah ini:
a. 𝛼(𝐴 ∪ 𝐵) = 𝛼𝐴 ∪ 𝛼𝐵
Gambar 4. 𝜶(𝑨 ∪ 𝑩) = 𝜶𝑨 ∪ 𝜶𝑩
b. 𝛼(𝐴 ∩ 𝐵) = 𝛼𝐴 ∩ 𝛼𝐵

12. Gambar 5. 𝜶(𝑨 ∩ 𝑩) = 𝜶𝑨 ∩ 𝜶𝑩
Contoh:
Misalkan terdapat
𝐴 =
0.2
𝑥1
+
0.4
𝑥2
+
0.6
𝑥3
+
0.8
𝑥4
+
1
𝑥5
𝐵 =
1
𝑥1
+
0.7
𝑥2
+
0.5
𝑥3
+
0.3
𝑥4
+
0.1
𝑥5
Maka:
(𝐴 ∪ 𝐵) =
1
𝑥1
+
0.7
𝑥2
+
0.6
𝑥3
+
0.8
𝑥4
+
1
𝑥5
(𝐴 ∩ 𝐵) =
0.2
𝑥1
+
0.4
𝑥2
+
0.5
𝑥3
+
0.3
𝑥4
+
0.1
𝑥5
Kemudian ambil 𝛼 = 0.5 maka 𝛼𝐴 = {𝑥3,𝑥4, 𝑥5} dan 𝛼𝐵 = {𝑥1,𝑥2, 𝑥3}
𝛼(𝐴 ∪ 𝐵) = {𝑥1,𝑥2,𝑥3, 𝑥4,𝑥5} = 𝛼𝐴 ∪ 𝛼𝐵
𝛼(𝐴 ∩ 𝐵) = {𝑥1,𝑥2,𝑥3, 𝑥4,𝑥5} = 𝛼𝐴 ∩ 𝛼𝐵