2019/05/17

1. Introduction of NumPy for Python
NumPyのすゝめ 発表者：トビウオ

2. 初編
❖ 「天は(プログラミング)言語の上に言語を造らず言語の下に言語
を造らず」と言えり
❖ 広くこの言語世界を見渡すに、その(実行速度の)有様雲と泥の
相違あるに似たるはなんぞや
❖ 高速と低速との別はコンパイルとインタープリタとに
よりてできるものなり
元ネタ：福沢諭吉『学問のすゝめ』

3. 最適化はたいせつたいせつ
❖ コンパイルすると各種最適化が施されるが、インタープリタだ
とそれが行われない(JITなど例外あり)
インタープリタ言語コンパイラ言語
画像出典：いらすとや

4. そこにライブラリがあるじゃろ？
❖ スクリプト言語の書きやすさでコンパイラ言語
並の速度を出したい！
❖ 「主計算をライブラリに任せる」のが一つの解
❖ これから紹介するNumPyもライブラリの一つ

5. NumPyとは
❖ Python用の数値計算用ライブラリ
❖ 「配列(ベクトル・行列など)に数値(スカラー)や別の配
列を掛け合わせる」などの操作を高速化する
❖ 線形代数は今流行りの機械学習でもバンバン使われる
ので、非常に重要なライブラリ。ぜひ身につけよう
せんけいだいすう

6. NumPyの基本のキ
import numpy
# これはPythonにおける普通の配列
arr1 = [1, 2, 3, 4, 5]
# このメソッドで「NumPy用の配列(numpy.ndarray)」に変換する
np1 = numpy.array(arr1)
# 二次元以上の配列も作れる
arr2 = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 0]]
np2 = numpy.array(arr2)
# 四則演算もできる
print(np1 + 1) # [2 3 4 5 6]
print(np1 * 3) # [ 3 6 9 12 15]
print(np1 * np1) # [ 1 4 9 16 25]
print(np1 * np2) # [[ 1 4 9 16 25] [ 6 14 24 36 0]]
# ベクトル・行列としての計算もできる
np3 = numpy.array([1, 2, 3])
np4 = numpy.array([4, 5, 6])
print(numpy.dot(np3, np4)) # ベクトルの内積。値は32
print(numpy.cross(np3, np4)) # ベクトルの外積。値は[-3 6 -3]
np5 = numpy.array([[2, 4], [1, 3]])
np6 = numpy.array([[1.5, -2], [-.5, 1]])
print(np5 * np6) # 要素ごとの積。値は[[ 3. -8. ] [-0.5 3. ]]
print(numpy.dot(np5, np6)) # 行列積。値は[[1. 0.] [0. 1.]]
※他にも色々便利な
メソッドがあります

7. 「線形代数？なにそれおいしいの？」
❖ という人にもNumPyは効きます！
❖ 次以降のスライドで実例を示します

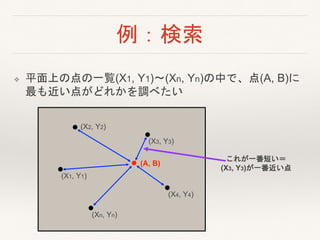
8. 例：検索
❖ 平面上の点の一覧(X1, Y1)〜(Xn, Yn)の中で、点(A, B)に
最も近い点がどれかを調べたい
(X1, Y1)
(X2, Y2)
(X3, Y3)
(X4, Y4)
(Xn, Yn)
(A, B)
これが一番短い＝
(X3, Y3)が一番近い点

9. 例：検索
❖ ただのPythonで書くとこんな感じ
❖ 検索される点が1000万個あると10.5秒掛かった
min_x, min_y, min_dist = math.nan, math.nan, math.inf # 最小距離な点の位置と距離
for index in range(0, point_len):
diff_x = point_x[index] - target_x
diff_y = point_y[index] - target_y
dist = math.sqrt(diff_x * diff_x + diff_y * diff_y) # 距離計算
if dist < min_dist:
min_x = point_x[index]
min_y = point_y[index]
min_dist = dist

10. 例：検索
❖ NumPyで書くとこんな感じ
❖ 検索される点が1000万個あると0.426秒掛かった
❖ 25倍近く高速に！
diff_x = point_x - target_x
diff_y = point_y - target_y
dist = numpy.sqrt(diff_x * diff_x + diff_y * diff_y)
min_index = dist.argmin()
min_x, min_y, min_dist = point_x[min_index], point_y[min_index], dist[min_index]

11. まとめ
❖ スクリプト言語をインタープリタ実行すると遅い
❖ ライブラリに計算を委ねることで高速化できる
❖ NumPyは応用が効くので是非マスターしよう