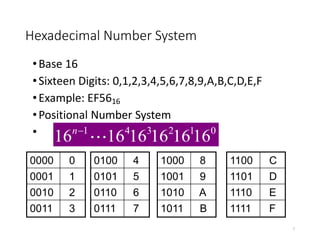
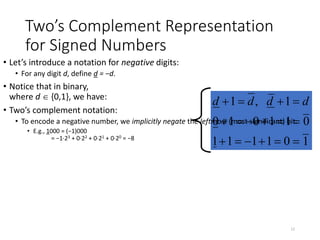
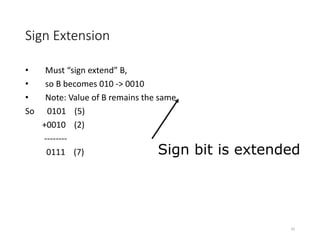
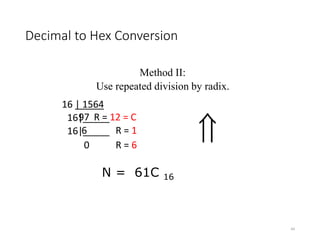
The document discusses different number systems including decimal, binary, octal, and hexadecimal. It explains the concept of a base-N number system and how digits are arranged from most to least significant. It then provides more details on the decimal, binary, octal, and hexadecimal number systems including examples. The document also covers topics like 1's complement, 2's complement, signed numbers, arithmetic operations, and number conversions between different bases.

1. Number Systems
Decimal, Binary, Octal and
Hexadecimal
1

2. Base-N Number System
•Base N
•N Digits: 0, 1, 2, 3, 4, 5, …, N-1
•Example: 1045N
•Positional Number System
•
2
• Digit do is the least significant digit (LSD).
• Digit dn-1 is the most significant digit (MSD).
1 4 3 2 1 0
1 4 3 2 1 0
n
n
N N N N N N
d d d d d d



3. DECIMAL NUMBER SYSTEM
•Base 10
•Ten Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
•Example: 104510
•Positional Number System
•Digit d0 is the least significant digit (LSD).
•Digit dn-1 is the most significant digit (MSD).
3
1 4 3 2 1 0
1 4 3 2 1 0
10 10 10 10 1010
n
n
d d d d d d



4. BINARY NUMBER SYSTEM
•Base 2
•Two Digits: 0, 1
•Example: 10101102
•Positional Number System
•Binary Digits are called Bits
•Bit bo is the least significant bit (LSB).
•Bit bn-1 is the most significant bit (MSB).
4
1 4 3 2 1 0
1 4 3 2 1 0
2 2 2 2 2 2
n
n
b b b b b b



5. OCTAL NUMBER SYSTEM
•Base 8
•Two Digits: 0, 1,2,3,4,5,6,7
•Example: 2178
•Positional Number System
•Bit bo is the least significant bit (LSB).
•Bit bn-1 is the most significant bit (MSB).
5

6. DECIMAL NUMBER SYSTEM
•Base 10
•Ten Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
•Example: 104510
•Positional Number System
•Digit d0 is the least significant digit (LSD).
•Digit dn-1 is the most significant digit (MSD).
6
1 4 3 2 1 0
1 4 3 2 1 0
10 10 10 10 1010
n
n
d d d d d d



7. Hexadecimal Number System
•Base 16
•Sixteen Digits: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
•Example: EF5616
•Positional Number System
•
7
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F
1 4 3 2 1 0
16 16 16 16 1616
n

8. 1’s Complements
• 1’s complement (or Ones’ Complement)
• To calculate the 1’s complement of a binary number just “flip” each bit of the
original binary number.
• E.g. 0  1 , 1  0
• 01010100100  10101011011
8

9. Why choose 2’s complement?
9

10. 2’s Complements
• 2’s complement
• To calculate the 2’s complement just calculate the 1’s complement, then add 1.
01010100100  10101011011 + 1=
10101011100
• Handy Trick: Leave all of the least significant 0’s and first 1 unchanged, and then
“flip” the bits for all other digits.
• Eg: 01010100100 -> 10101011100
10

11. Complements
• Note the 2’s complement of the 2’s complement is just the original
number N
• EX: let N = 01010100100
• (2’s comp of N) = M = 10101011100
• (2’s comp of M) = 01010100100 = N
11

12. Two’s Complement Representation
for Signed Numbers
1
0
1
1
1
1
0
1
1
0
1
0
1
,
1















 d
d
d
d
12
• Let’s introduce a notation for negative digits:
• For any digit d, define d = −d.
• Notice that in binary,
where d  {0,1}, we have:
• Two’s complement notation:
• To encode a negative number, we implicitly negate the leftmost (most significant) bit:
• E.g., 1000 = (−1)000
= −1·23 + 0·22 + 0·21 + 0·20 = −8

13. Negating in Two’s Complement
1
)
( 2
2 

 YZ
X
YZ
X
13
• Theorem: To negate
a two’s complement
number, just complement it and add 1.
• Proof (for the case of 3-bit numbers XYZ):
1
1
)
1
)(
1
(
1
11
100
)
1
(
)
(
2
2
2
2
2
2
2
2
2
















YZ
X
Z
Y
X
YZ
X
YZ
X
YZ
X
YZ
X
YZ
X
YZ
X

14. Signed Binary Numbers
• Two methods:
• First method: sign-magnitude
• Use one bit to represent the sign
• 0 = positive, 1 = negative
• Remaining bits are used to represent the magnitude
• Range - (2n-1 – 1) to 2n-1 - 1
where n=number of digits
• Example: Let n=4: Range is –7 to 7 or
• 1111 to 0111
14

15. Signed Binary Numbers
• Second method: Two’s-complement
• Use the 2’s complement of N to represent
-N
• Note: MSB is 0 if positive and 1 if negative
• Range - 2n-1 to 2n-1 -1
where n=number of digits
• Example: Let n=4: Range is –8 to 7
Or 1000 to 0111
15

16. Signed Numbers – 4-bit example
Decimal 2’s comp Sign-Mag
7 0111 0111
6 0110 0110
5 0101 0101
4 0100 0100
3 0011 0011
2 0010 0010
1 0001 0001
0 0000 0000
16
Pos 0

17. Signed Numbers-4 bit example
Decimal 2’s comp Sign-Mag
-8 1000 N/A
-7 1001 1111
-6 1010 1110
-5 1011 1101
-4 1100 1100
-3 1101 1011
-2 1110 1010
-1 1111 1001
-0 0000 (= +0) 1000
17

18. Signed Numbers-8 bit example
18

19. Notes:
•“Humans” normally use sign-magnitude
representation for signed numbers
• Eg: Positive numbers: +N or N
• Negative numbers: -N
•Computers generally use two’s-complement
representation for signed numbers
• First bit still indicates positive or negative.
• If the number is negative, take 2’s complement to
determine its magnitude
• Or, just add up the values of bits at their positions, remembering
that the first bit is implicitly negative.
19

20. Examples
•Let N=4: two’s-complement
•What is the decimal equivalent of
01012
Since MSB is 0, number is positive
01012 = 4+1 = +510
•What is the decimal equivalent of
11012 =
• Since MSB is one, number is negative
• Must calculate its 2’s complement
• 11012 = −(0010+1)= − 00112 or −310
20

21. Very Important!!! – Unless otherwise stated, assume two’s-
complement numbers for all problems, quizzes, HW’s, etc.
The first digit will not necessarily be
explicitly underlined.
21

22. Arithmetic Subtraction
• Borrow Method
• This is the technique you learned in grade school
• For binary numbers, we have
•
22
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 with a “borrow”
1

23. Binary Subtraction
• Note:
• A – (+B) = A + (-B)
• A – (-B) = A + (-(-B))= A + (+B)
• In other words, we can “subtract” B from A by “adding” –B to A.
• However, -B is just the 2’s complement of B, so to perform subtraction, we
• 1. Calculate the 2’s complement of B
• 2. Add A + (-B)
23

24. Binary Subtraction - Example
• Let n=4, A=01002 (410), and
B=00102 (210)
• Let’s find A+B, A-B and B-A
24
0 1 0 0
+ 0 0 1 0
 (4)10
 (2)10
0 11 0 6
A+B

25. Binary Subtraction - Example
25
0 1 0 0
- 0 0 1 0
 (4)10
 (2)10
10 0 1 0 2
A-B
0 1 0 0
+ 1 1 1 0
 (4)10
 (-2)10
A+ (-B)
“Throw this bit” away since n=4

26. Binary Subtraction - Example
26
0 0 1 0
- 0 1 0 0
 (2)10
 (4)10
1 1 1 0 -2
B-A
0 0 1 0
+ 1 1 0 0
 (2)10
 (-4)10
B + (-A)
1 1 1 02 = - 0 0 1 02 = -210

27. “16’s Complement” method
• The 16’s complement of a 16 bit Hexadecimal number is just:
=1000016 – N16
• Q: What is the decimal equivalent of B2CE16 ?
27

28. 16’s Complement
• Since sign bit is one, number is negative. Must calculate the 16’s
complement to find magnitude.
1000016 – B2CE16 = ?
• We have
10000
- B2CE
28

29. 16’s Complement
FFF10
- B2CE
29
2
3
D
4

30. 16’s Complement
• So,
1000016 – B2CE16 = 4D3216
= 4×4,096 + 13×256 + 3×16 + 2
= 19,76210
• Thus, B2CE16 (in signed-magnitude)
represents -19,76210.
30

31. Why does 2’s complement work?
31

32. Sign Extension
32

33. Sign Extension
• Assume a signed binary system
• Let A = 0101 (4 bits) and B = 010 (3 bits)
• What is A+B?
• To add these two values we need A and B to be of the same bit width.
• Do we truncate A to 3 bits or add an additional bit to B?
33

34. Sign Extension
• A = 0101 and B=010
• Can’t truncate A! Why?
• A: 0101 -> 101
• But 0101 <> 101 in a signed system
• 0101 = +5
• 101 = -3
34

35. Sign Extension
• Must “sign extend” B,
• so B becomes 010 -> 0010
• Note: Value of B remains the same
So 0101 (5)
+0010 (2)
--------
0111 (7)
35
Sign bit is extended

36. Sign Extension
• What about negative numbers?
• Let A=0101 and B=100
• Now B = 100  1100
36
Sign bit is extended
0101 (5)
+1100 (-4)
-------
10001 (1)
Throw away

37. Why does sign extension work?
•Note that:
(−1) = 1 = 11 = 111 = 1111 = 111…1
• Thus, any number of leading 1’s is equivalent, so long as the
leftmost one of them is implicitly negative.
•Proof:
111…1 = −(111…1) =
= −(100…0 − 11…1) = −(1)
•So, the combined value of any sequence of leading
ones is always just −1 times the position value of the
rightmost 1 in the sequence.
111…100…0 = (−1)·2n
37
n

38. Number Conversions
38

39. Decimal to Binary Conversion
39
Method I:
Use repeated subtraction.
Subtract largest power of 2, then next largest, etc.
Powers of 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2n
Exponent: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , n
210 2n
29
28
20 27
21 22 23 26
24 25

40. Decimal to Binary Conversion
40
Suppose x = 156410
Subtract 1024: 1564-1024 (210) = 540  n=10 or 1 in the (210)’s position
Thus:
156410 = (1 1 0 0 0 0 1 1 1 0 0)2
Subtract 512: 540-512 (29) = 28  n=9 or 1 in the (29)’s position
Subtract 16: 28-16 (24) = 12  n=4 or 1 in (24)’s position
Subtract 8: 12 – 8 (23) = 4  n=3 or 1 in (23)’s position
Subtract 4: 4 – 4 (22) = 0  n=2 or 1 in (22)’s position
28=256, 27=128, 26=64, 25=32 > 28, so we have 0 in all of these positions

41. Decimal to Binary Conversion
41
Method II:
Use repeated division by radix.
2 | 1564
782 R = 0
2|_____
391 R = 0
2|_____
195 R = 1
2|_____
97 R = 1
2|_____
48 R = 1
2|_____
24 R = 0
2|__24_
12 R = 0
2|_____
6 R = 0
2|_____
3 R = 0
2|_____
1 R = 1
2|_____
0 R = 1

Collect remainders in reverse order
1 1 0 0 0 0 1 1 1 0 0

42. Binary to Hex Conversion
42
1. Divide binary number into 4-bit groups
2. Substitute hex digit for each group
1 1 0 0 0 0 1 1 1 0 0
0
Pad with 0’s
If unsigned number
61C16
Pad with sign bit
if signed number

43. Hexadecimal to Binary Conversion
Example
43
1. Convert each hex digit to equivalent binary
(1 E 9 C)16
(0001 1110 1001 1100)2

44. Decimal to Hex Conversion
44
Method II:
Use repeated division by radix.
16 | 1564
97 R = 12 = C
16|_____
6 R = 1
16|_____
0 R = 6

N = 61C 16

45. Definitions
•nybble = 4 bits
•byte = 8 bits
•(short) word = 2 bytes = 16 bits
•(double) word = 4 bytes = 32 bits
•(long) word = 8 bytes = 64 bits
•1K (kilo or “kibi”) = 1,024
•1M (mega or “mebi”) = (1K)*(1K) = 1,048,576
•1G (giga or “gibi”) = (1K)*(1M) = 1,073,741,824
45