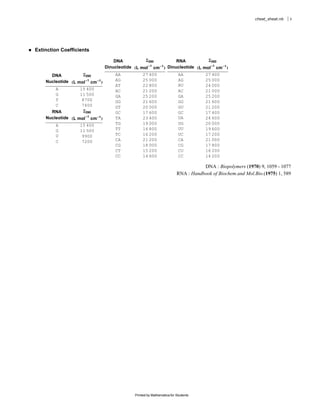
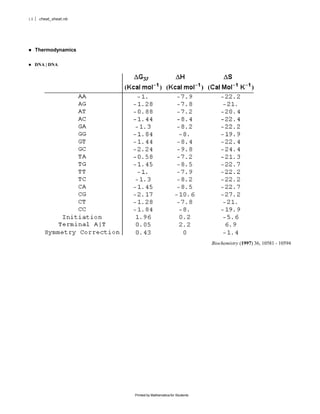
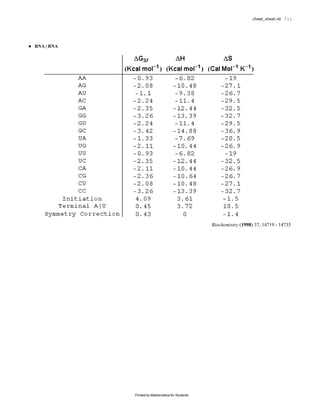
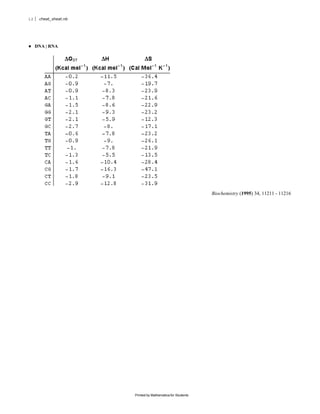
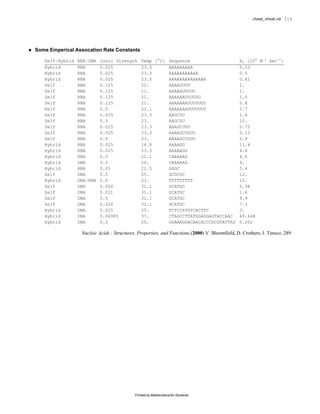
The document provides equations and definitions relating to mass, ionic strength, extinction coefficients, thermodynamics, kinetics, and empirical rate constants for nucleic acid hybridization and structure. Specifically, it defines equations for mass, ionic strength, linear and circular dichroism extinction coefficients, Gibbs free energy, equilibrium distributions for single and multiple equilibria, first and second order reaction kinetics, melting temperatures, and provides sample empirical association rate constants for RNA and DNA self-hybridization.

1. Equations
Mass
Mass Oligo Mass Base Terminal Correction
Ionic Strentgh
n
1
I ci z2
i
2 i 1
where
n is the number of different types of ions
ci is the concentration of each ion
zi is the number of charges on the ion
IUPAC definition
Extinction Coefficients
Linear
n n 1
260 Oligo 260 dinucleotidei 260 nucleotidei
i 1 i 2
Nucleic Acids: Structures, Properties, and Functions.(2000) V. Bloomfield, D. Crothers, I. Tinoco, 174-176
Circular
n
1
260 Oligo 260 dinucleotidei
2 i 1
Nucleic Acids: Structures, Properties, and Functions.(2000) V. Bloomfield, D. Crothers, I. Tinoco, 174-176
Hypochromicity correction
260 duplex 260 Top Strand 260 Bottom Strand 1 h260
where
h260 duplex 0.287 FractionAT duplex 0.059 FractionGC duplex
Biophys.Chem.(2008) 133, 66 - 70
Printed by Mathematica for Students

2. 2 cheat_sheat.nb
Thermodynamics
Gibbs Free Energy
GT H T S
GT R T Ln Keq
Individual Nearest Neighbor Hydrogen Bonding Model (INN - HB)
G Duplex
n 1
G dinucleotidei Initiation Correction Terminal Correction Symmetry Correction
i 1
where
Initiation Correction is applied to correct for initial complex formation
Terminal correction is applied once for each terminal A T or A U pair
Symmetry correction is applied if the sequence is self complimentary palindrome
Nucleic Acids: Structures, Properties, and Functions.(2000) V. Bloomfield, D. Crothers, I. Tinoco, 271-286
Equilibrium Distribution
Keq
A B
Equlibrium conditions :
B eq
Keq
A eq
Conservation of mass :
A eq B eq A 0 B 0
Substituting conservation of mass into equilibrium conditions yields :
B eq
Keq
A 0 B eq B 0
Solve for B eq :
A 0 B 0 Keq
B eq
1 Keq
A 0 B 0
A eq
1 Keq
Printed by Mathematica for Students

3. cheat_sheat.nb 3
KD
AB A+B
Equlibrium conditions :
A eq B eq
KD
AB eq
Conservation of mass :
Assuming all mass starts in AB 0
AB eq A eq AB 0
AB eq B eq AB 0
Substituting conservation of mass into equilibrium conditions yields the folowing polynomial:
2
AB 0 AB eq
KD
AB
Physically relevant solution to the polynomial:
1 1
A eq B eq KD KD 2 4 KD AB 0
2 2
1 1
AB eq AB 0 KD KD 2 4 KD AB 0
2 2
K Db K Dc
AB A+B AC A+C
Equlibrium conditions :
A eq B eq A eq C eq
KDb , KDc
AB eq AC eq
Conservation of mass :
Assuming all mass starts in AB 0 and C 0
AB eq AC eq A eq AB 0
AB eq B eq AB 0
AC eq C eq C 0
Substituting conservation of mass into equilibrium conditions and subsequent workup yields the folowing polynomial:
3 2
A eq Α A eq Β A eq Γ 0
where
Α KDb KDc A 0
Β KDb A 0 AB 0 KDb KDc
Γ KDb KDc AB 0
Physically relevant solution to the polynomial:
Printed by Mathematica for Students

4. 4 cheat_sheat.nb
Α 2 Θ
A eq Α2 3Β cos
3 3 3
Θ
AB 0 2 Α2 3Β cos 3
Α
B eq AB 0
Θ
3 KDb 2 Α2 3Β cos 3
Α
Θ
Α 2 Θ AB 0 2 Α2 3Β cos 3
Α
2
C eq C 0 AB 0 Α 3Β cos
3 3 3 Θ
3 KDb 2 Α2 3Β cos 3
Α
Θ
AB 0 2 Α2 3Β cos 3
Α
AB eq
Θ
3 KDb 2 Α2 3Β cos 3
Α
Θ
AB 0 2 Α2 3Β cos 3
Α Α 2 Θ
AC eq AB 0 Α2 3Β cos
Θ 3 3 3
3 KDb 2 Α2 3Β cos 3
Α
where
2 Α3 9 ΑΒ 27 Γ
Θ arccos
3
2 Α2 3Β
FEBS letters 1995, 360, 111-4
Melting Temperatures
A+A AA
H
Tn
S R Ln Ct
Where
Ct 2 A 0
Nucleic Acids: Structures, Properties, and Functions.(2000) V. Bloomfield, D. Crothers, I. Tinoco, 273
A+B AB
H
Tn
Ct
S R Ln 4
Where
Ct 2 A 0
Nucleic Acids: Structures, Properties, and Functions.(2000) V. Bloomfield, D. Crothers, I. Tinoco, 273
Printed by Mathematica for Students

5. cheat_sheat.nb 5
Nucleic Acids: Structures, Properties, and Functions.(2000) V. Bloomfield, D. Crothers, I. Tinoco, 273
Elementary Reaction Kinetics
Detailed Balance
For a reversible first order equilibrium is defined as the point at which the forward reaction rate is equal to the
reverse reaction rate, and therefore:
kf A eq kb B eq
kb B eq
kf
A eq
kf B eq
kb A eq
Furthermore thermodynamics tells us that for a reversible first order equilibrium is defined as:
B eq
Keq
A eq
kf
Keq
kb
This works regardless of the order of reaction. For example, in the case of a second order reaction A + B C
kf A eq B eq
kb C eq
kb C eq
kf
A eq B eq
kf C eq
kb A eq B eq
And thermodynamics tells us for a second order reaction:
C eq
Keq
A eq B eq
kf
Keq
kb
And thus regardless of the order of the reaction:
kf
Keq
kb
Physical Chemistry Kinetics, (2006) Horia Metiu, 78
First-Order Irreversible
Printed by Mathematica for Students

6. 6 cheat_sheat.nb
First-Order Irreversible
k
A B
kt
Η t A 0 1 A 0
where
A t A 0 Η t
B t B 0 Η t
Physical Chemistry Kinetics, (2006) Horia Metiu, 27
First-Order Reversible
kf
A B
kb
kb B 0 kf A 0 kb kf t
Η t 1
kb kf
where
A t A 0 Η t
B t B 0 Η t
Physical Chemistry Kinetics, (2006) Horia Metiu, 73
A 0 kf B 0 kb
Ηeq
kb kf
where
A eq A 0 Ηeq
B eq B 0 Ηeq
Physical Chemistry Kinetics, (2006) Horia Metiu, 78
Second-Order Irreversible
k
A B C
A B A 0 kt B 0 kt
0 0
Η t
A A 0 kt B B 0 kt
0 0
where
A t A 0 Η t
B t B 0 Η t
C t C 0 Η t
Physical Chemistry Kinetics (2006) Horia Metiu, 54
Printed by Mathematica for Students

7. cheat_sheat.nb 7
k
2A B
A 2 kt
0
Η t
2 1 A 0 kt
where
A t A 0 Η t
B t B 0 2Η t
Physical Chemistry Kinetics, (2006) Horia Metiu, 57
Second-Order Reversible
General Solution :
2 e0
Η t
t
e1 Coth 2
where
e1 2 4 e0 e2
Physical Chemistry Kinetics, (2006) Horia Metiu, 99
kf
A B C
kb
e0 kf A 0 kb B 0 C 0
e1 kf kb B 0 C 0
e2 kb
where
A t A 0 Η t
B t B 0 Η t
C t C 0 Η t
Physical Chemistry Kinetics, (2006) Horia Metiu, 93
kf
A B C
kb
e0 kf A 0 B 0 kb C 0
e1 kf A 0 B 0 kb
e2 kf
where
A t A 0 Η t
B t B 0 Η t
C t C 0 Η t
Physical Chemistry Kinetics, (2006) Horia Metiu, 93
Printed by Mathematica for Students

8. 8 cheat_sheat.nb
Physical Chemistry Kinetics, (2006) Horia Metiu, 93
kf
A B C D
kb
e0 kf A 0 B 0 kb C 0 D 0
e1 kf A 0 B 0 kb C 0 D 0
e2 kf kb
where
A t A 0 Η t
B t B 0 Η t
C t C 0 Η t
D t D 0 Η t
Physical Chemistry Kinetics, (2006) Horia Metiu, 94
Constants
Mass
Printed by Mathematica for Students

9. cheat_sheat.nb 9
Extinction Coefficients
DNA 260 RNA 260
1 1 1 1
Dinucleotide L mol cm Dinucleotide L mol cm
DNA 260 AA 27 400 AA 27 400
Nucleotide 1 1 AG 25 000 AG 25 000
L mol cm
AT 22 800 AU 24 000
A 15 400 AC 21 200 AC 21 000
G 11 500 GA 25 200 GA 25 200
T 8700 GG 21 600 GG 21 600
C 7400 GT 20 000 GU 21 200
RNA 260 GC 17 600 GC 17 400
1 1
Nucleotide L mol cm TA 23 400 UA 24 600
A 15 400 TG 19 000 UG 20 000
G 11 500 TT 16 800 UU 19 600
U 9900 TC 16 200 UC 17 200
C 7200 CA 21 200 CA 21 000
CG 18 000 CG 17 800
CT 15 200 CU 16 200
CC 14 600 CC 14 200
DNA : Biopolymers (1970) 9, 1059 - 1077
RNA : Handbook of Biochem.and Mol.Bio.(1975) 1, 589
Printed by Mathematica for Students

10. 10 cheat_sheat.nb
Thermodynamics
DNA | DNA
Biochemistry (1997) 36, 10581 - 10594
Printed by Mathematica for Students

11. cheat_sheat.nb 11
RNA | RNA
Biochemistry (1998) 37, 14719 - 14735
Printed by Mathematica for Students

12. 12 cheat_sheat.nb
DNA | RNA
Biochemistry (1995) 34, 11211 - 11216
Printed by Mathematica for Students

13. cheat_sheat.nb 13
Some Emperical Assocation Rate Constants
Self Hybrid RNA DNA Ionic Strength Temp °C Sequence kf 106 M 1 Sec 1
Hybrid RNA 0.025 23.3 AAAAAAAAA 0.53
Hybrid RNA 0.025 23.3 AAAAAAAAAAA 0.5
Hybrid RNA 0.025 23.5 AAAAAAAAAAAAAA 0.61
Self RNA 0.125 21. AAAAUUUU 1.
Self RNA 0.125 21. AAAAAUUUUU 2.
Self RNA 0.125 21. AAAAAAUUUUUU 1.5
Self RNA 0.125 21. AAAAAAAUUUUUUU 0.8
Self RNA 0.5 22.1 AAAAAAAUUUUUUU 2.7
Self RNA 0.025 23.3 AAGCUU 1.6
Self RNA 0.5 23. AAGCUU 10.
Self RNA 0.025 23.3 AAAGCUUU 0.75
Self RNA 0.025 23.3 AAAAGCUUUU 0.13
Self RNA 0.5 23. AAAAGCUUUU 0.9
Hybrid RNA 0.025 16.8 AAAAGG 11.4
Hybrid RNA 0.025 23.3 AAAAAGG 4.4
Hybrid RNA 0.5 21.1 CAAAAAG 4.6
Hybrid DNA 0.5 20. CAAAAAG 9.
Hybrid RNA 0.05 21.5 GGGC 5.4
Self DNA 0.5 25. GCGCGC 12.
Hybrid DNA RNA 0.5 23. TTTTTTTTT 10.
Self DNA 0.006 31.1 GCATGC 0.98
Self DNA 0.021 31.1 GCATGC 1.6
Self DNA 0.5 31.1 GCATGC 9.9
Self DNA 0.026 31.1 GCATGC 7.3
Hybrid DNA 0.025 25. TCTCCATGTCACTTC 3.
Hybrid DNA 0.06985 37. CTAGCCTTATGGAGGAGTACCAAC 69.448
Hybrid DNA 0.5 25. GGAAAGGACAACACCCGCGTATTAG 0.202
Nucleic Acids : Structures, Properties, and Functions.(2000) V. Bloomfield, D. Crothers, I. Tinoco, 289
Printed by Mathematica for Students