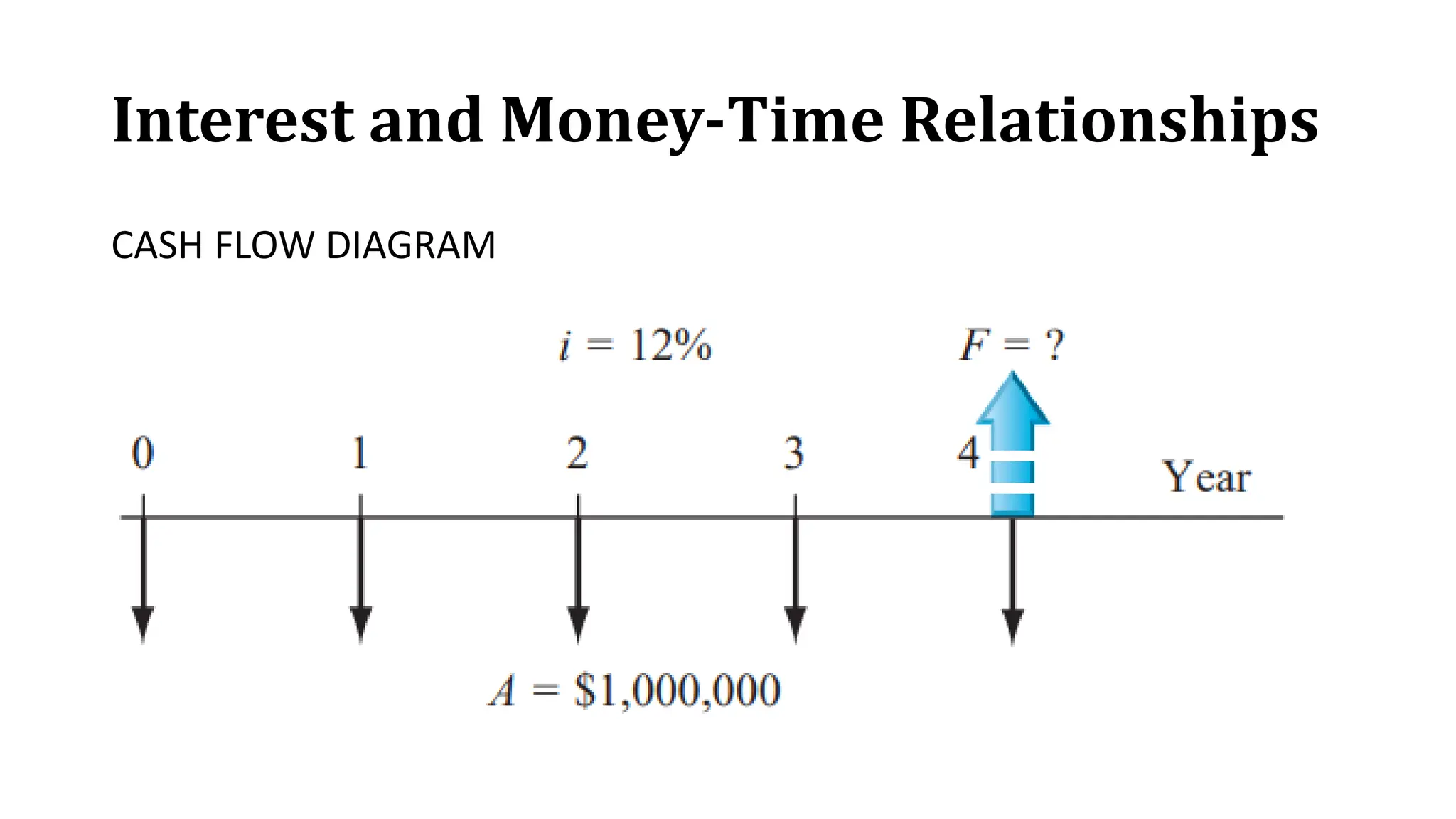
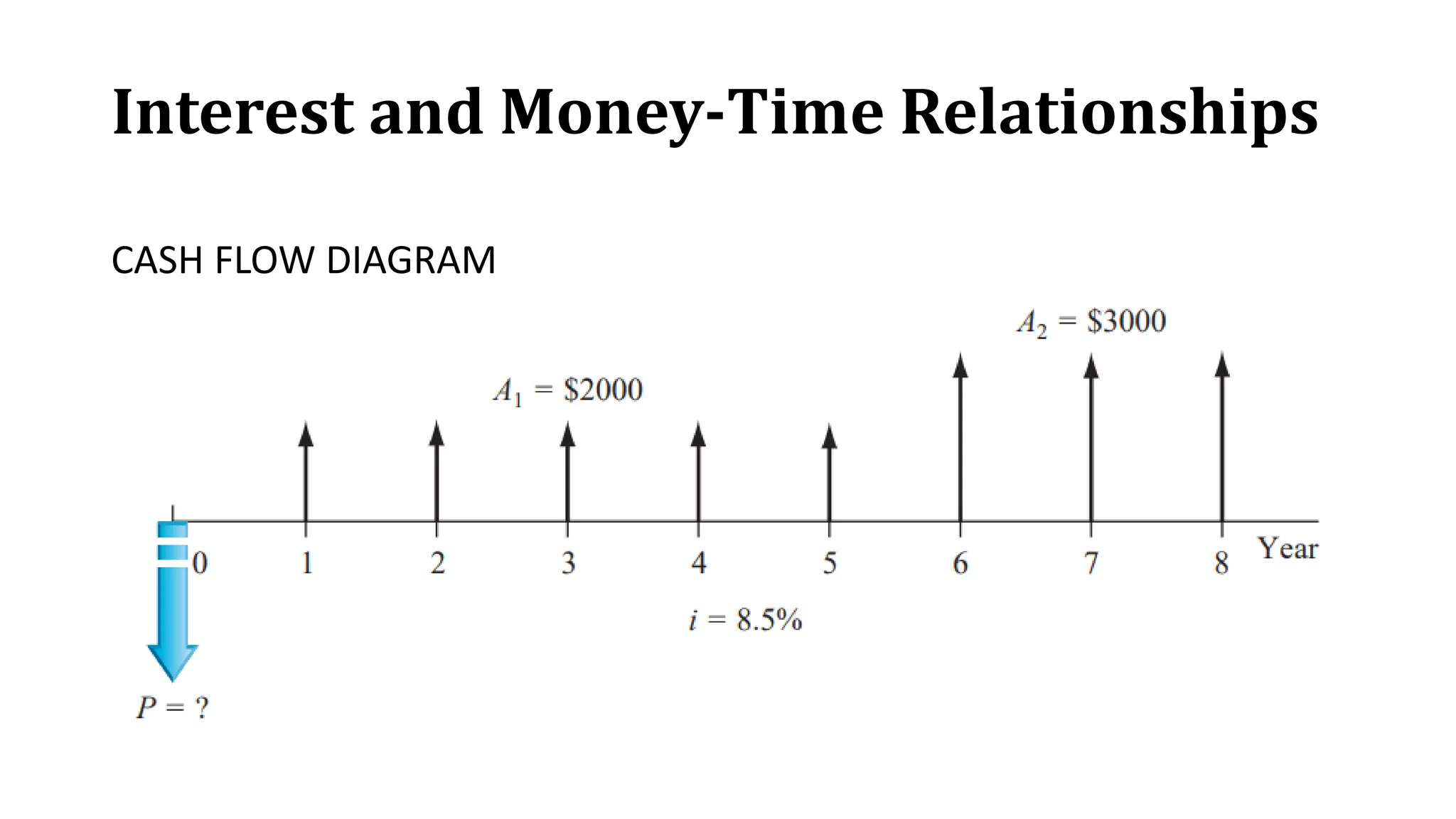
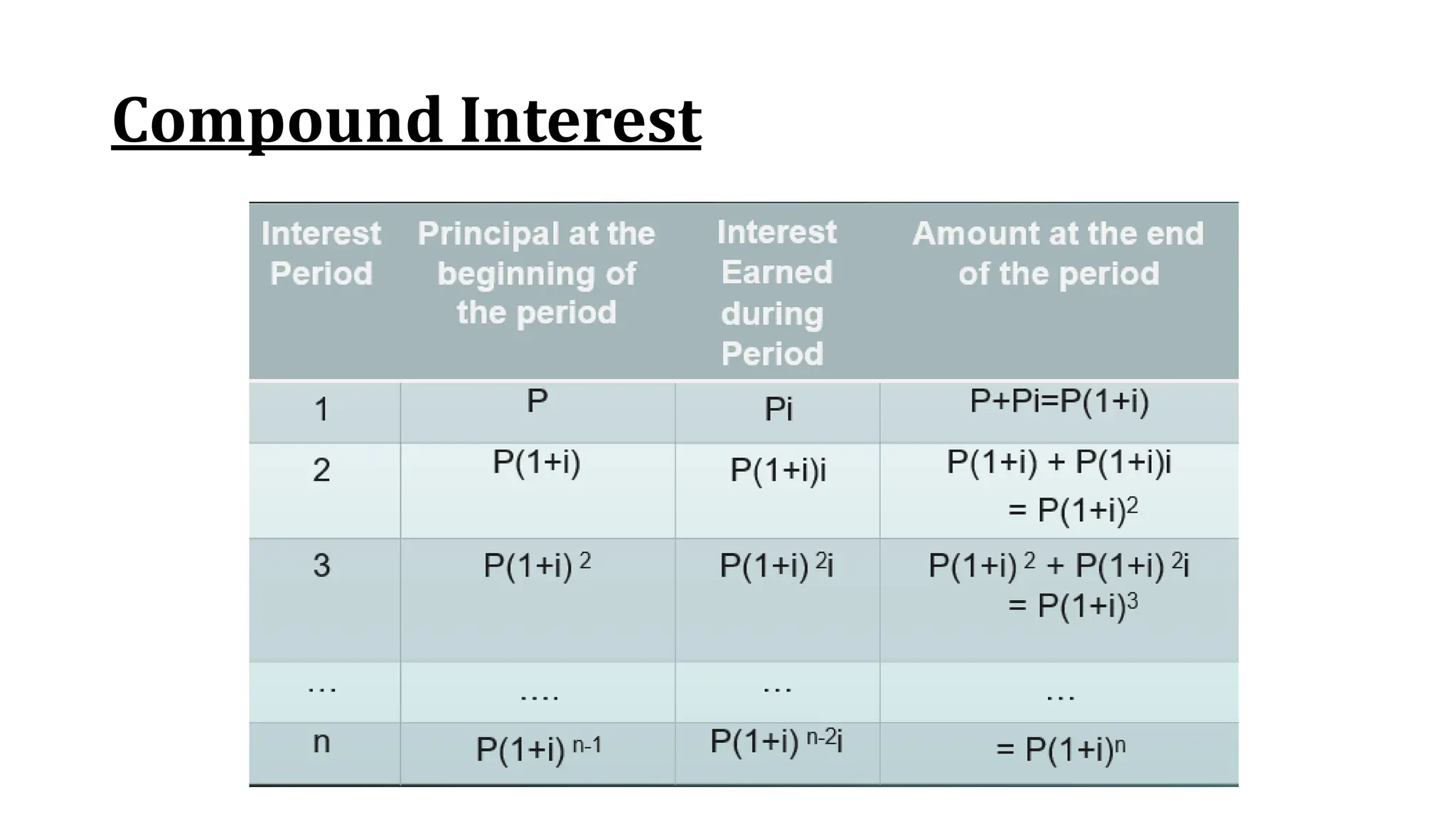
The document outlines key learning outcomes related to cash flow and interest rates, including calculations for compound interest and the use of cash flow diagrams. It provides examples for different scenarios involving loans, investments, and effective vs. nominal interest rates, demonstrating how to calculate future worth and present value. Additionally, the document addresses continuous compounding and compares different compounding frequencies.

1. Cashflow and Interest
Rate

2. Learning Outcomes
1. Perform calculations for compound interest
2. Graphically represent cash flow
3. Understand and use nominal and effective interest rates in
engineering or daily practices.

3. Interest and Money-Time Relationships
Cash-Flow Diagrams
Cash-Flow Diagram – is a graphical representation of cash flows drawn
on a time scale.
↑ - receipt (positive cash flow or cash inflow)
↓ - disbursement (negative cash flow or cash outflow)

4. Interest and Money-Time Relationships
Cash-Flow Diagrams
Example: A loan of P100 at simple interest will become P150 after 5
years.
Cash flow diagram on the
viewpoint of the lender.
Cash flow diagram on the
viewpoint of the borrower.

5. Interest and Money-Time Relationships
Example:
Each year Exxon-Mobil expends large amounts of funds for
mechanical safety features throughout its worldwide operations.
Carla Ramos, a lead engineer for Mexico and Central American
operations, plans expenditures of $1 million now and each of the next
4 years just for the improvement of field-based pressure-release
valves. Construct the cash flow diagram to find the equivalent value
of these expenditures at the end of year 4, using a cost of capital
estimate for safety-related funds of 12% per year.

6. Interest and Money-Time Relationships
CASH FLOW DIAGRAM

7. Interest and Money-Time Relationships
Example:
An electrical engineer wants to deposit an amount P now such that she
can withdraw an equal annual amount of A1= $2000 per year for the
first 5 years, starting 1 year after the deposit, and a different annual
withdrawal of A2 =$3000 per year for the following 3 years. How would
the cash flow diagram appear if i= 8.5% per year?

8. Interest and Money-Time Relationships
CASH FLOW DIAGRAM

9. Compound Interest
For compound interest, the interest accrued for each interest period is
calculated on the principal plus the total amount of interest
accumulated in all previous periods. Thus, compound interest means
interest on top of interest.
Compound interest = (principal + all accrued interest)(interest rate)

10. Compound Interest

11. Cash flow of Compound Interest on
Borrower’s Point of View
Cash flow Future Worth, F:
F = P(1+i)n
Where:
i = effective interest per interest
period
i =
nominal interest rate (𝑟)
number of compounding per year (m)
n = total number of compounding

12. Compound Interest
To compute values of i and n:
nominal interest rate = 12%
number of years of investment = 6 years
a. compounded annually d. compounded monthly
i= 0.12/1 = 0.12 i= 0.12/12 = 0.01
n = 6(1) = 6 n = 6(12) = 72
b. compounded semi-annually e. compounded bi-monthly
i= 0.12/2 = 0.06 i= 0.12/6 = 0.02
n = 6(2) = 12 n = 6(6) = 36
c. compounded quarterly
i= 0.12/4 = 0.03
n = 6(4) = 24

13. Cash flow of Compound Interest on
Borrower’s Point of View
Single Payment Compound Amount Factor, F/P:
F= 𝑷 𝟏 + 𝒊 𝒏
The quantity (1+i)n is commonly called “single payment compound amount
factor” designated by the functional symbol (F/P, i%, n) thus
F = P(F/P,i%, n)
The symbol F/P, i% , n is read as “F given P at i percent in n interest period”

14. Cash flow of Compound Interest on
Borrower’s Point of View
Single Payment Present Worth Factor, P/F:
P= 𝑭 𝟏 + 𝒊 −𝒏
The quantity (1+i)-n is commonly called “single payment present worth
factor” designated by the functional symbol P/F, i%,n thus
P = F(P/F, i%, n)
The symbol P/F, i% , n is read as “P given F at i percent in n interest
period”

15. Rates of Interest
• A nominal interest rate (r) is an interest rate that does not account
for compounding.
i =
𝒓
𝒎
• An effective interest rate (i) is a rate wherein the compounding of
interest is taken into account. Effective rates are commonly
expressed on an annual basis as an effective annual rate; however,
any time basis may be used.

16. Compound Interest
Effective Rate of Interest, ER:
ER =
interest earned in one year
principal during that year
=
F − P
P
= (1+i )n - 1
Equivalent Rates:
ER1 = ER2

17. Example of Effective Annual Interest
Rate
Consider these two offers: Investment A pays 10%
interest, compounded monthly. Investment B pays
10.1%, compounded semiannually. Which is the
better offer?

18. Sample Problem
Assume an engineering company borrows $100,000 at 10% per year
compound interest and will pay the principal and all the interest after 3
years. Compute the annual interest and total amount due after 3 years.
Given:
P = $100,000
r = 10% = 0.10
m = 1
n = 3(1)

19. Solution
Long Method
To include compounding of interest, the annual interest and total
owed each year are calculated.
Interest, year 1: 100,000(0.10) = $10,000
Total due, year 1: 100,000 + 10,000 = $110,000
Interest, year 2: 110,000(0.10) = $11,000
Total due, year 2: 110,000 + 11,000 = $121,000
Interest, year 3: 121,000(0.10) $12,100
Total due, year 3: 121,000 + 12,100 = $133,100

20. Short Method
Using the formula F = P(1+i)n
F= 100,000(1+0.10)3
F = 133,100

21. Interest and Money-Time Relationships
Compound Interest
Example 1:
The amount of P 20,000 was deposited in a bank earning an
interest rate of 6.5% per annum. Determine the total amount
at the end of 7 years if the principal and interest were not
withdrawn during this period.
Ans. P 31,079.73

22. Interest and Money-Time Relationships
Compound Interest
Example 2:
A man expects to receive P 25,000 in 8 years. How much is
that money worth now considering interest at 8%
compounded quarterly?
Ans. P13,265.83

23. Interest and Money-Time Relationships
Compound Interest
Example 3:
How many years will P 100,000 earn a compounded interest
of P 50,000 if interest is 9% compounded quarterly?
Ans. 4.56 years

24. Interest and Money-Time Relationships
Compound Interest
Example 4:
A sum of P 1,000.00 is invested now and left for eight years, at
which time the principal is withdrawn. The interest has
accrued is left for another eight years. If the effective annual
interest rate is 5%, what will be the withdrawal amount at the
end of the 16th year?
Ans. P 705.42

25. Interest and Money-Time Relationships
Compound Interest
Example 5:
If money is worth 5% compounded quarterly, find the equated
time for paying a loan of P 150,000 due in one year and P
280,000 in 2 years.
Ans. 1.6455 years

26. Interest and Money-Time Relationships
Compound Interest
Example 6:
How long will it take money to double itself if invested at 5%
compounded annually?

27. Interest and Money-Time Relationships
Compound Interest
Example 7:
Compute the equivalent rate of 6% compounded semi-
annually to a rate compounded quarterly.

28. Interest and Money-Time Relationships
Compound Interest
Example 8:
If P5, 000.00 shall accumulate for 10 years at 8%
compounded quarterly. Find the compounded interest at the
end of 10 years.

29. Continuous Compounding
𝐹 = 𝑃(𝑒)𝑁𝑅(𝑁)
• Where:
P = Principal
e = 2.71828…..
NR = nominal rate
n = number of years
e(NR)n = continuous compounding amount factor

30. Continuous Compounding
Sample:
Compare the accumulated amounts after 5 years of P5,000 at an
interest rate of 10% compounded (a) annually (b) semi annually (c)
quarterly (d) monthly (e) daily (f) continuously