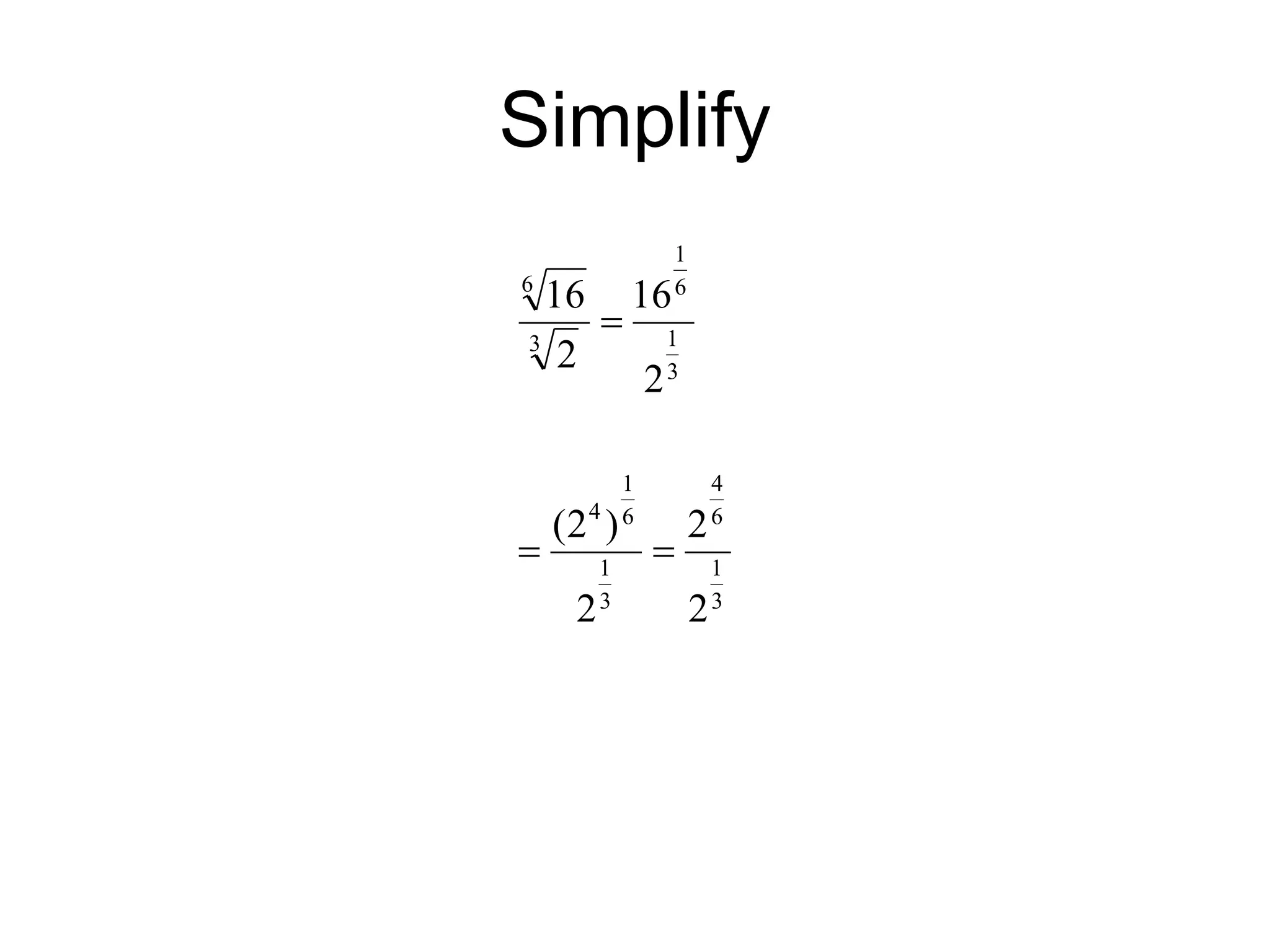
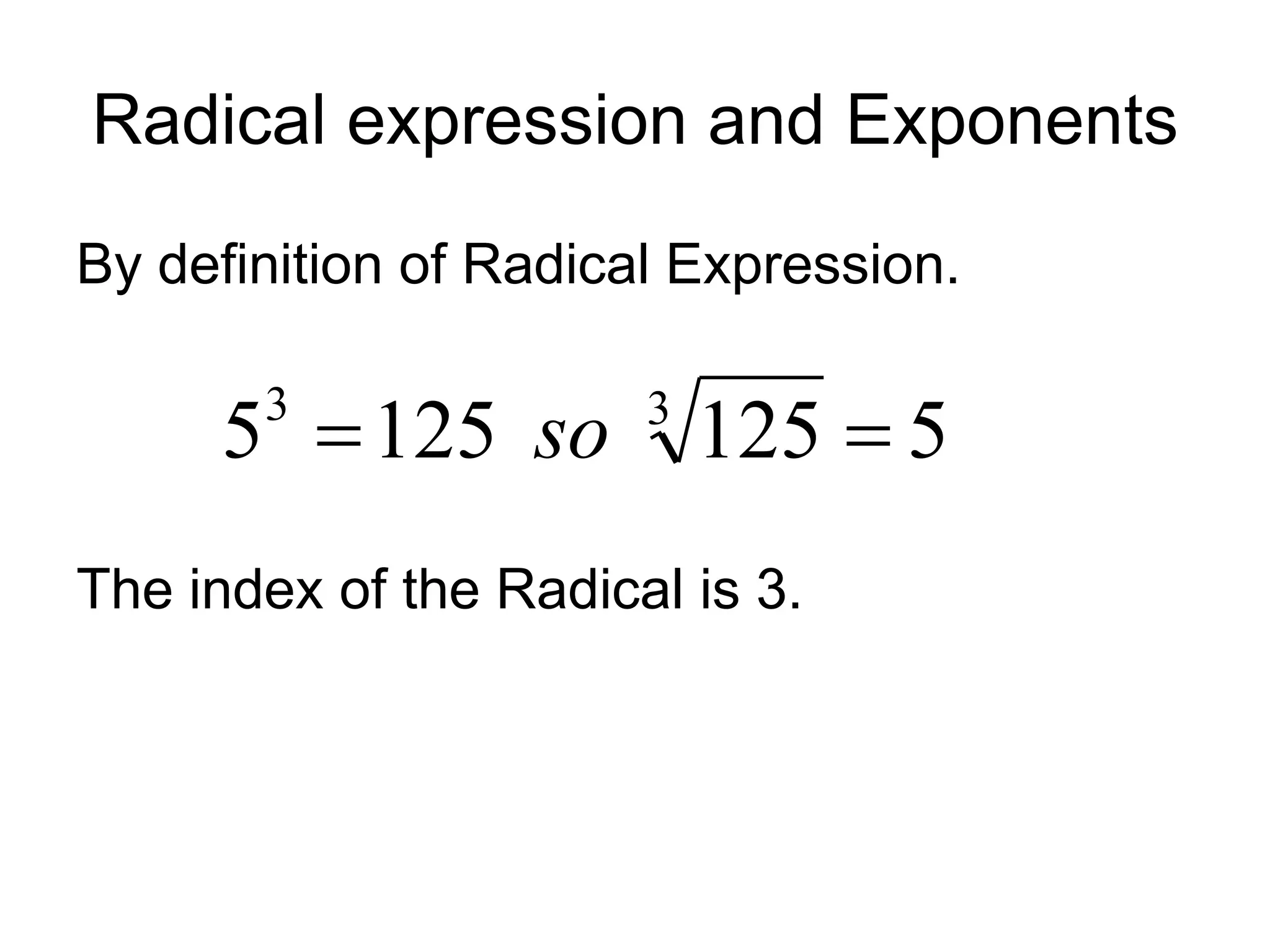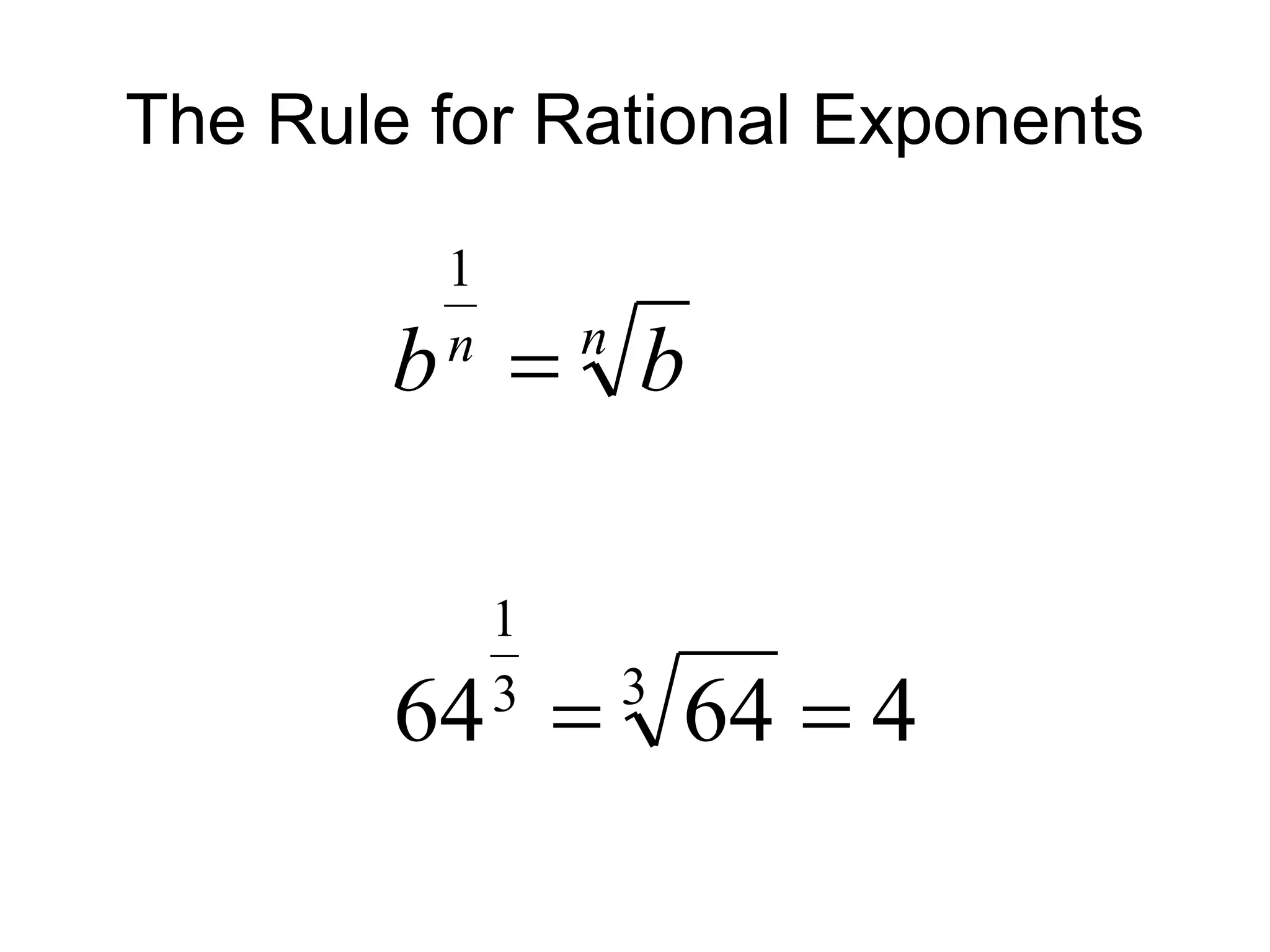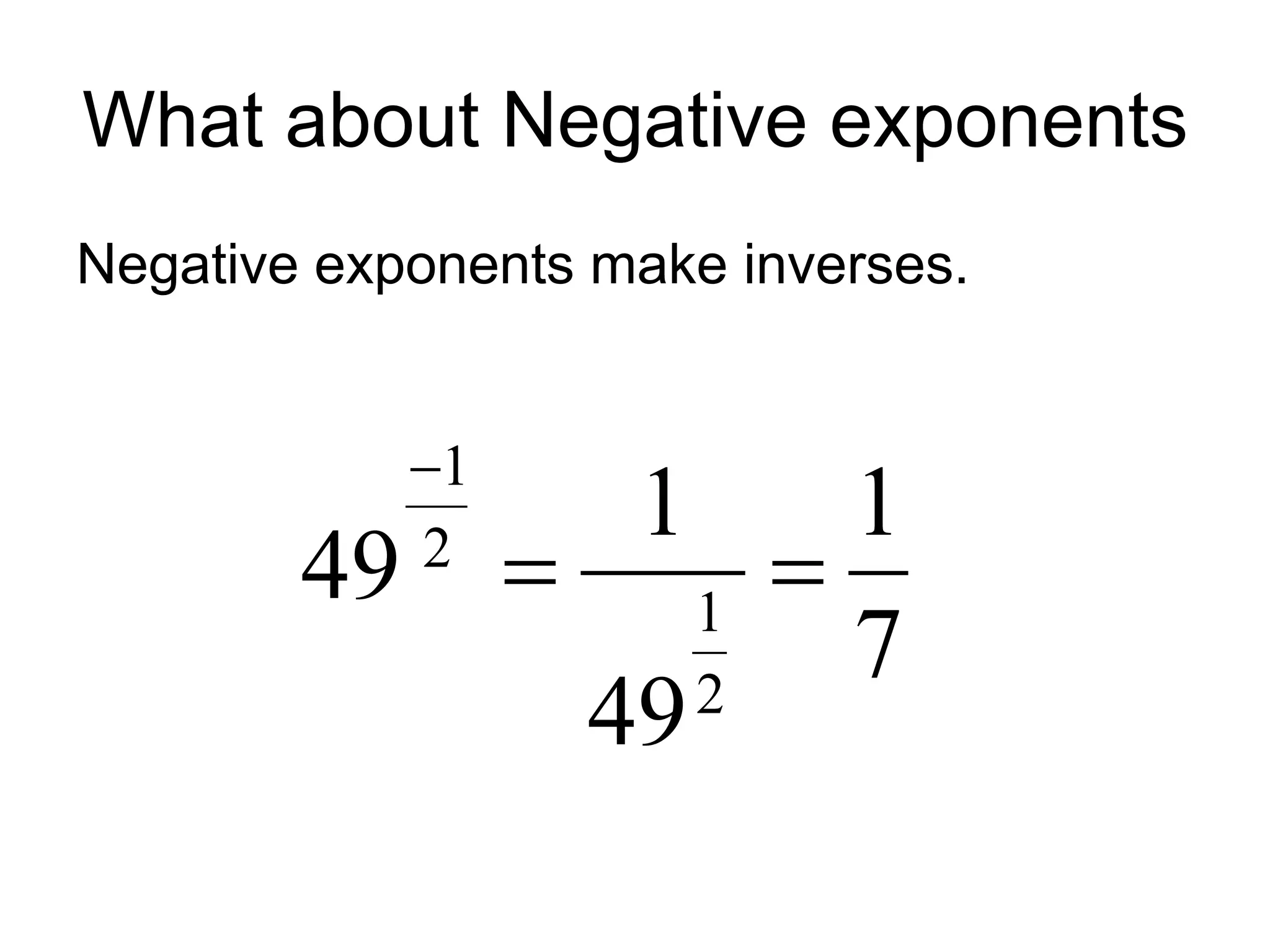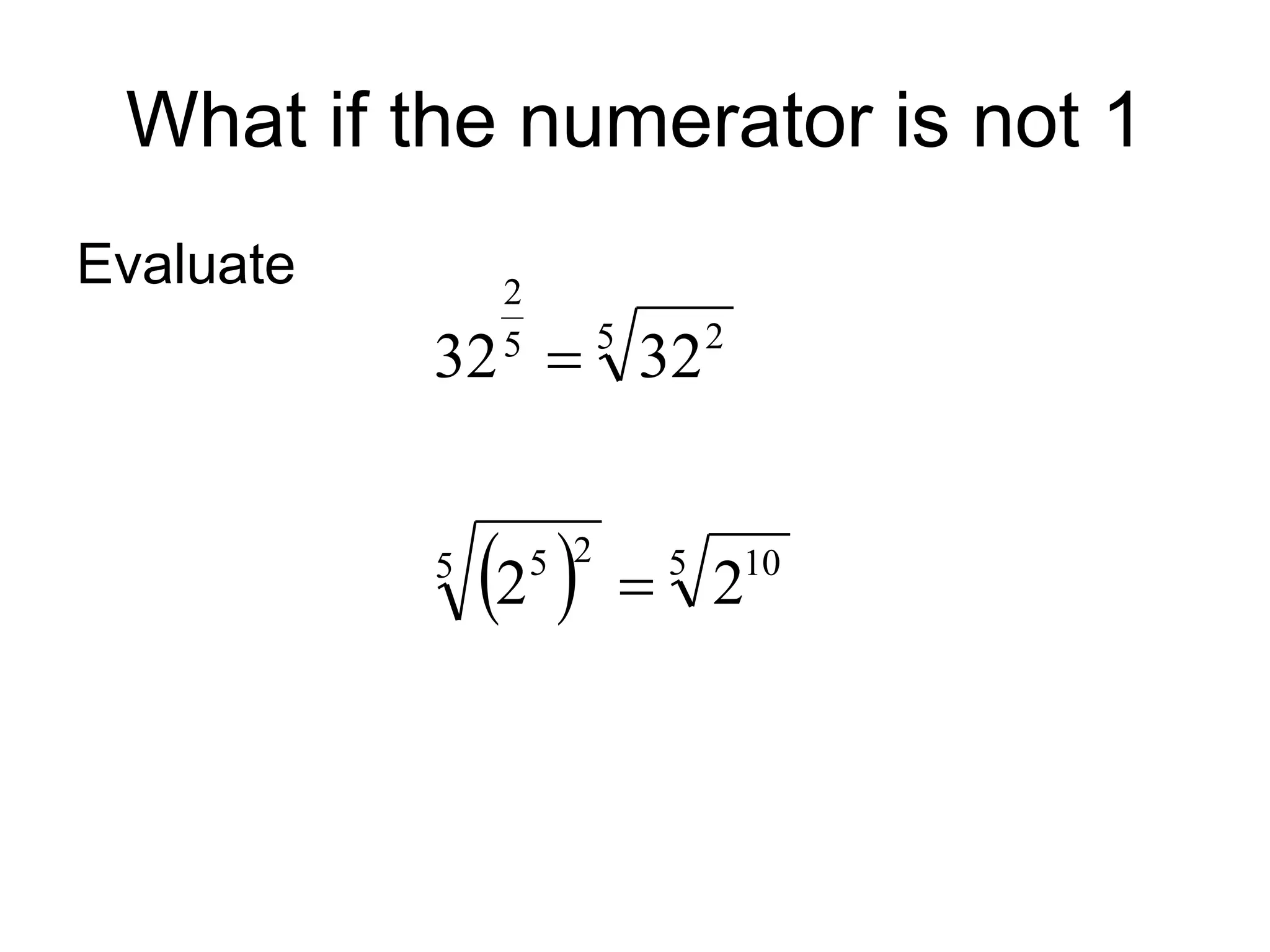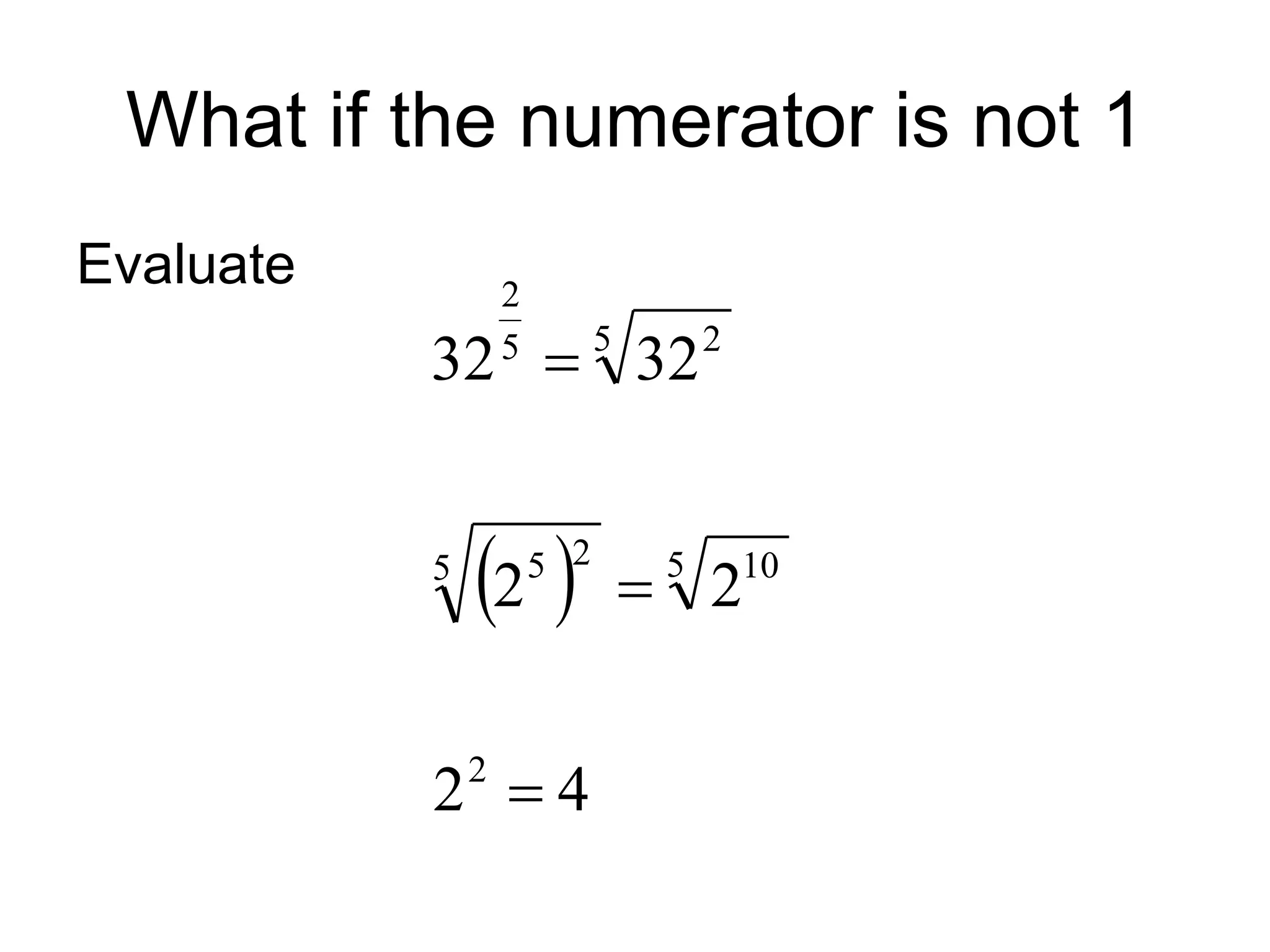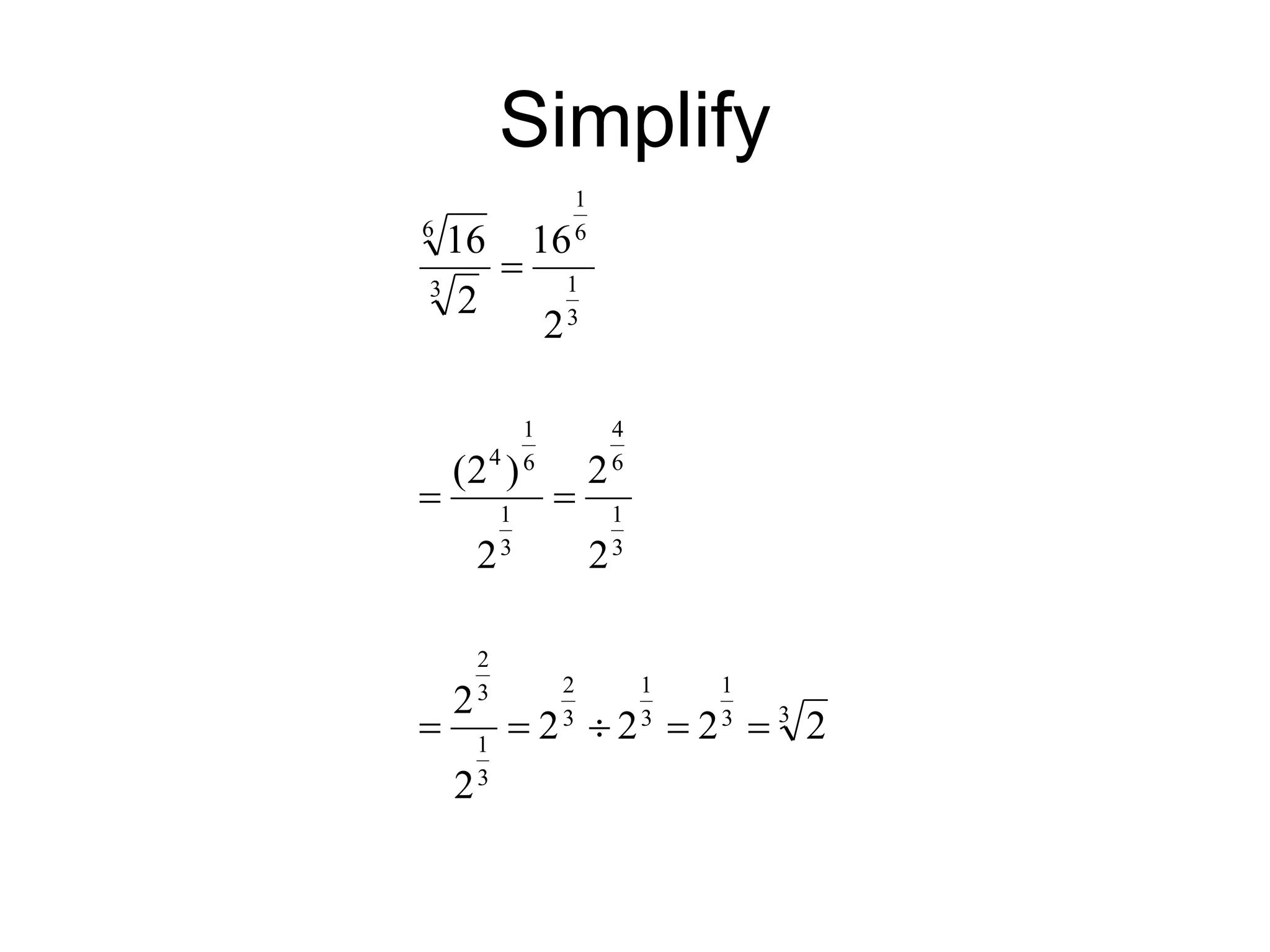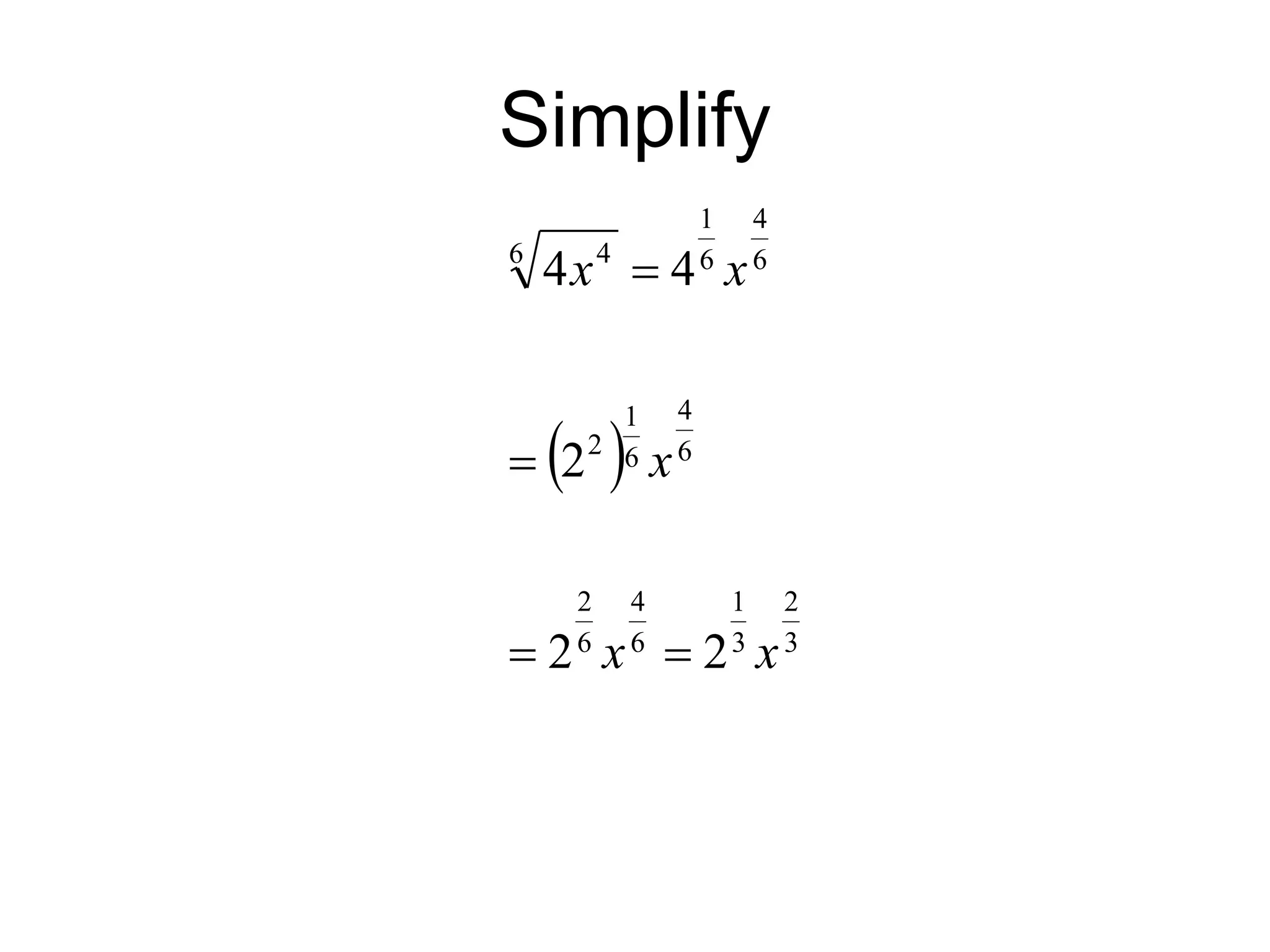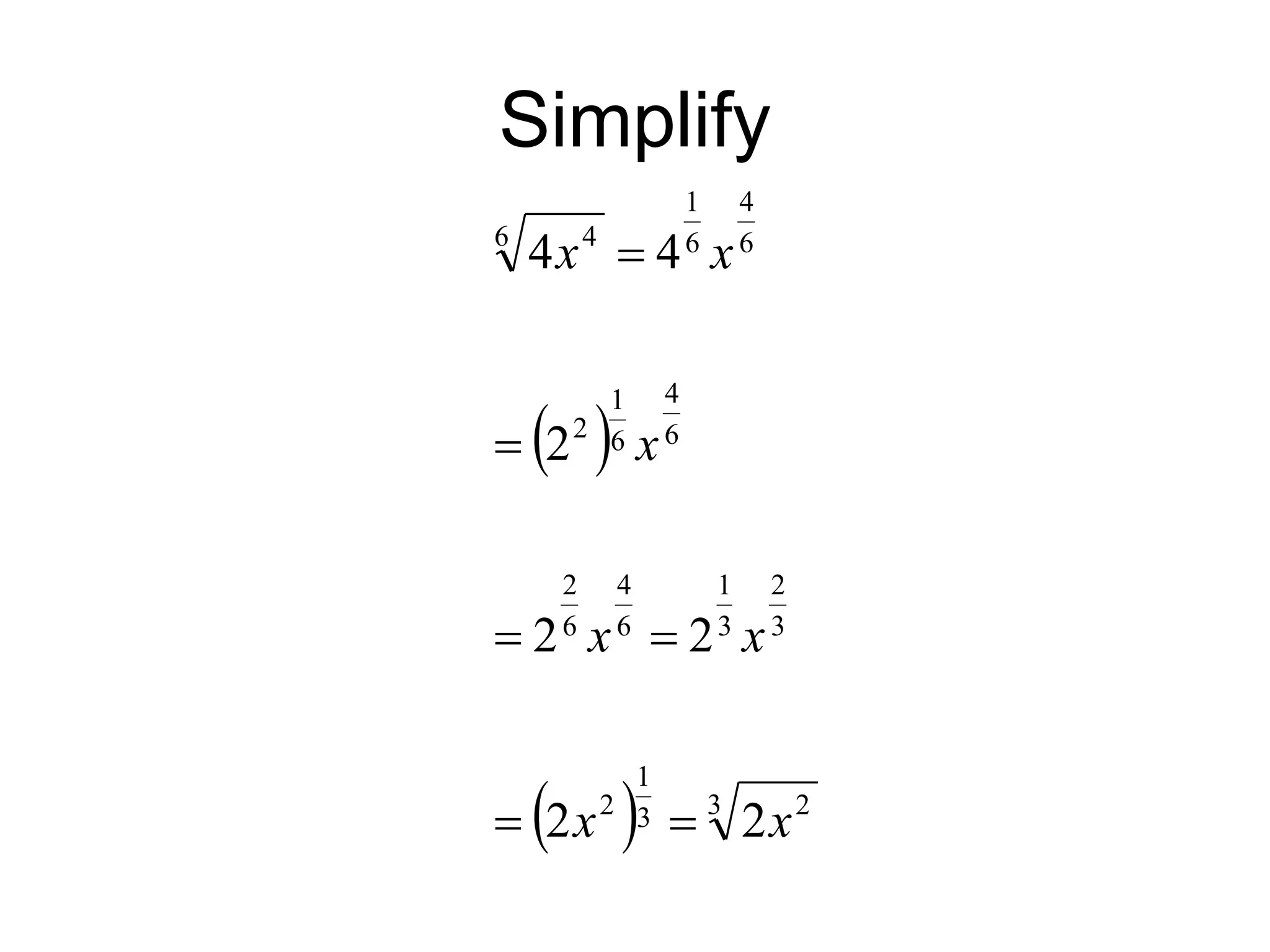The document discusses rational exponents, including how to express numbers with fractional exponents as radical expressions and the implications of negative exponents. It provides various examples of simplifying expressions and emphasizes ensuring that radical expressions remain real. Additionally, the document outlines rules for operations involving exponents and radical forms.