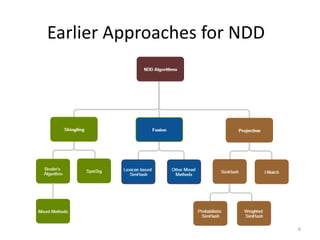
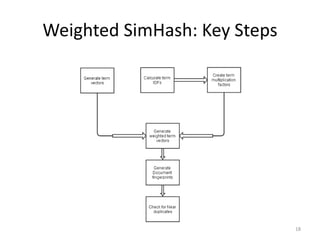
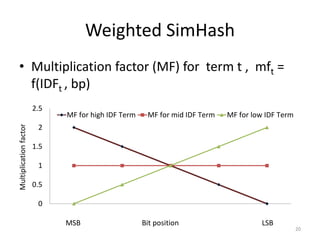
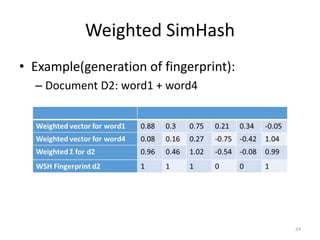
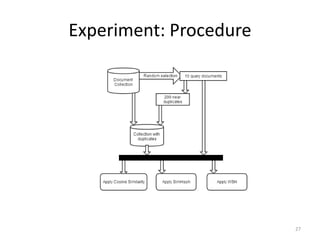
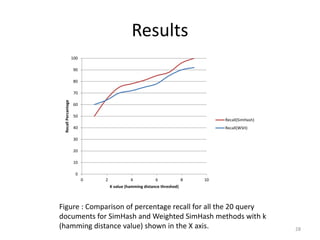
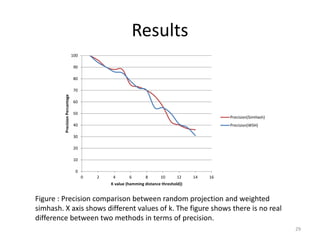
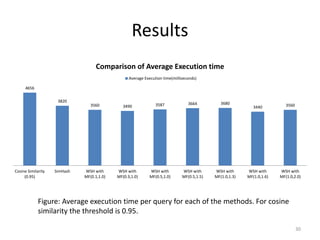
The document presents a method called Weighted Simhash for detecting near duplicate documents, which considers the inverse document frequency (IDF) of terms to improve identification accuracy. It discusses the limitations of previous near-duplicate detection methods and compares Weighted Simhash with traditional approaches like Simhash using experimental results. The findings indicate that while Weighted Simhash achieves better runtime efficiency, its precision and recall performance are comparable to that of Simhash.