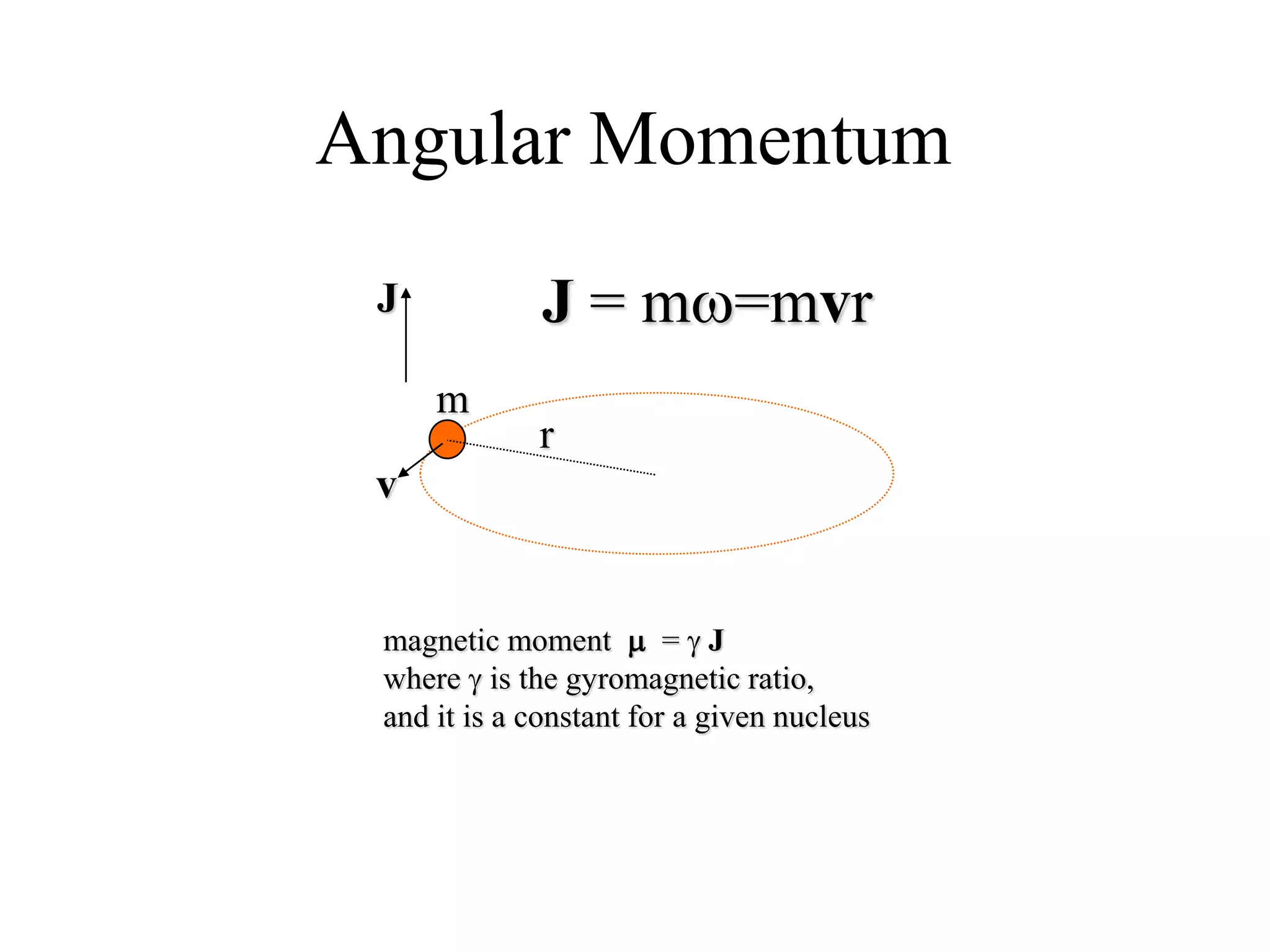
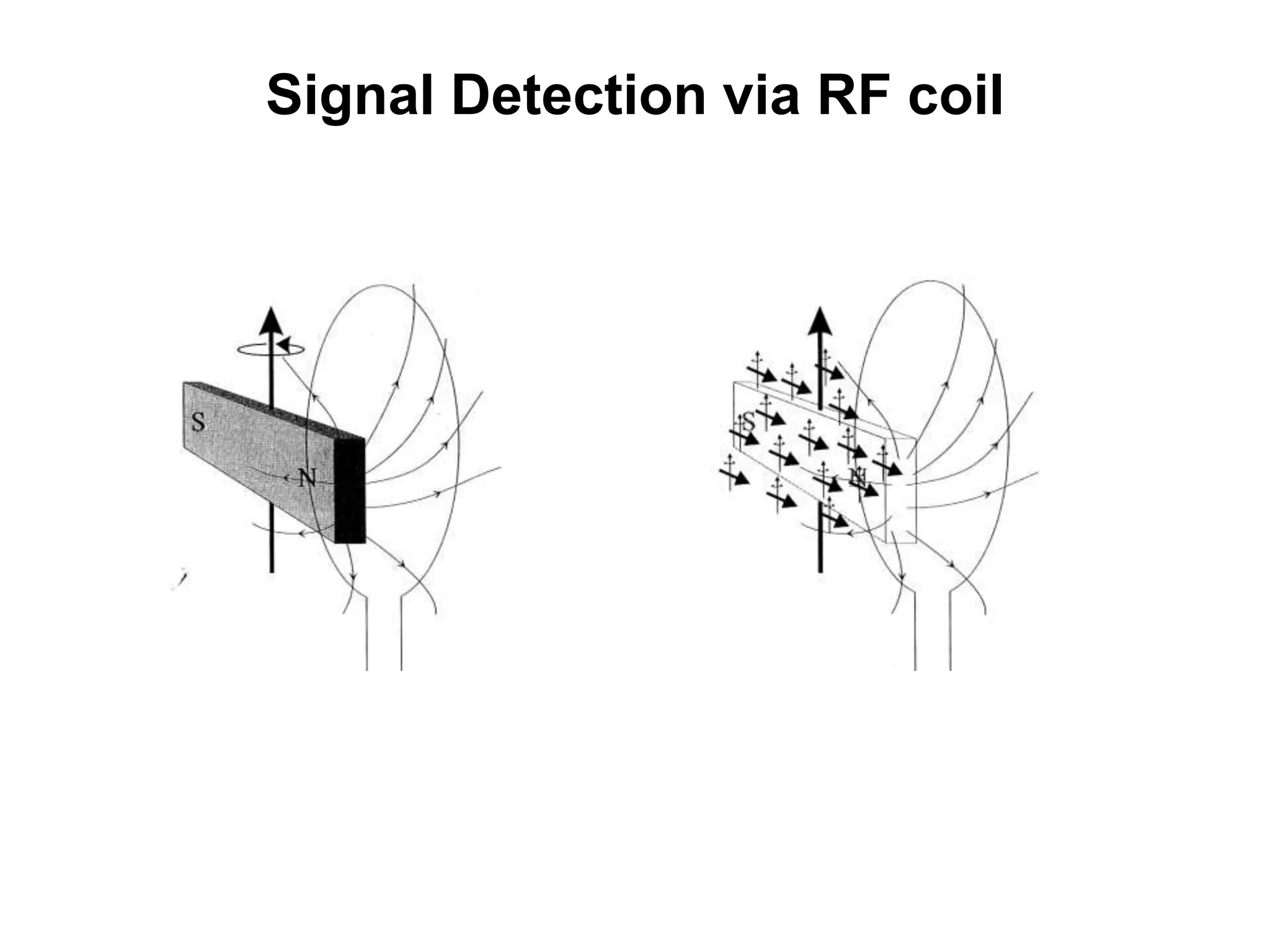
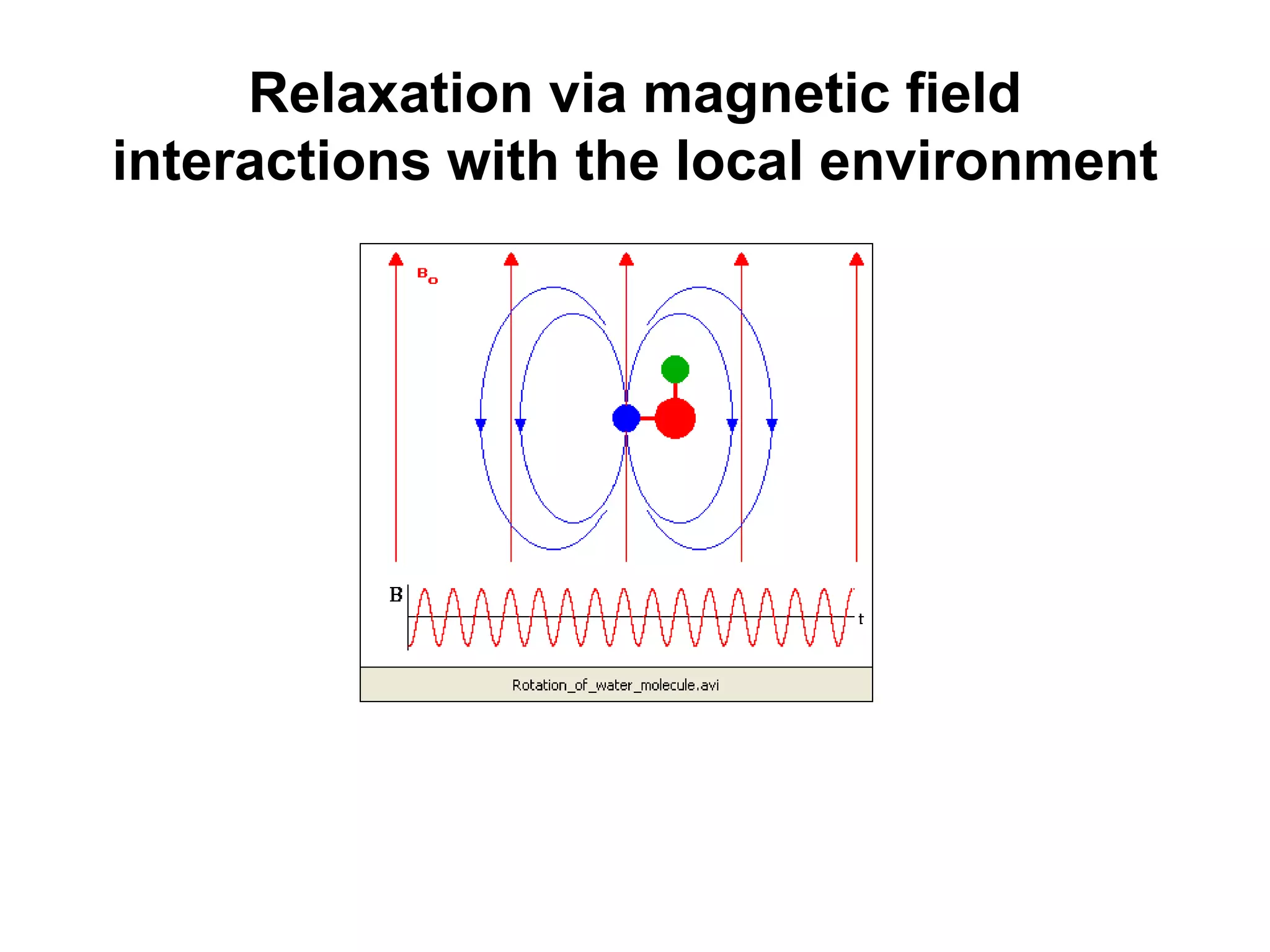
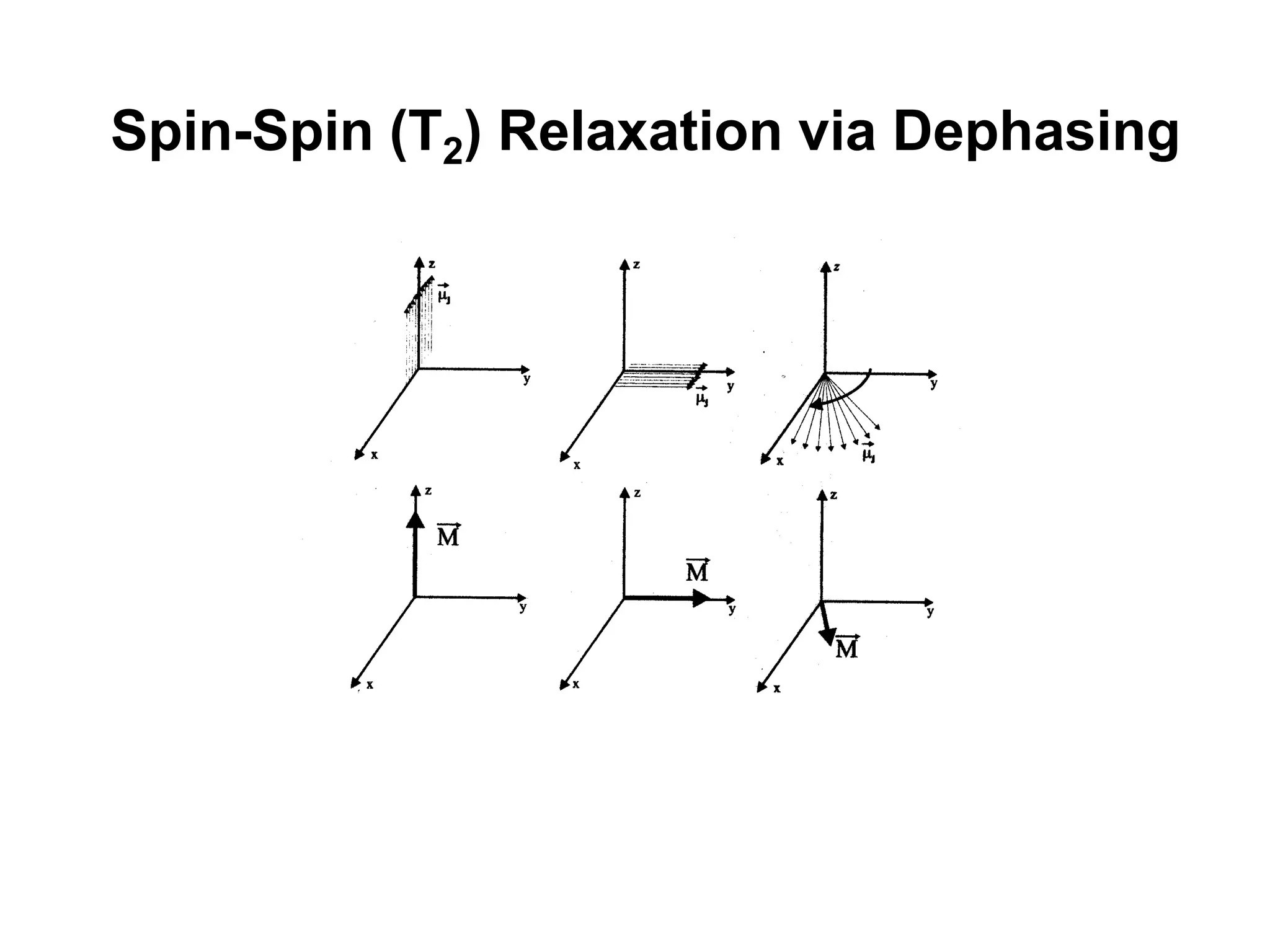
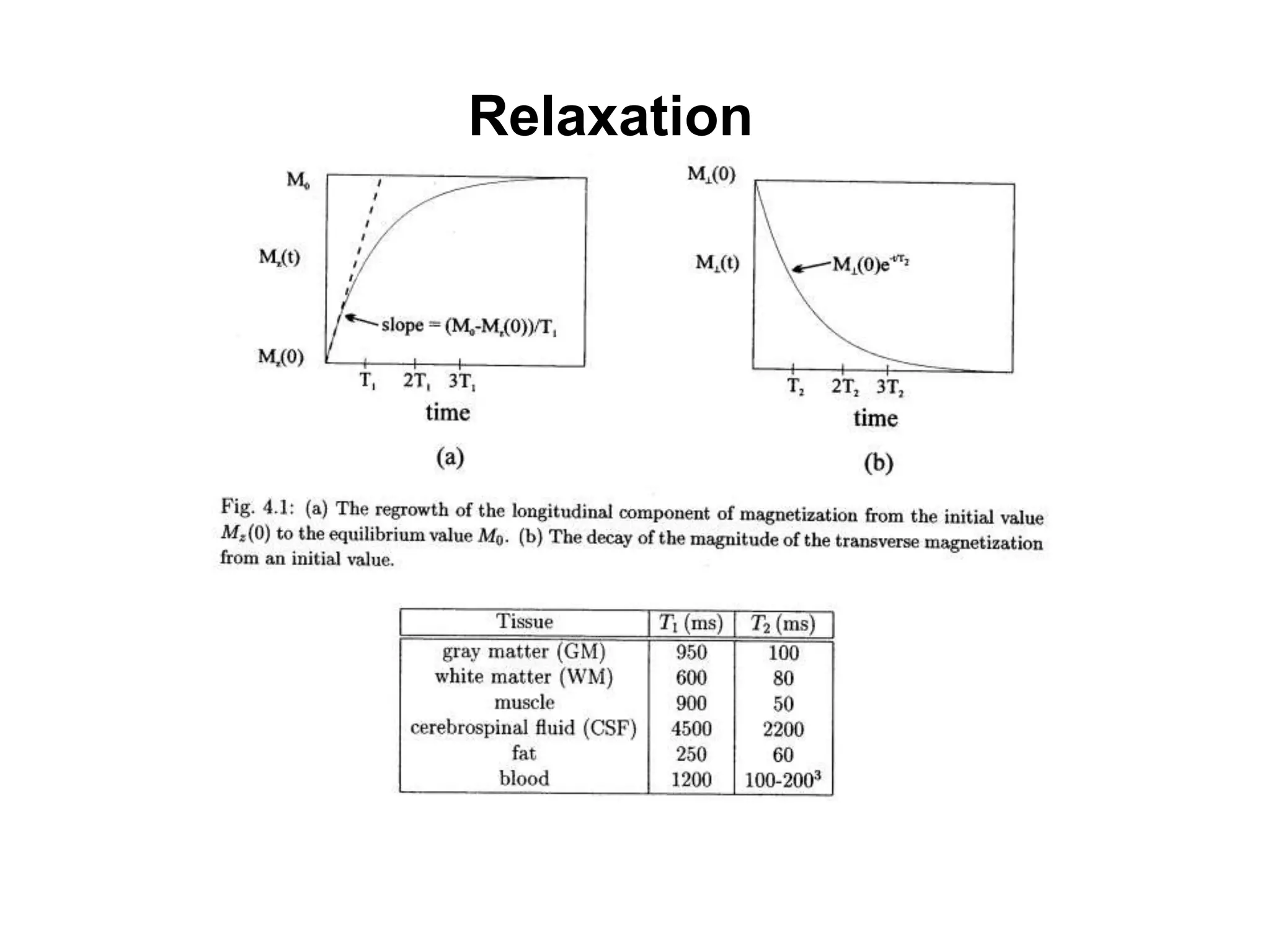
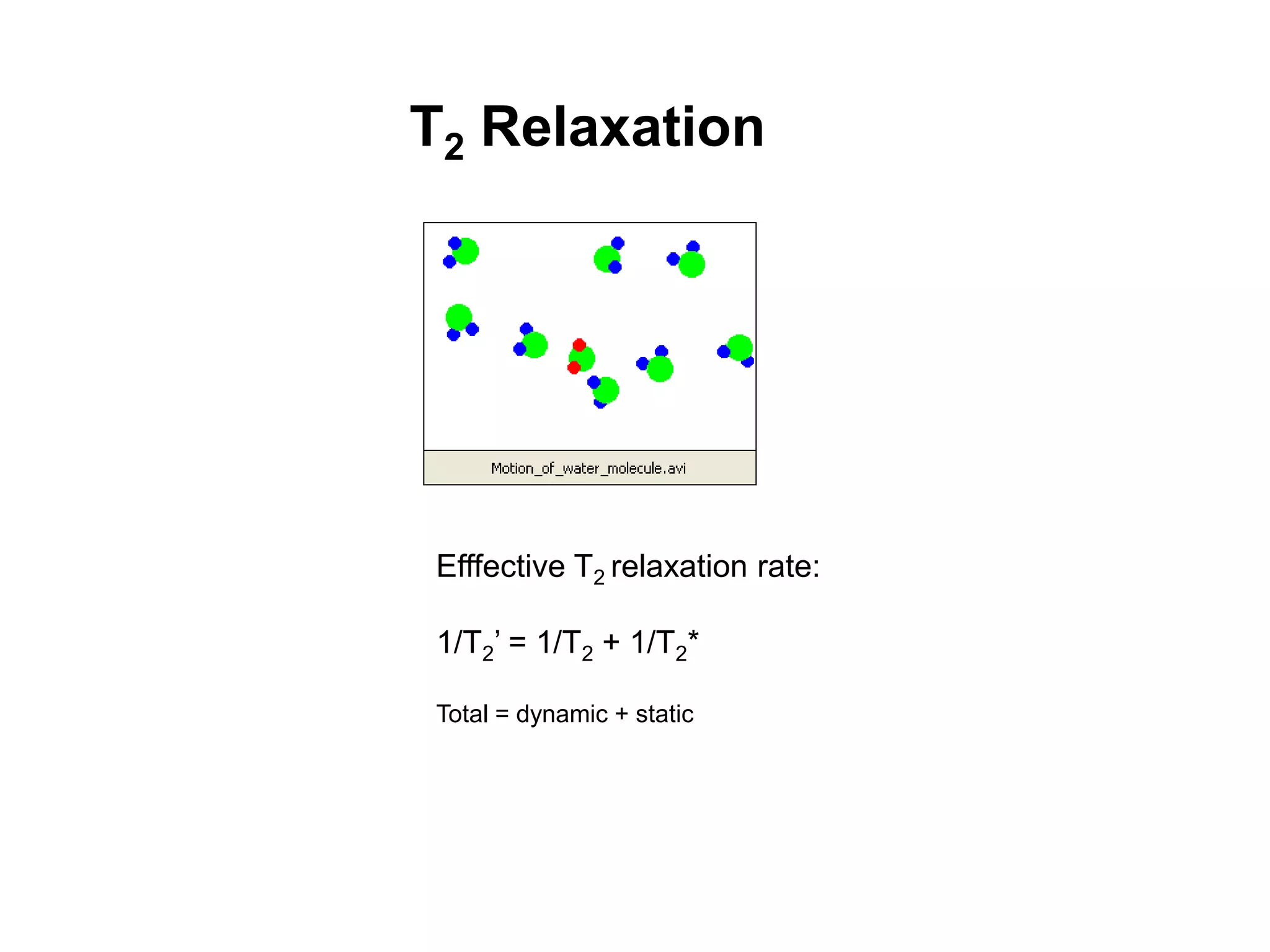
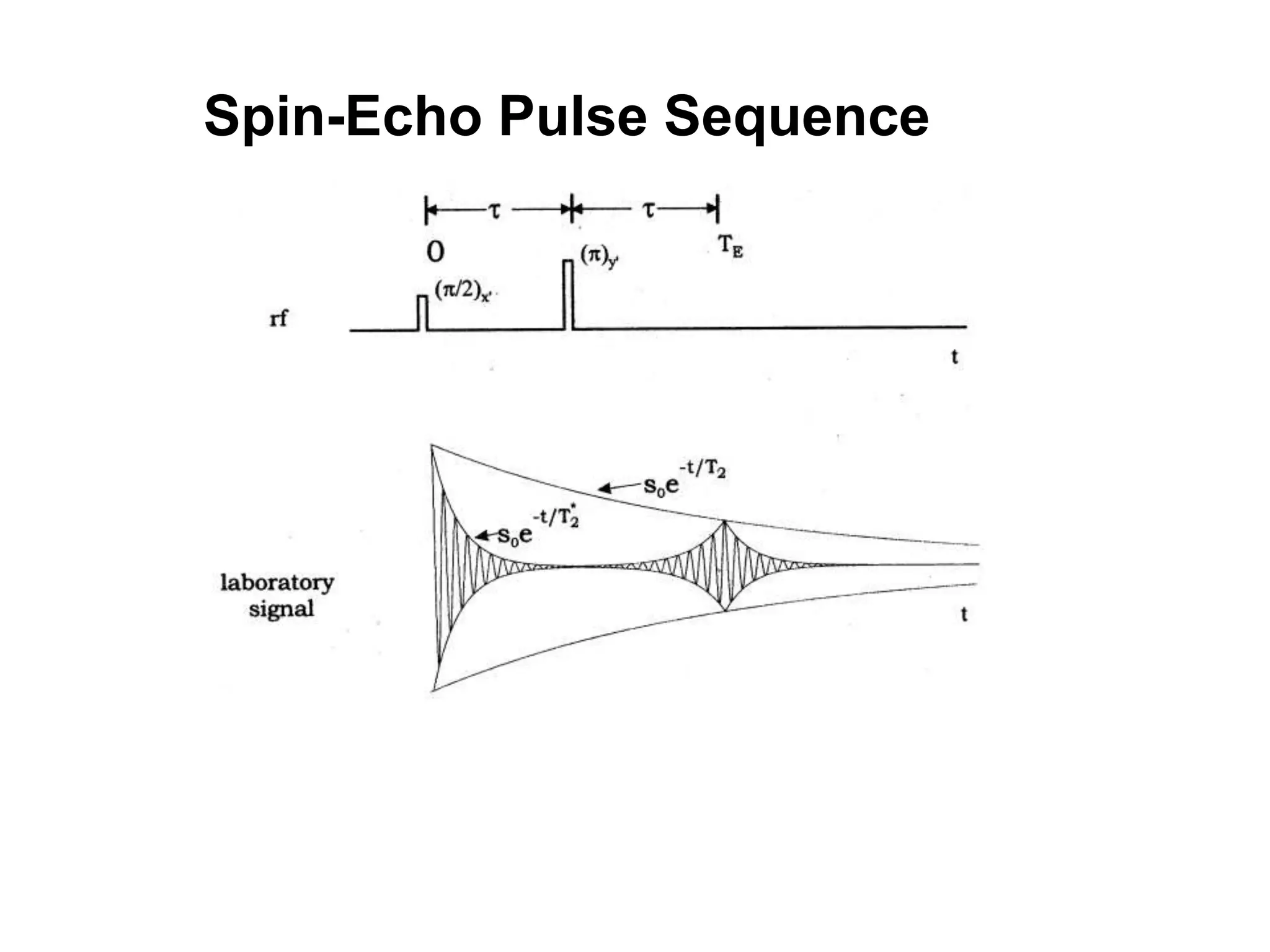
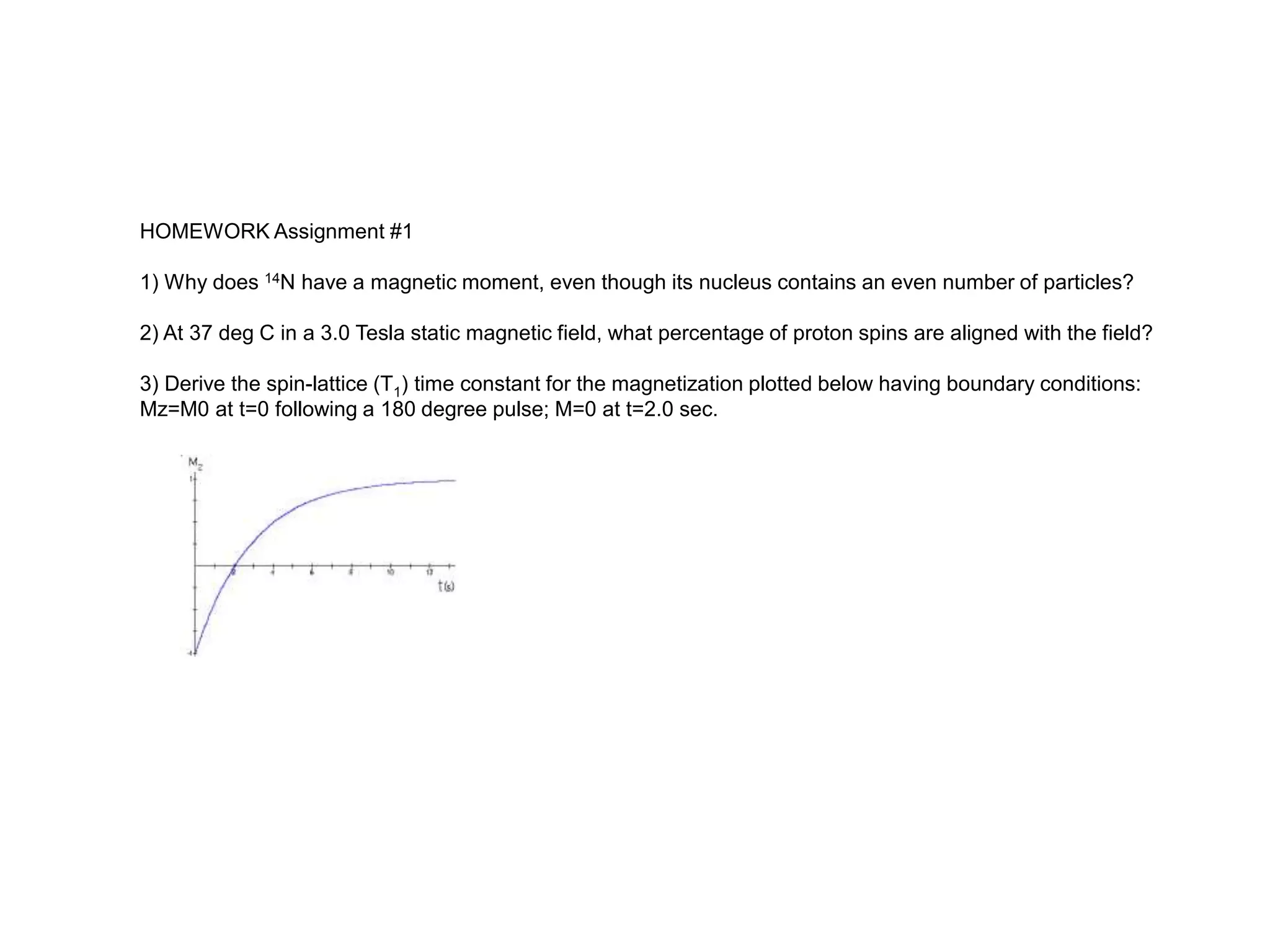
This document provides an introduction to magnetic resonance imaging (MRI) fundamentals. It discusses key topics like nuclear spin phenomenon, magnetic resonance techniques, MRI scanner components, relaxation processes, and pulse sequences. Important historical developments are highlighted, including Nobel Prizes awarded for contributions to MRI and related techniques. References for further reading on introductory MRI physics concepts are also provided.








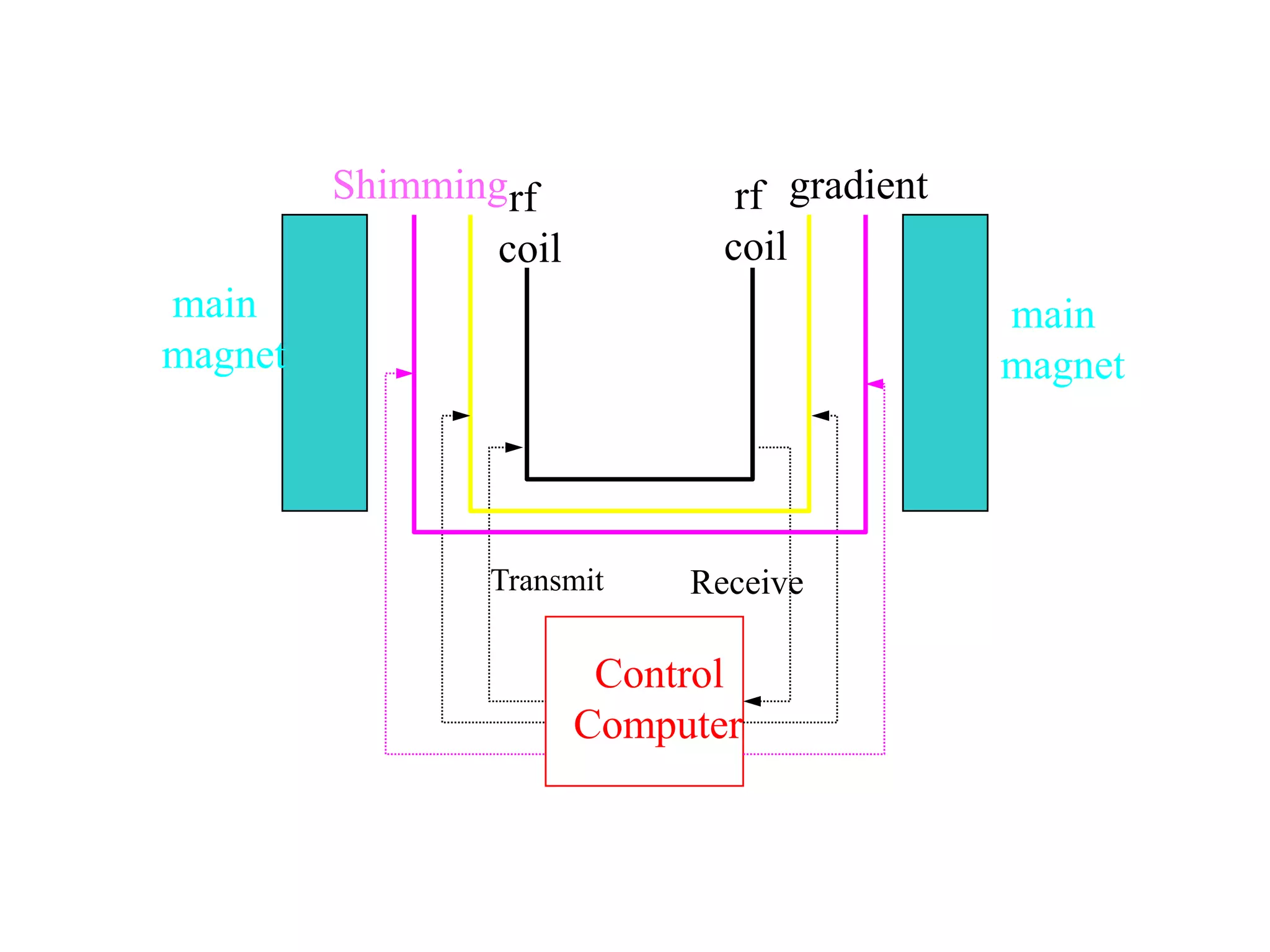
![Main Magnet Field Bo
• Purpose is to align H protons in H2O (little
magnets)
[Little magnets lining up with external lines of force]
[Main magnet and some of its lines of force]](https://image.slidesharecdn.com/mri1-230209112805-90b8830f/75/MRI_1-ppt-10-2048.jpg)