Downloaded 12 times
![#VoxxedVienna @ramtop
Natural Transformations Code
val list = Try {"3".toInt()}.toOption().toList()
//[3]
val fail = Try {"xyz".toInt()}.toOption().toList()
//[]](https://image.slidesharecdn.com/morphisms-180315204216/75/It-s-All-About-Morphisms-36-2048.jpg)
![#VoxxedVienna @ramtop
CandyDispenser
● Code example
● Let’s bring all together
● We have a function Seed (Seed, Candy)→
● Another one (State, Input) State→
● How can we combine them?
● We want
(Dispenser, [Input]) (Dispenser, [Candy])→](https://image.slidesharecdn.com/morphisms-180315204216/75/It-s-All-About-Morphisms-63-2048.jpg)
Uploaded byUberto Barbini
It's All About Morphisms
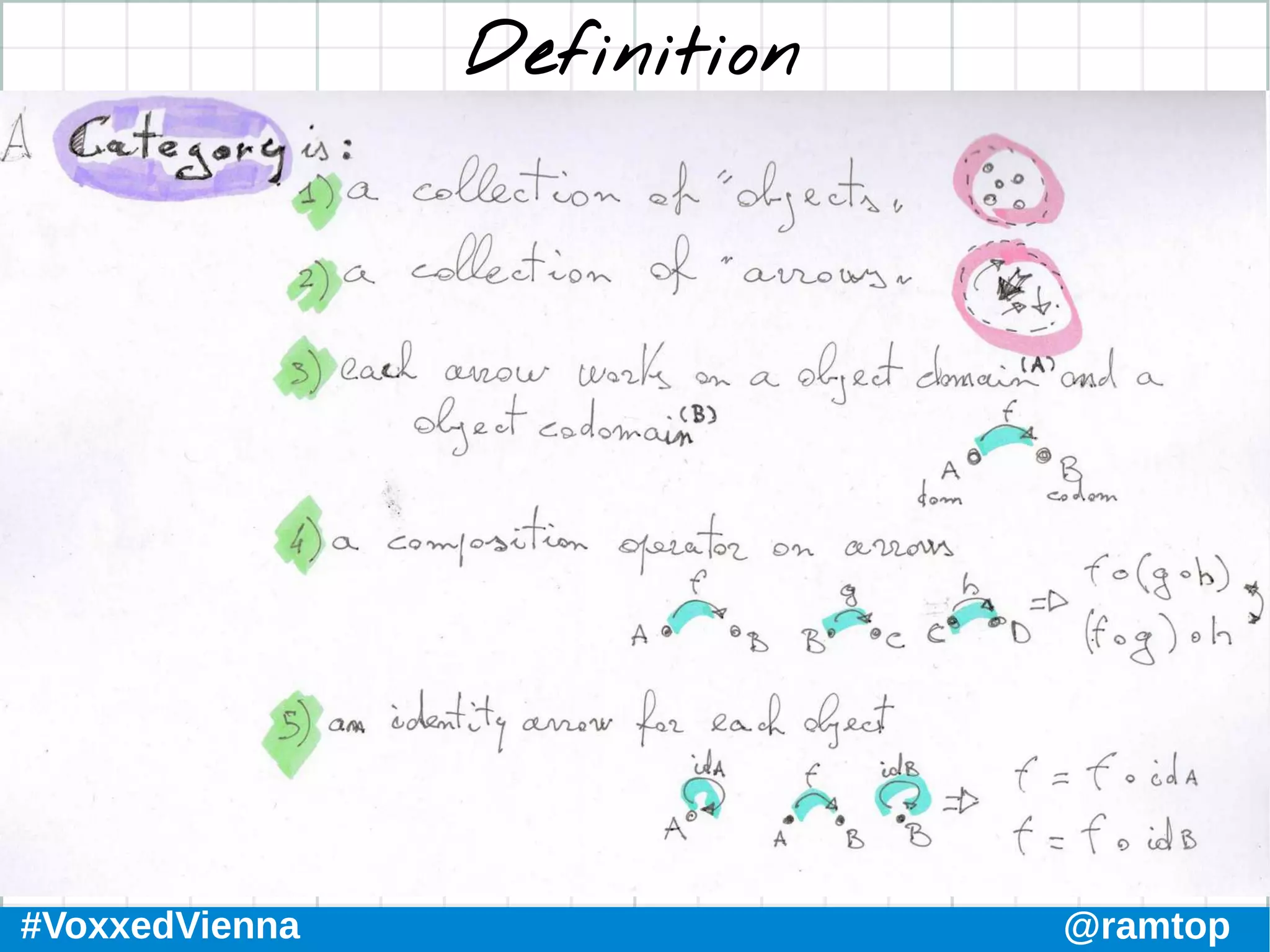
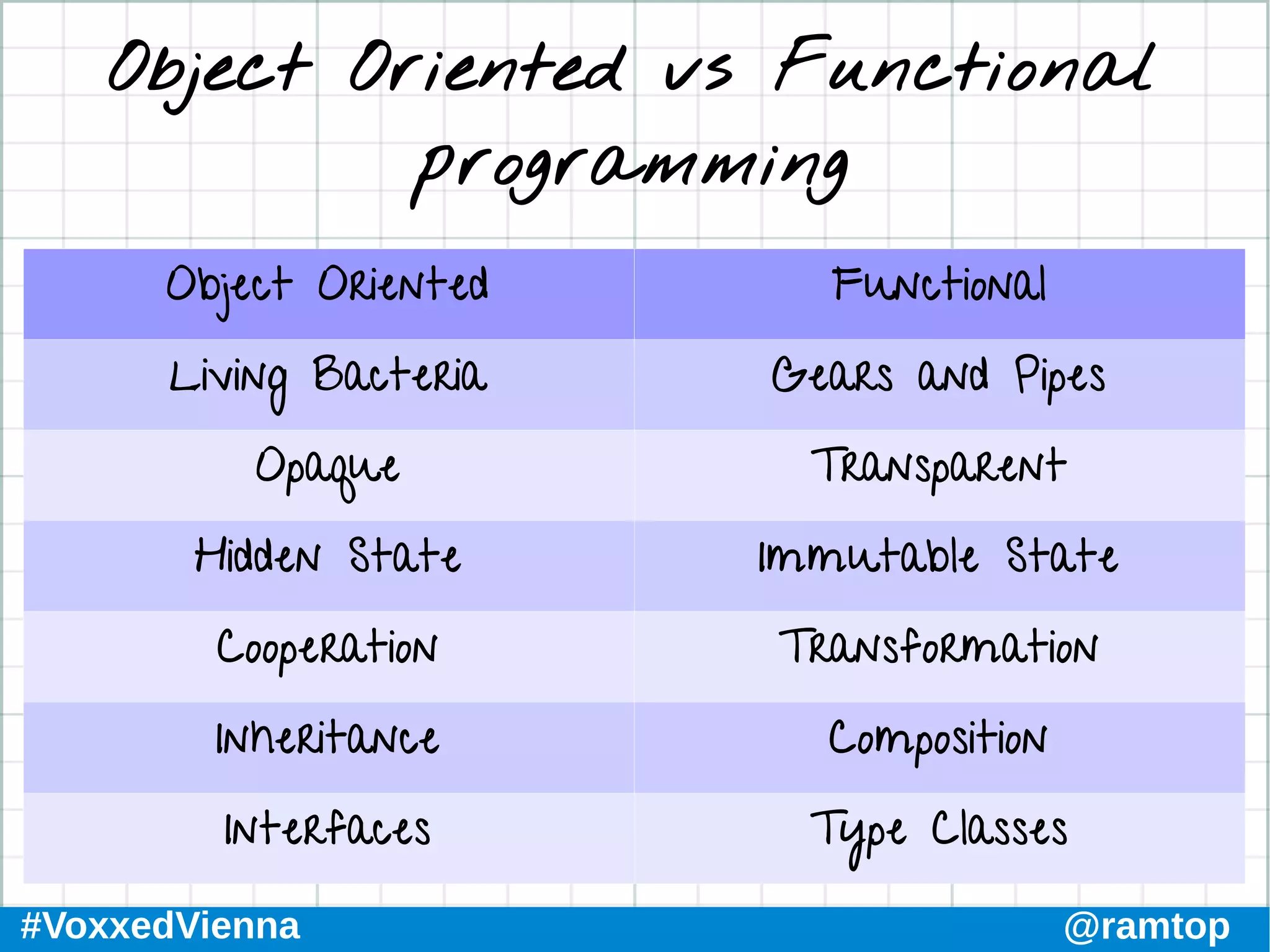
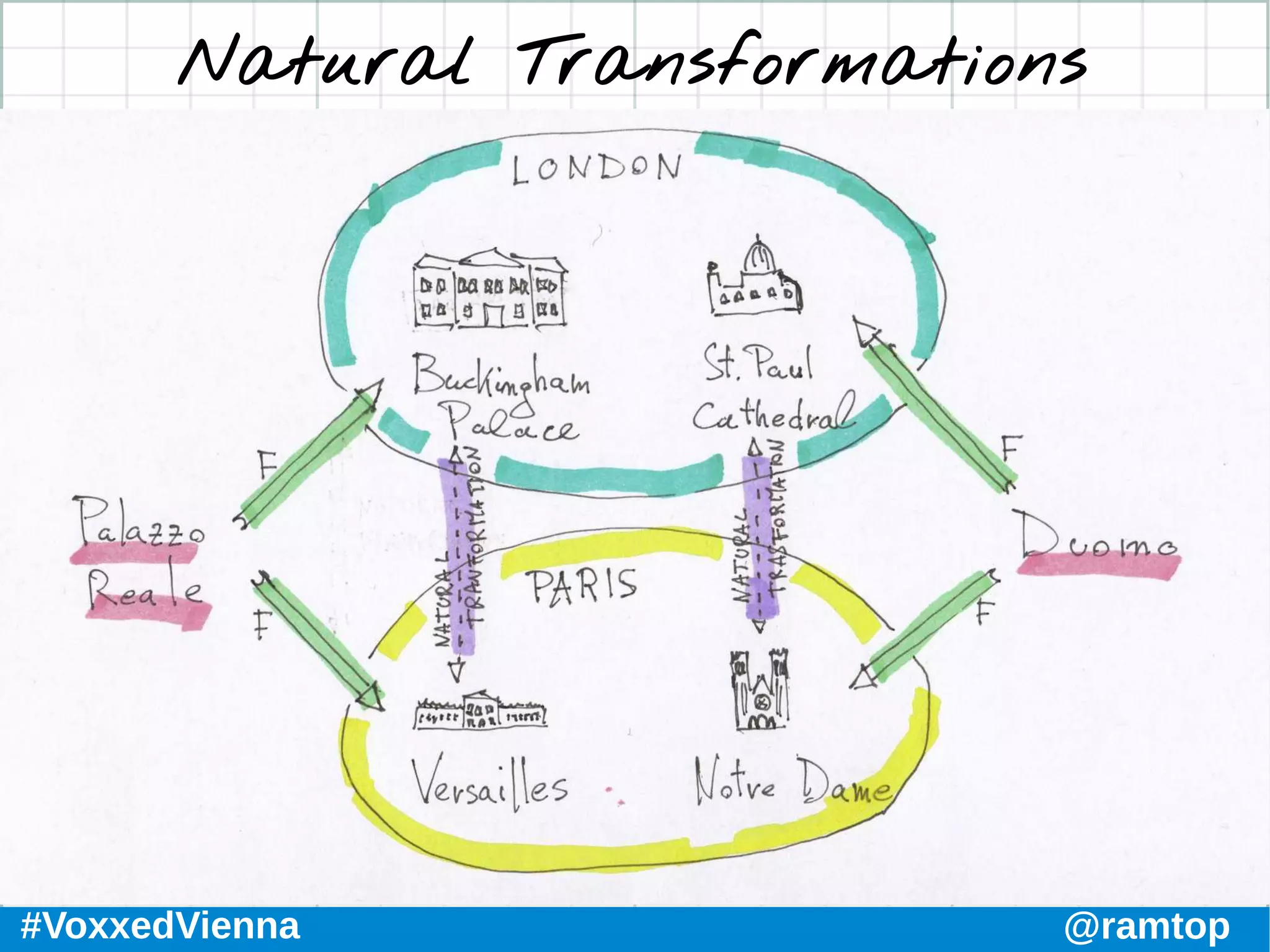
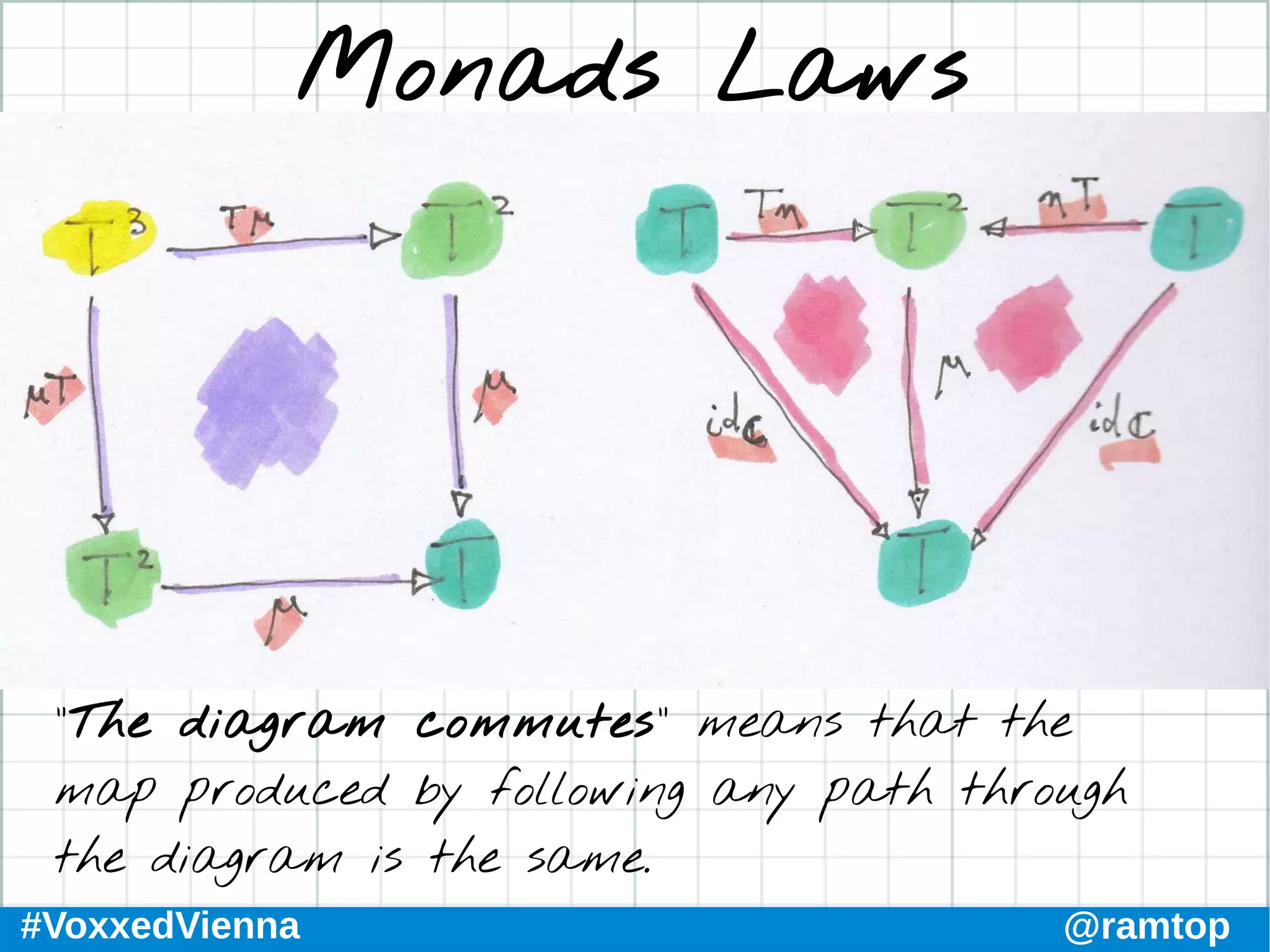
The document discusses the foundations of functional programming and category theory, covering concepts like morphisms, monoids, functors, and monads. It compares functional and object-oriented programming, highlights Kotlin's advantages for functional programming, and explores advanced topics such as natural transformations and higher kinded types. The conclusion emphasizes the importance of understanding these concepts to improve programming practices and develop a deeper understanding of functional programming paradigms.
More Related Content
It's All About Morphisms
- 1. #VoxxedVienna @ramtop It’s AllAbout Morphisms Uberto Barbini
- 2. #VoxxedVienna @ramtop Map ofthis presentation Category Monoid Functor Applicative Monad Natural Transformation The Foundations of Functional Programming
- 3. #VoxxedVienna @ramtop This presentationwill be a success if most of you will not fall asleep
- 4. #VoxxedVienna @ramtop This presentationwill be a success if most of you will not fall asleep As a secondary goal, I hope to encourage people using Functional Programming and studying Category Theory It’s ok if you don’t understand all the first time
- 5. #VoxxedVienna @ramtop What isthis Category thingy? Invented in 1940s “with the goal of understanding the processes that preserve mathematical structure.” “Category Theory is about relation between things” “General abstract nonsense”
- 6. #VoxxedVienna @ramtop Category Theoryis all about Transformations and preserving Properties
- 7.
- 8. #VoxxedVienna @ramtop A CategoryExample Tube Map: Objects stations→ Arrows travel routes→ Each Arrows connect 2 stations Arrow composition is travelling along the line Identity Arrow is staying in the same station
- 9.
- 10. #VoxxedVienna @ramtop Functional Programming isalso a Category Each programming language has a Category: Types are the objects and Functions are the morphisms. Partial functions don’t have a defined return for all inputs, raise Exceptions or never end. It’s Bottom Type ⊥. But we can ignore it for the moment...
- 11. #VoxxedVienna @ramtop Object Orientedvs Functional programming Object Oriented Functional Living Bacteria Gears and Pipes Opaque Transparent Hidden State Immutable State Cooperation Transformation Inheritance Composition Interfaces Type Classes
- 12. #VoxxedVienna @ramtop Advantages ofKotlin over Java for functional programming ● Functions outside classes ● Immutable variables and collections ● Nullable and not-nullable types ● Class extensions ● Tail recursion ● When pattern matching ● Arrow-kt bindinds with coroutines ● Arrow-kt Higher Kinded Types
- 13. #VoxxedVienna @ramtop Two wordsabout Kotlin syntax ● No semicolon! ● String? Is a different type from String ● myFun{println(it)} is equivalent to myFun(x -> println(x)) ● val xy is declaring xy immutable var xy is declaring xy mutable ● User(“Joe”) is equivalent to Java new User(“Joe”)
- 14. #VoxxedVienna @ramtop Ok… butwhy using a Object Oriented Language for Functional Programming at all?
- 15.
- 16.
- 17. #VoxxedVienna @ramtop Purity and Immutability Forthe Category morphisms to work in programming we need Purity and Immutability. What does it mean pure? How can I work only with immutable data? But ultimately everything is converted in assembly which is neither pure nor immutable. We need those quality only for reachable code
- 18. #VoxxedVienna @ramtop Monoid What aboutthe category of morphisms of a category? Are they composable? It’s a Category with a single Object and lots of Morphisms If it is a Category and it has only one Object is a Monoid
- 19. #VoxxedVienna @ramtop Sum isa Monoid
- 20. #VoxxedVienna @ramtop London TubeMap is a Monoid! (if you squint hard enough)
- 21. #VoxxedVienna @ramtop Programming withMonoids A type class with two methods combine monoid append→ empty neutral element→ (x <> y) <> z = x <> (y <> z) -- associativity empty <> x = x -- left identity x <> empty = x -- right identity
- 22. #VoxxedVienna @ramtop Type Classvs Interface ● Interfaces “unify” different types: Cat and Dogs can be treated as Animals ● Type Classes “group” types with similar behaviour, without hiding their types: Cats and Dogs can both mate but cats can mate only with cats and dogs with dogs ● As an example, let’s consider the Equals method in Java
- 23. #VoxxedVienna @ramtop About TypeclassInstances ● Typeclasses works with instances ● List is not a Monoid nor a Functor nor a Monad but it has an (or more) instance of Monoid one of Functor and one of Monad ● Technically we implement instances as an interface with a singletons specific implementation. ● We can have different implementation for difference in evaluation, for example because of concurrency
- 24. #VoxxedVienna @ramtop Monoids Code @Testfun emptyLaw() { val StringMonoid = monoid<String>() //the instance val empty = StringMonoid.empty() assertEquals("a", StringMonoid.combine(empty, "a")) assertEquals("a", StringMonoid.combine("a", empty)) } @Test fun associativityLaw() { assertEquals(12, 3.combine( 4.combine(5) )) assertEquals(12, (3.combine(4)).combine(5)) } @Test fun combineAll() { val word = listOf("Λ", "R", "R", "O", "W").combineAll() assertEquals("ΛRROW", word) }
- 25. #VoxxedVienna @ramtop Functors Functors canmap both objects (types) and morphism (functions) between two categories Functors map must preserve the structure and some properties But can also work inside the same category (Endofunctors)
- 26. #VoxxedVienna @ramtop Functors areTransformers Functors are the single most important concept of this talk
- 27. #VoxxedVienna @ramtop Functor Laws Functoris a TypeClass with a Map function that works like this. Id is the identity function. map id x = x map (g <> f) = map g <> map f) Passing the ID function must return the original value Map must honour associativity of two functions
- 28.
- 29. #VoxxedVienna @ramtop Endofunctors ● Inprogramming we only work with Endofunctors in the Category of our types ● Endofunctor map a => F a where F a is a type constructor in the same category of a (the type system category) ● Endofunctors are very important because we can compose them!
- 30. #VoxxedVienna @ramtop Higher KindedTypes ● Generics === Type constructors ● List<A> abstracts over A ● In Java we cannot abstract at more than one level like List<A<B>> or ignoring the second level List<A<?>> ● But in Functional programming makes sense generalise over things like: List<A> + fun(A -> B) = List<B> List<Try<A>> + fun(Try<A> -> B)= List<B> etc.
- 31. #VoxxedVienna @ramtop Try Functor "6".toInt()+ 1 "nope".toInt() + 1 //NumberFormatException Try {"6".toInt()}.map { it + 1 } //using instance would be Try.functor().map(... //Try.Success(7) Try {"nope".toInt()}.map { it + 1 } //Try.Failure(Exception...)
- 32. #VoxxedVienna @ramtop Functors arealso Forklifts val lifted = Try.functor().lift {x:String -> x.toInt()} lifted(Try.Success("6")) //Try.Success(6) lifted(Try.Success("42")) //Try.Success(42) Lift a function from A → B to F<A> → F<B>
- 33. #VoxxedVienna @ramtop Reader: AFunctor on functions Val userId = 123 val reader = Reader{dbUrl:String -> DbConn(dbUrl)} val name = reader.run("myDbConn") .map{it.getUser(userId) } .map{it.name} .value() //"Joe"
- 34. #VoxxedVienna @ramtop Natural Transformations Anatural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Transforming Data Functions→ Transforming Functions Functors→ Transforming Functors Natural Transformations→
- 35.
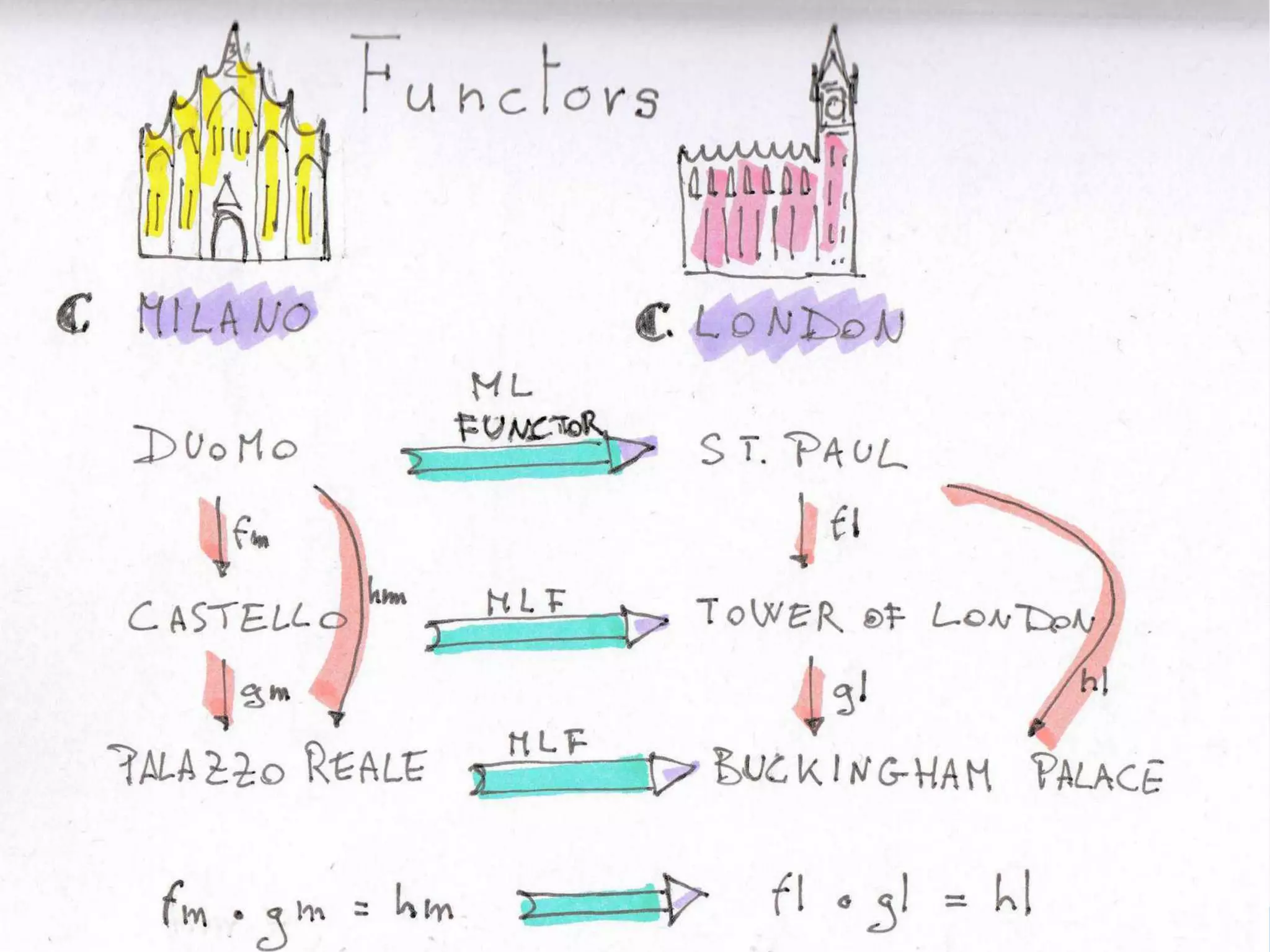
- 36. #VoxxedVienna @ramtop Natural TransformationsCode val list = Try {"3".toInt()}.toOption().toList() //[3] val fail = Try {"xyz".toInt()}.toOption().toList() //[]
- 37. #VoxxedVienna @ramtop Monoid +Functor Monoid is about combining and reducing We can imagine 2 ways to combine 2 functors F + F = F F<f> map F<a> = F<f(a)> or F * F = F flatmap (a → F<a → F<a>>) = F a
- 38. #VoxxedVienna @ramtop Applicative Functors ●So far we considered only functions with 1 parameter ● We can combine a value inside a Functor with a function inside another Functor ● If the function want more than 1 param it will return a function with x-1 params ● Applicative can apply F<A->B> to F<A> to create F<B> or F<A,B ->C> to F<A> and F<B> to create F<C>
- 39. #VoxxedVienna @ramtop Try ApplicativeFunctor val tryHarder = Try.applicative().tupled( Try { "3".toInt() }, Try { "5".toInt() }, Try { "nope".toInt() } ) //Failure(exception=NumberFormatException… val tryHarder = Try.applicative().tupled( Try { "3".toInt() }, Try { "5".toInt() }, Try { "15".toInt() }) //Success(value=Tuple3(a=3, b=5, c=15))
- 40. #VoxxedVienna @ramtop Monads ● Whatabout a category of (endo)functors? ● Some functors have a monoid instance, others not. ● Ok now how we call all those Endofunctors with a Monoid instance?
- 41. #VoxxedVienna @ramtop Monad Recipe: 1Category of Endofunctors 2 Natural Transformations: Unit and Multiplication
- 42. #VoxxedVienna @ramtop Monads Laws "Thediagram commutes" means that the map produced by following any path through the diagram is the same.
- 43. #VoxxedVienna @ramtop Monads Zoo AllMonads are also Functors and Applicative, but the opposite is not true. Each Monad as it’s specific logic on top of the Monads Laws These are already available in many libraries but you can extend and create your own. ● Option ● Try ● List ● Either ● Reader ● Writer ● State ● IO ● Free
- 44.
- 45. #VoxxedVienna @ramtop Monads Binding Fromhere: val university: IO<University> = getStudent("John Smith").flatMap { student -> getUniversity(student.universityId).flatMap { university -> getDean(university.deanId) } } To here: val university: IO<University> = IO.monad().binding { val student = getStudent("John Smith").bind() val university = getUniversity(student.universityId).bind() val dean = getDean(university.deanId).bind() dean }
- 46. #VoxxedVienna @ramtop Reader MonadBindings fun getUserFromContext(userId:String) = Reader<DbConn, User>{c -> c.getUser(userId)} val res = Reader().monad<DbConn>().binding{ val u1 = getUserFromContext("Frankie").bind() val u2 = getUserFromContext("Jonnny").bind() "$u1 & $u2" }.ev().run(DbConn("myDbUrl")) //User(name=Frankie) & User(name=Jonnny)
- 47. #VoxxedVienna @ramtop How touse morphisms in real world programs?
- 48. #VoxxedVienna @ramtop "Rather thanthinking about function purity as a goal, you have to think about which properties you want your program to preserve." @raulraja Perfectly Pure Programs are Perfectly Useless
- 49. #VoxxedVienna @ramtop Purity Bubbles+ Events = Actors
- 50. #VoxxedVienna @ramtop Conclusions: why functionalprogramming? For sure is not because the code is easier to read!
- 51. #VoxxedVienna @ramtop Conclusions: why functionalprogramming? More composition Less boilerplate Less repetitions Less bugs Less need for tests Easier concurrency Less sugar Different thinking Performance issues Complex state More precision Different testing style VS
- 52. #VoxxedVienna @ramtop Conclusions: why studyingCT? Morphisms allows you to work at compile time with your Domain Knowledge Learn how to compose functions and preserve properties Monads and other typeclasses should emerge from your code, not the other way round Learn a common terminology and the reasons behind that
- 53. #VoxxedVienna @ramtop To learnmore Notes on category theory in the context of (functional) programming https://github.com/jwbuurlage/category-theory- programmers Category Theory for Programmers bartoszmilewski.com Learn You A Haskell For Great Good http://learnyouahaskell.com Hardcore Mathematical stuff: https://www.youtube.com/user/TheCatsters nLab https://ncatlab.org/nlab/show/HomePage
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60. #VoxxedVienna @ramtop Monads Transformers ●Monads don’t compose
- 61. #VoxxedVienna @ramtop Kleisli Arrows Originalproblem: Monads don’t allow for concurrency Arrows can be useful in Reactive Functional Programming Kleisli is a type of Arrow for a Monadic context It’s old ReaderT actually
- 62.
- 63. #VoxxedVienna @ramtop CandyDispenser ● Codeexample ● Let’s bring all together ● We have a function Seed (Seed, Candy)→ ● Another one (State, Input) State→ ● How can we combine them? ● We want (Dispenser, [Input]) (Dispenser, [Candy])→
- 64. #VoxxedVienna @ramtop Adjoint Functors FunctorF from category D to C Functor G from C to D Every adjunction 〈 F, G, ,ε η 〉 gives rise to an associated monad 〈 T, ,η μ 〉 in the category D.