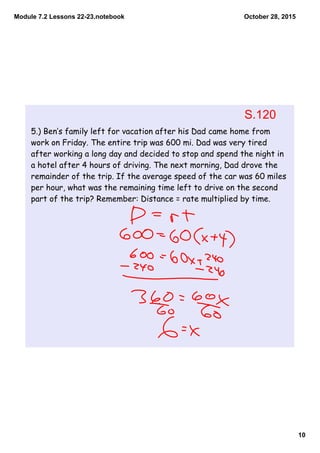This document outlines the homework, lessons, and exercises for Module 7.2 Lessons 22-23. It includes: - The homework assignment of problems 1-4, 6-7 from Lesson 23 and the end of module exam on 10/30. - Examples of solving equations using the equation method, inverse operations, and modeling with tape diagrams. - Practice problems such as solving for the number of hours swimming and calculating original prices. - Closing questions about solving equations and the role of inverse operations.

1. Module 7.2 Lessons 22­23.notebook
1
October 28, 2015
Homework:
• Lesson 23 Problem Set
#1-4, 6, 7
• End of Module 2 Exam
Friday 10/30/15
Module 7.2, Lesson 22-23
Do Now:
Exit Ticket For Lesson 17
Solving Equations
Using Algebra
10/28/15

2. Module 7.2 Lessons 22­23.notebook
2
October 28, 2015
Exit Ticket Lesson 17

3. Module 7.2 Lessons 22­23.notebook
3
October 28, 2015
Homework Answers S.118

4. Module 7.2 Lessons 22­23.notebook
4
October 28, 2015
S.119

5. Module 7.2 Lessons 22­23.notebook
5
October 28, 2015
Equation Method
S.119

6. Module 7.2 Lessons 22­23.notebook
6
October 28, 2015
Solve Equation
Does your answer make sense in the context of the problem?
Why?
n + n + 20 + 15 + 10 + 12 = 137

7. Module 7.2 Lessons 22­23.notebook
7
October 28, 2015
Let x = _____________________________The number of hours swimming each morning
Equation:
S.119

8. Module 7.2 Lessons 22­23.notebook
8
October 28, 2015
S.120

9. Module 7.2 Lessons 22­23.notebook
9
October 28, 2015
3. Claire‛s mom found a very good price on a large computer
monitor. She paid $325 for a monitor that was only $65
more than half the original price. What was the original
price?
S.120

10. Module 7.2 Lessons 22­23.notebook
10
October 28, 2015
5.) Ben‛s family left for vacation after his Dad came home from
work on Friday. The entire trip was 600 mi. Dad was very tired
after working a long day and decided to stop and spend the night in
a hotel after 4 hours of driving. The next morning, Dad drove the
remainder of the trip. If the average speed of the car was 60 miles
per hour, what was the remaining time left to drive on the second
part of the trip? Remember: Distance = rate multiplied by time.
S.120

11. Module 7.2 Lessons 22­23.notebook
11
October 28, 2015
S.123

12. Module 7.2 Lessons 22­23.notebook
12
October 28, 2015
S.124

13. Module 7.2 Lessons 22­23.notebook
13
October 28, 2015
S.125

14. Module 7.2 Lessons 22­23.notebook
14
October 28, 2015
S.125

15. Module 7.2 Lessons 22­23.notebook
15
October 28, 2015
S.126

16. Module 7.2 Lessons 22­23.notebook
16
October 28, 2015
Closing Questions
• What do we mean when we say “solve the equation 6 −8=40"?
• What property allows us to add 8 to both sides?
• What role do inverse operations play in solving this equation,
and how can you model its use with the tape diagram?

17. Module 7.2 Lessons 22­23.notebook
17
October 28, 2015
S.116