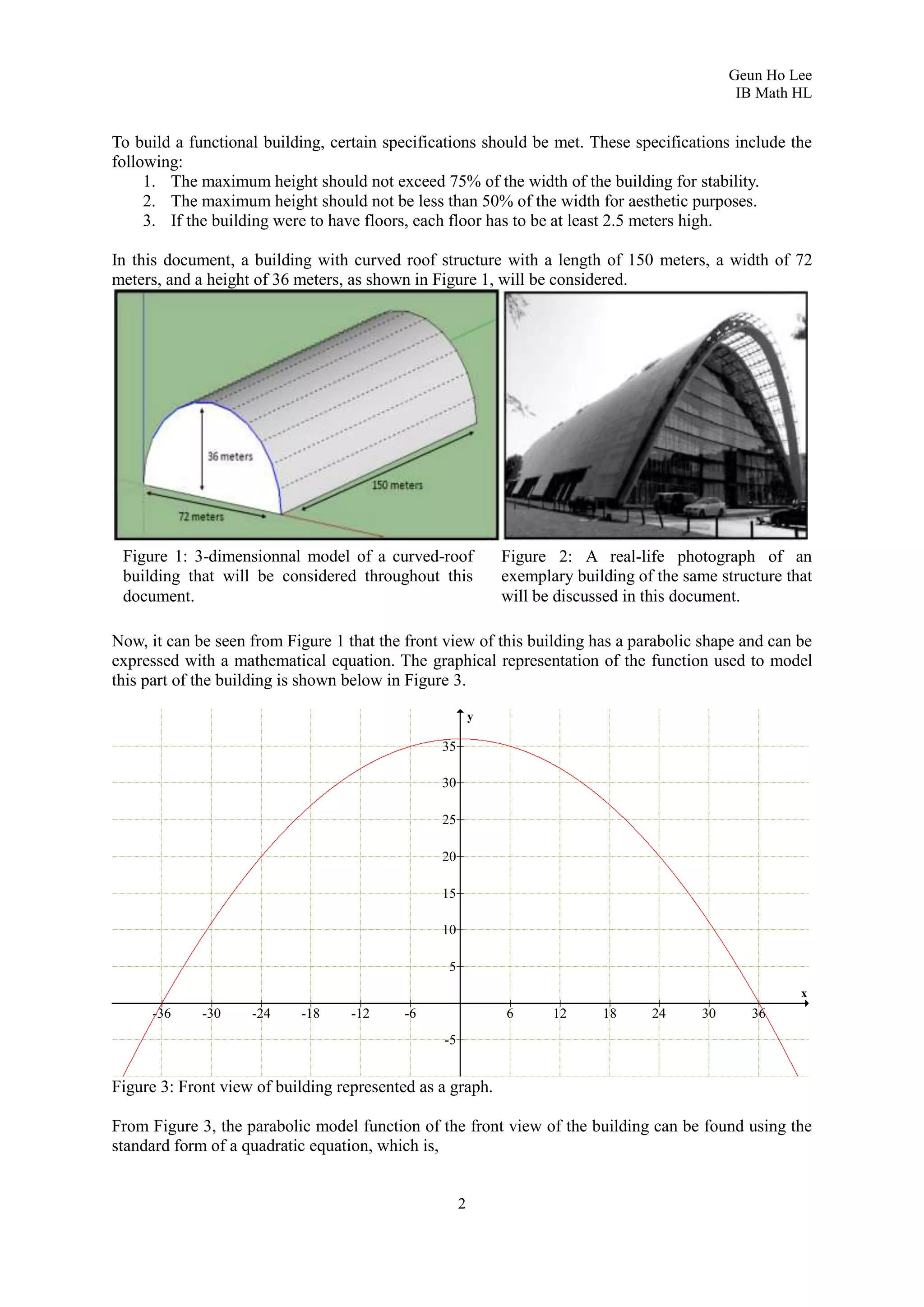
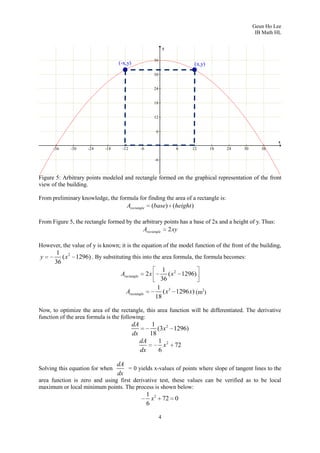
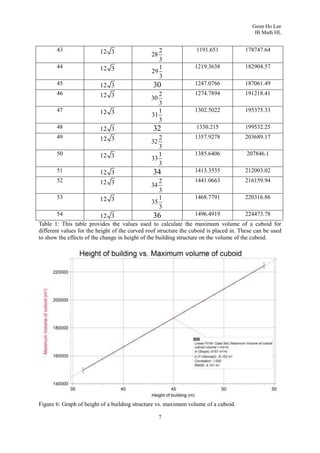
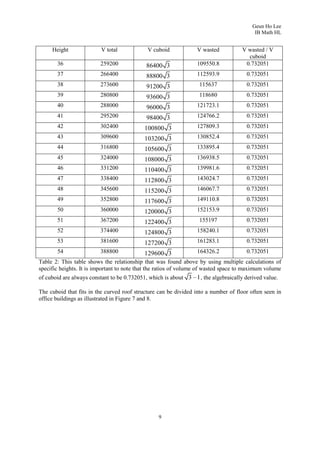
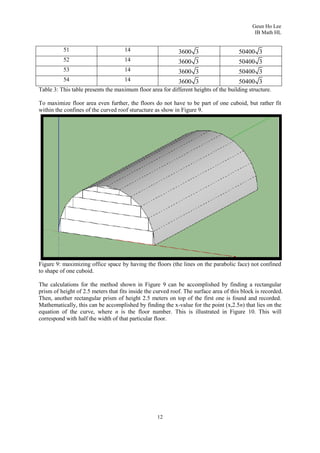
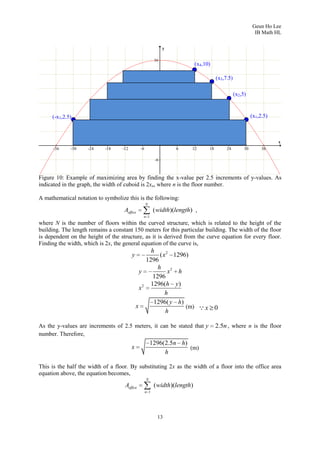
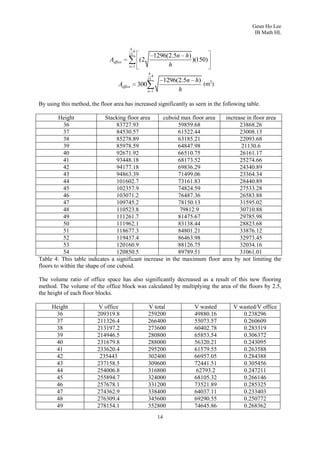
1. The document discusses specifications for building stability and aesthetics, including a maximum height of 75% and minimum of 50% of the width. 2. It analyzes a specific building with a curved roof that is 150m long, 72m wide, and 36m high, modeling its front face as a parabolic function. 3. To find the maximum volume cuboid that can fit inside, it derives the area function of a rectangle on the parabolic face, finds where it is maximized, and calculates the maximum volume as 86,400 cubic meters.

1. Geun Ho Lee
IB Math HL
To build a functional building, certain specifications should be met. These specifications include the
following:
1. The maximum height should not exceed 75% of the width of the building for stability.
2. The maximum height should not be less than 50% of the width for aesthetic purposes.
3. If the building were to have floors, each floor has to be at least 2.5 meters high.
In this document, a building with curved roof structure with a length of 150 meters, a width of 72
meters, and a height of 36 meters, as shown in Figure 1, will be considered.
Figure 1: 3-dimensionnal model of a curved-roof Figure 2: A real-life photograph of an
building that will be considered throughout this exemplary building of the same structure that
document. will be discussed in this document.
Now, it can be seen from Figure 1 that the front view of this building has a parabolic shape and can be
expressed with a mathematical equation. The graphical representation of the function used to model
this part of the building is shown below in Figure 3.
y
35
30
25
20
15
10
5
x
-36 -30 -24 -18 -12 -6 6 12 18 24 30 36
-5
Figure 3: Front view of building represented as a graph.
From Figure 3, the parabolic model function of the front view of the building can be found using the
standard form of a quadratic equation, which is,
2

2. Geun Ho Lee
IB Math HL
y ax 2 bx c
The graphical model of the front view of the building intersects the x-axis at two constant points, (-
36,0) and (36,0), as the width of the building is 72 meters. Therefore, the roots of the quadratic
equation to describe this must be x 36 . Also, the height of the building is 36 meters, creating a y-
intercept at (0,36). From this, we can extrapolate that the model equation is:
y k ( x 36)( x 36) ,
where k is a constant. By substituting (0,36),
36 k ( x 36)( x 36)
36 1
k
1296 36
Therefore, the equation to model the front face of the building as shown in Figure 3 is:
1 2
y ( x 1296) (m)
36
A cuboid is a solid figure bounded by six faces, forming a convex polyhedron of parallelogram faces1.
To find a maximum volume of a cuboid that can fit in the building shown in Figure 1, the
mathematical process of optimization must be used. By optimizing the area of a rectangular face upon
the parabolic building front, the maximum volume can mathematically be found.
Figure 4: An example of a cuboid within the building structure.
Now, consider arbitrary points on the model function of the front of the building. In Figure 5, the
drawn in lines to connect these arbitrary points show the front view of Figure 4, in which the cuboid is
fit into the building.
3

3. Geun Ho Lee
IB Math HL
y
36
(-x,y) (x,y)
30
24
18
12
6
x
-36 -30 -24 -18 -12 -6 6 12 18 24 30 36
-6
Figure 5: Arbitrary points modeled and rectangle formed on the graphical representation of the front
view of the building.
From preliminary knowledge, the formula for finding the area of a rectangle is:
Arectangle (base) (height )
From Figure 5, the rectangle formed by the arbitrary points has a base of 2x and a height of y. Thus:
Arectangle 2 xy
However, the value of y is known; it is the equation of the model function of the front of the building,
1 2
y ( x 1296) . By substituting this into the area formula, the formula becomes:
36
1 2
Arectangle 2 x ( x 1296)
36
1 3
Arectangle ( x 1296 x) (m2)
18
Now, to optimize the area of the rectangle, this area function will be differentiated. The derivative
function of the area formula is the following:
dA 1
(3x 2 1296)
dx 18
dA 1 2
x 72
dx 6
dA
Solving this equation for when = 0 yields x-values of points where slope of tangent lines to the
dx
area function is zero and using first derivative test, these values can be verified as to be local
maximum or local minimum points. The process is shown below:
1 2
x 72 0
6
4

4. Geun Ho Lee
IB Math HL
x 2 432
x 12 3 (m)
First Derivative Test:
12 3 12 3
dA
dx
at x 12 3(m), area of rectangle is maximum
Now, by substituting the x-value found above into the area equation, the y-value is found to be:
1 3
Areactangle ( x 1296 x)
18
1
Areactangle (5184 3 15552 3)
18
Areactangle 576 3 (m2)
The length of the building structure is a constant 150 meters, the volume for a cuboid can be found by
multiplying the area of a reactangular face by the length. This calculation done using the maximum
area of the rectangle found above results in the maximum volume of a cuboid:
Vcuboid 150 A
Vcuboid 86400 3 (m3)
This volume is the maximum volume of a cuboid that could fit into a building structure shown in
Figure 1 with height of 36 meters. When the height of the structure is varied, the maximum volume of
the cuboid will also vary. To find how the change in height affects the change in the volume of the
cuboid, a general equation with height as a variable for the parabolic building face must be found.
Recall that the width of the building is a constant 72 meters, hence will have roots at (36,0) and (-
36,0). If the height, h, were to be varied, then the y-intercept, (0,h) will be varied. Therefore, using the
equation of the front view model equation and the x- and y-intercepts, height h can be incorporated
into area and volume equations.
y k ( x 36)( x 36)
h k (0 36)(0 36)
h
k
1296
h
y ( x 2 1296)
1296
Based on this equation, the formula for area of a rectangle for the arbitrary points on a parabola
similar to the one shown in Figure 5 can be found.
Arectangle 2 xy
h
Arectangle 2x ( x 2 1296)
1296
5

5. Geun Ho Lee
IB Math HL
h
Arectangle ( x3 1296 x) (m2)
648
By optimizing this formula, the x-value yielding maximum area of the rectangle can be found:
dA h
(3x 2 1296)
dx 648
h
(3x 2 1296) 0
648
x 2 432
x 12 3 (m)
From this, it is implied that the x-value that optimizes the area for a rectangle occurs at x 12 3 .
However, the y-value is dependent on the height of the building as shown below:
h
y ( x 2 1296)
1296
h
y (432 1296)
1296
2
y h
3
Therefore, the maximum volume of a cuboid that could fit into a building of length 150 meters, width
of 72 meters, and height of h meters can be expressed as the following:
Vcuboid 150 Areactangle
Vcuboid 150 2 xy
2
Vcuboid 150 2(12 3)( h)
3
Vcuboid 2400h 3 (m3)
This relationship between the maximum volume of the cuboid and the height of the building structure
is verified through multiple calculations as shown in Table 1 and Figure 6.
Height of x-value for y-value for max Area of rectangle max volume of
building (m) maximum volume (m) (m2) cuboid (m3)
volume (m)
36 12 3 24 997.66127 149649.19
37 12 3 2 1025.3741 153806.11
24
3
38 12 3 1 1053.0869 157963.03
25
3
39 12 3 26 1080.7997 162119.96
40 12 3 2 1108.5125 166276.88
26
3
41 12 3 1 1136.2253 170433.8
27
3
42 12 3 28 1163.9381 174590.72
6

6. Geun Ho Lee
IB Math HL
43 12 3 2 1191.651 178747.64
28
3
44 12 3 1 1219.3638 182904.57
29
3
45 12 3 30 1247.0766 187061.49
46 12 3 2 1274.7894 191218.41
30
3
47 12 3 1 1302.5022 195375.33
31
3
48 12 3 32 1330.215 199532.25
49 12 3 2 1357.9278 203689.17
32
3
50 12 3 1 1385.6406 207846.1
33
3
51 12 3 34 1413.3535 212003.02
52 12 3 2 1441.0663 216159.94
34
3
53 12 3 1 1468.7791 220316.86
35
3
54 12 3 36 1496.4919 224473.78
Table 1: This table provides the values used to calculate the maximum volume of a cuboid for
different values for the height of the curved roof structure the cuboid is placed in. These can be used
to show the effects of the change in height of the building structure on the volume of the cuboid.
Figure 6: Graph of height of a building structure vs. maximum volume of a cuboid.
7

7. Geun Ho Lee
IB Math HL
The graph in Figure 6 shows that the maximum volume of the cuboid linearly increases when the
height of the building is increased. The slope, 4157m3 (= 2400 3 ), is congruent with the
algebraically found value, thus confirms the relationship.
The wasted space in the building refers to the space of the building not occupied by the cuboid floors.
To find the volume of the wasted space, the maximum volume of the cuboid has to be subtracted from
the volume of the building structure. This is shown below:
Vwasted Vtotal Vcuboid ,
where Vwasted is the volume of wasted space, Vtotal is the total volume of the building structure.
The total volume of the building can be calculated by taking the definite integral of the parabolic face
and multiplying by the length of the building. Mathematically presented, this would be as following:
Vtotal Aparabola (length)
The process of finding area of the parabolic face is shown below:
36
Aparabola y dx
36
36 h
Aparabola ( x 2 1296) dx
36 1296
36
h 1 3
Aparabola x 1296 x
1296 3 36
h 1
Aparabola 363 ( 36)3 1296 36 ( 36)
1296 3
h
Aparabola ( 62208)
1296
Aparabola 48h (m2)
Thus, the total volume of the structure is,
Vtotal Aparabola (length)
Vtotal (48h) (150)
Vtotal 7200h (m3)
Then, the formula for finding the volume of wasted space is,
Vwasted Vtotal Vcuboid
Vwasted 7200h 2400h 3 2400h(3 3) (m3)
The ratio of wasted volume to the volume of the cuboid for all heights h is as the following:
Vwasted 7200h 2400h 3
Vcuboid 2400h 3
Vwasted
3 1
Vcuboid
This relationship is clearly shown in Table 2.
8

8. Geun Ho Lee
IB Math HL
Height V total V cuboid V wasted V wasted / V
cuboid
36 259200 86400 3 109550.8 0.732051
37 266400 88800 3 112593.9 0.732051
38 273600 91200 3 115637 0.732051
39 280800 93600 3 118680 0.732051
40 288000 96000 3 121723.1 0.732051
41 295200 98400 3 124766.2 0.732051
42 302400 100800 3 127809.3 0.732051
43 309600 103200 3 130852.4 0.732051
44 316800 105600 3 133895.4 0.732051
45 324000 108000 3 136938.5 0.732051
46 331200 110400 3 139981.6 0.732051
47 338400 112800 3 143024.7 0.732051
48 345600 115200 3 146067.7 0.732051
49 352800 117600 3 149110.8 0.732051
50 360000 120000 3 152153.9 0.732051
51 367200 122400 3 155197 0.732051
52 374400 124800 3 158240.1 0.732051
53 381600 127200 3 161283.1 0.732051
54 388800 129600 3 164326.2 0.732051
Table 2: This table shows the relationship that was found above by using multiple calculations of
specific heights. It is important to note that the ratios of volume of wasted space to maximum volume
of cuboid are always constant to be 0.732051, which is about 3 1 , the algebraically derived value.
The cuboid that fits in the curved roof structure can be divided into a number of floor often seen in
office buildings as illustrated in Figure 7 and 8.
9

9. Geun Ho Lee
IB Math HL
y
35
30
25
20
15
10
5
x
-36 -30 -24 -18 -12 -6 6 12 18 24 30 36
-5
Figure 7: Front view of curved roof structure and a cuboid fitting inside. The solid lines indicate the
cuboid office block and the dotted lines indicate the floors.
Figure 8: This is a 3-dimenssional representation of stacked cuboids under the building structure, with
the structure not shown. The lines indicate the various floors that can be placed like in an office
building.
To find the maximum floor area of such an office building, the following formula is implemented:
Afloor N Aface
where Afloor is the maximum floor area, N is the number of floors that can fit in the cuboid, and Aface is
the area of the top face of each floor.
Now, recall that one of the specifications of a functional building was that the minimum height for
10

10. Geun Ho Lee
IB Math HL
each floor must be 2.5 meters. Thus, the number of floors and ultimately, the maximum floor area are
limited by the height of the cuboid. However, it was found from above that the height of the cuboid is
dependent on the height of the curved roof structure and the relationship is:
2
y h
3
Hence, the total number of floors for a height h is,
2
h
N 3
2.5
4
N h
15
As the number of floors cannot be a non-integer value, the value of N is rounded down to the nearest
whole number. Substituting this back into the floor area equation,
Afloor N Aface
4
Afloor h 2( x)(length)
15
4
Afloor h 2(12 3)(150)
15
Afloor 960h 3 (m2)
In this floor area equation, it is very important to note that N is an integer.
This relationship is clearly shown in Table 3 below.
Height Number of floors Area of cuuboid face Floor area
36 10 3600 3 36000 3
37 10 3600 3 36000 3
38 10 3600 3 36000 3
39 10 3600 3 36000 3
40 11 3600 3 39600 3
41 11 3600 3 39600 3
42 11 3600 3 39600 3
43 11 3600 3 39600 3
44 12 3600 3 43200 3
45 12 3600 3 43200 3
46 12 3600 3 43200 3
47 13 3600 3 46800 3
48 13 3600 3 46800 3
49 13 3600 3 46800 3
50 13 3600 3 46800 3
11

11. Geun Ho Lee
IB Math HL
51 14 3600 3 50400 3
52 14 3600 3 50400 3
53 14 3600 3 50400 3
54 14 3600 3 50400 3
Table 3: This table presents the maximum floor area for different heights of the building structure.
To maximize floor area even further, the floors do not have to be part of one cuboid, but rather fit
within the confines of the curved roof sturucture as show in Figure 9.
Figure 9: maximizing office space by having the floors (the lines on the parabolic face) not confined
to shape of one cuboid.
The calculations for the method shown in Figure 9 can be accomplished by finding a rectangular
prism of height of 2.5 meters that fits inside the curved roof. The surface area of this block is recorded.
Then, another rectangular prism of height 2.5 meters on top of the first one is found and recorded.
Mathematically, this can be accomplished by finding the x-value for the point (x,2.5n) that lies on the
equation of the curve, where n is the floor number. This is illustrated in Figure 10. This will
correspond with half the width of that particular floor.
12

12. Geun Ho Lee
IB Math HL
y
36
(x4,10)
30
(x3,7.5)
24
(x2,5)
18
(-x1,2.5) 12 (x1,2.5)
6
x
-36 -30 -24 -18 -12 -6 6 12 18 24 30 36
-6
Figure 10: Example of maximizing area by finding the x-value per 2.5 increments of y-values. As
indicated in the graph, the width of cuboid is 2xn, where n is the floor number.
A mathematical notation to symbolize this is the following:
N
Aoffice ( width)(length) ,
n 1
where N is the number of floors within the curved structure, which is related to the height of the
building. The length remains a constant 150 meters for this particular building. The width of the floor
is dependent on the height of the structure, as it is derived from the curve equation for every floor.
Finding the width, which is 2x, the general equation of the curve is,
h
y ( x 2 1296)
1296
h 2
y x h
1296
1296(h y)
x2
h
1296( y h)
x (m)  x 0
h
As the y-values are increments of 2.5 meters, it can be stated that y 2.5n , where n is the floor
number. Therefore,
1296(2.5n h)
x (m)
h
This is the half the width of a floor. By substituting 2x as the width of a floor into the office area
equation above, the equation becomes,
N
Aoffice ( width)(length)
n 1
13

13. Geun Ho Lee
IB Math HL
4
h
15
1296(2.5n h)
Aoffice (2 )(150)
n 1 h
4
h
15
1296(2.5n h) 2
Aoffice 300 (m )
n 1 h
By using this method, the floor area has increased significantly as seen in the following table.
Height Stacking floor area cuboid max floor area increase in floor area
36 83727.93 59859.68 23868.26
37 84530.57 61522.44 23008.13
38 85278.89 63185.21 22093.68
39 85978.59 64847.98 21130.6
40 92671.92 66510.75 26161.17
41 93448.18 68173.52 25274.66
42 94177.18 69836.29 24340.89
43 94863.39 71499.06 23364.34
44 101602.7 73161.83 28440.89
45 102357.9 74824.59 27533.28
46 103071.2 76487.36 26583.88
47 109745.2 78150.13 31595.02
48 110523.8 79812.9 30710.88
49 111261.7 81475.67 29785.98
50 111962.1 83138.44 28823.68
51 118677.3 84801.21 33876.12
52 119437.4 86463.98 32973.45
53 120160.9 88126.75 32034.16
54 120850.5 89789.51 31061.01
Table 4: This table indicates a significant increase in the maximum floor area by not limiting the
floors to within the shape of one cuboid.
The volume ratio of office space has also significantly decreased as a result of this new flooring
method. The volume of the office block was calculated by multiplying the area of the floors by 2.5,
the height of each floor blocks.
Height V office V total V wasted V wasted/V office
36 209319.8 259200 49880.16 0.238296
37 211326.4 266400 55073.57 0.260609
38 213197.2 273600 60402.78 0.283319
39 214946.5 280800 65853.54 0.306372
40 231679.8 288000 56320.21 0.243095
41 233620.4 295200 61579.55 0.263588
42 235443 302400 66957.05 0.284388
43 237158.5 309600 72441.51 0.305456
44 254006.8 316800 62793.2 0.247211
45 255894.7 324000 68105.32 0.266146
46 257678.1 331200 73521.89 0.285325
47 274362.9 338400 64037.11 0.233403
48 276309.4 345600 69290.55 0.250772
49 278154.1 352800 74645.86 0.268362
14

14. Geun Ho Lee
IB Math HL
50 279905.3 360000 80094.71 0.286149
51 296693.3 367200 70506.68 0.237642
52 298593.6 374400 75806.44 0.253878
53 300402.3 381600 81197.74 0.270297
54 302126.3 388800 86673.69 0.286879
Table 5: This table demonstrates the new volumes and new ratio of office blocks instead of having
them limited by a shape of one cuboid. As it can be seen, the ratio is significantly less than the values
in Table 2.
Hence, not limiting the floors to a single cuboid, the efficiency in utilizing space of the building
structure notably increased, although not at a constant ratio because the number of floors is a discrete
value, which causes volumes to fluctuate depending on height.
These aspects of the curved roof structure are not limited to the specific dimensions mentioned at the
beginning. For instance, consider a similar building structure of different dimensions; width of 150
meters and length of 72 meters as illustrated in Figure 11. This new building structure follows the
same specifications as mentioned at the beginning.
Figure 11: A similar building to the initially considered building structure. This new building structure
is used to investigate the impact of a different building on the general trends of the values observed
above.
Using the same procedure, a general parabolic curve equation can be set up of the front view of the
structure. The width of 150 meters indicate that the roots of this quadratic equation are (75,0) and (-
75,0). Thus, the equation is,
y k ( x 75)( x 75)
h k (0 75)(0 75)
h
k
5625
15

15. Geun Ho Lee
IB Math HL
h
y ( x 75)( x 75)
5625
The maximum volume of a cuboid that fits in this building can be found by optimization of the area of
a rectangle.
Arectangle 2 xy
2h
Arectangle ( x3 5625 x)
5625
dA 2h
(3x 2 5625)
dx 5625
x2 1875
x 25 3 (m)
From this, y-value of the rectangle can be deduced:
h
y ( x 2 5625)
5625
h
y (1875 5625)
5625
2
y h
3
This relationship between the y-value of the rectangle and the height h of the building is exactly the
same as the initially considered building structure. For the volume, the same formula is used to find
the general relationship.
Vcuboid (length) Arectangle
Vcuboid 72 2 xy
2
Vcuboid 72 2(25 3)( h)
3
Vcuboid 2400h 3 (m3)
This relationship between the volume of the cuboid and the height of the building is the same as the
one for the initially considered building structure. This leads to a conclusion that bases of the same
dimension will produce volumes of equal proportions. Extending on this to other aspects that were
investigated such as the ratio of volume of wasted space to the volume of cuboid, more similarities
can be seen. The total volume is,
Vtotal Aparabola (length)
Area of parabola is as shown in page 7,
75
Aparabola ydx
75
75 h
Aparabola ( x 2 5625) dx
75 5625
Aparabola 100h (m2)
Vtotal 7200h (m3)
Thus, finding the ratio of volume of wasted space to the volume of the cuboid,
16

16. Geun Ho Lee
IB Math HL
Vwasted Vtotal Vcuboid
Vwasted Vtotal Vcuboid
Vcuboid Vcuboid
Vwasted 7200h 2400h 3
Vcuboid 2400h 3
Vwasted
3 1
Vcuboid
Again, the ratio of volume of wasted space to the volume of cuboid is exactly the same. Some values
of height were used to calculate and verify this relationship as shown in Table 6.
Height V total V cuboid V wasted V wasted/V
cuboid
75 540000 311769.15 228230.85 0.7320508
78 561600 324239.91 237360.09 0.7320508
81 583200 336710.68 246489.32 0.7320508
84 604800 349181.44 255618.56 0.7320508
87 626400 361652.21 264747.79 0.7320508
90 648000 374122.97 273877.03 0.7320508
93 669600 386593.74 283006.26 0.7320508
96 691200 399064.51 292135.49 0.7320508
99 712800 411535.27 301264.73 0.7320508
102 734400 424006.04 310393.96 0.7320508
105 756000 436476.8 319523.2 0.7320508
108 777600 448947.57 328652.43 0.7320508
111 799200 461418.34 337781.66 0.7320508
Table 6: This table shows that the new building follows the same wasted space to cuboid volume ratio.
Note that the height of this building is larger than the previous one, because following the
specifications listed at the beginning, the height of this building is between 75 and 112.5 meters. Also
note that 0.7320508 is about 3 1 , which is the same as the ratio value in Table 2.
To maximize floor area for this new building, the same formula used in page 9 will be implemented:
Afloor N Aface
where Afloor is the maximum floor area, N is the number of floors that can fit in the cuboid, and Aface is
the area of the top face of each floor.
y
N
2.5
2
h
N 3
2.5
4
N h
15
As the number of floors cannot be a non-integer value, the value of N is rounded down to the nearest
whole number. Substituting this back into the floor area equation,
Afloor N Aface
17

17. Geun Ho Lee
IB Math HL
4
Afloor h 2( x)(length)
15
4
Afloor h 2(25 3)(72)
15
Afloor 960h 3 (m2)
This is again the same maximum floor area equation as above. From these observations, it is plausible
to conclude that the placement of the façade on a building does not affect the maximum floor area,
volume, and ratio of volume of wasted space to volume of cuboid.
18