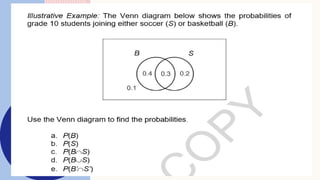
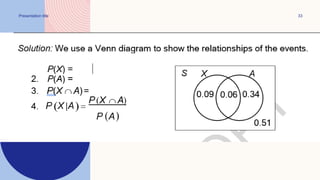
The document covers various topics in probability and counting principles, including the probability of mutually exclusive events and odds. It presents examples and exercises related to selecting outcomes from different scenarios, such as letter combinations and arrangements of students. Additionally, it discusses the fundamental counting principle and various applications of permutations and combinations.

1. GE 2
PROBABILITY
(MUTUALLY
EXCLUSIVE EVENTS)

2. 2
PRAYER

3. Presentation title 3

4. Presentation title 4

5. Presentation title 5

6. Presentation title 6

7. Presentation title 7

8. Presentation title 8

9. Presentation title 9

10. Presentation title 10

11. Presentation title 11

12. Presentation title 12

13. Presentation title 13

14. 14
SEATWORK
A letter is selected at random from each of the
words “POOR” and “ELITE”.
1. Show the sample space using a tree diagram.
2. Find the probability that the two letters selected
are
a. both vowels
b. both consonants
c. a vowel and a consonant

15. 15
PROBABILITY OF ODDS
The odds of an event occurring is the ratio of the number
of favorable outcomes to the number of unfavorable
outcomes. In symbol:

16. Presentation title 16
EXAMPLE
1. A box contains 5 blue marbles, 4 red marbles and 2 white marbles. Find
the odds of choosing:
a. A blue marbles b. a red marbles c. a white marbles
2. A fair six sided die is rolled. Find the
b. The odds that the number is even.
c. The probability that the number is
i. even
ii. Multiple of 3
iii. Multiple of 5
iv. Even and a multiple of 3
v. an even or a multiple of 5

17. Presentation title 17

18. Presentation title 18

19. Presentation title 19

20. Presentation title 20

21. Presentation title 21

22. Presentation title 22

23. Presentation title 23

24. Presentation title 24

25. Presentation title 25

26. Presentation title 26

27. Presentation title 27

28. Presentation title 28

29. 29
MODULE 14-15: PROBABILITY
Asynchronous Class Today
Video Lesson posted on
Gclass
ACTIVITY
https://bit.ly/2023_GE2_M14_
15
https://bit.ly/
2023_GE2_M14_15

30. Presentation title 30
UNION AND
INTERSECTION
1. How many students are in the
senior class?
2. How many students participate in
athletics?
3. If a student is randomly
chosen, what is the
probability that the student
participates in athletics or
drama?
4. If a student is randomly
chosen, what is the
probability that the student
participates only in drama

31. Presentation title 31

32. Presentation title 32
0.16
0.59 0.09
0.16
M R
1. )
2.
3.
4.
5. )

33. Presentation title 33

34. FUNDAMENTAL
COUNTING PRINCIPLE
SAMPLE
SPACE- the set
of all possible
outcome.

35. 35

36. 36
What is the
possible
outcome
when we
toss a
coin?

37. 37
What is the
possible
outcome
when we
roll a die?

38. 38
What is the
possible
outcome
when two-
sided dice
are rolled?

39. A family has 4 children. Draw a tree diagram to show the possible genders of the
children.

52. Choosing 5 questions to answer out
of 10 questions in a test

53. LOTTO COMBINATION

55. GRADED RECITATION

56. QUESTION
A special plate number is made up of three
letters of the English alphabet followed by two-
digit numbers. How many plate numbers are
possible if letters and digits can be repeated in
the same plate number?

57. QUESTION
A group of 15 students must elect a president, a
vice-president, a treasurer and a secretary. How
many ways can this be done?

58. QUESTION
How many distinct permutations can be made
from the letters of the word COMMOTION?

59. QUESTION
•Carla is assigned to arrange 4 boys and 4 girls to sit
at a round table. If 2 particular girls decided to sit
together, how many possible arrangements are
there?

60. QUESTION
•Suppose you are a customer and asked to
get 8 different food items in a buffet. Then,
you computed 70 possible ways as a
result, which of the following did you do?

61. QUESTION
•How may combinations can be made from H,
O, P, E if the letters are taken two at a time?

62. QUESTION
•A committee of 4 people is to be formed from a
group of 10 students. In how many ways can
the committee be formed?

63. QUESTION
•Mr. Dela Cruz needs to select a team of 9 for his
basketball team. There is a total of 15 available
players. Assuming that all of them can play any
position, how many different teams are possible?

64. QUESTION
•Suppose 7 female and 6 male contestants have
successfully passed the preliminary round of a
competition. If there are only 5 slots for the final
round of the competition, in how many ways can the
3 females and 2 males be selected?

65. QUESTION
John Lloyd is attempting to unlock his locker but has
forgotten his locker combination. The lock uses three
numbers and includes only the numbers 1 to 9. The
digits cannot be repeated in the combination. He
wanted to know the number of possible locker
combinations he needs to form. He solved the
problem using three different solutions.

66. QUESTION
John Lloyd is attempting to unlock his locker but has
forgotten his locker combination. The lock uses three
numbers and includes only the numbers 1 to 9. The
digits cannot be repeated in the combination. He
wanted to know the number of possible locker
combinations he needs to form. He solved the
problem using three different solutions.