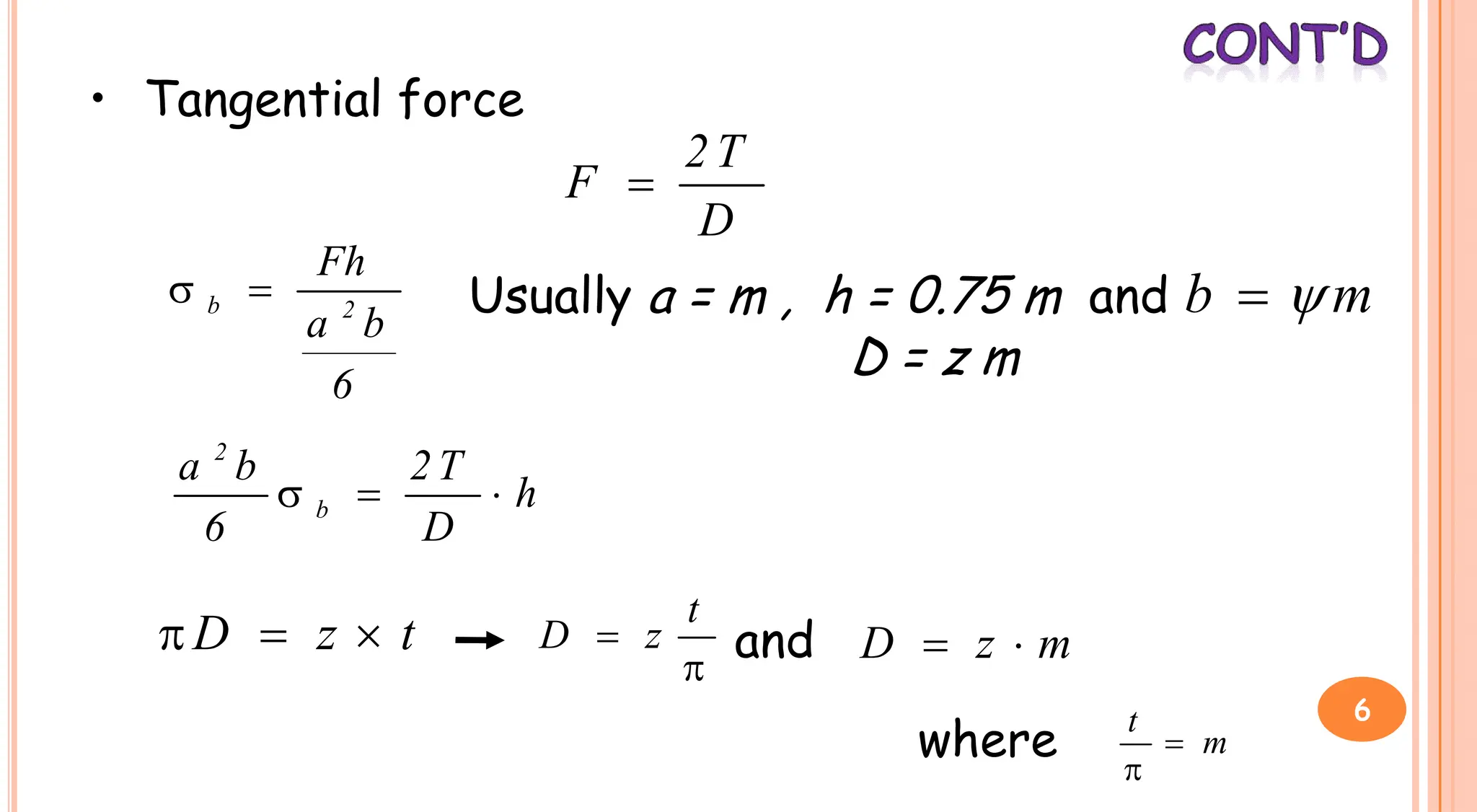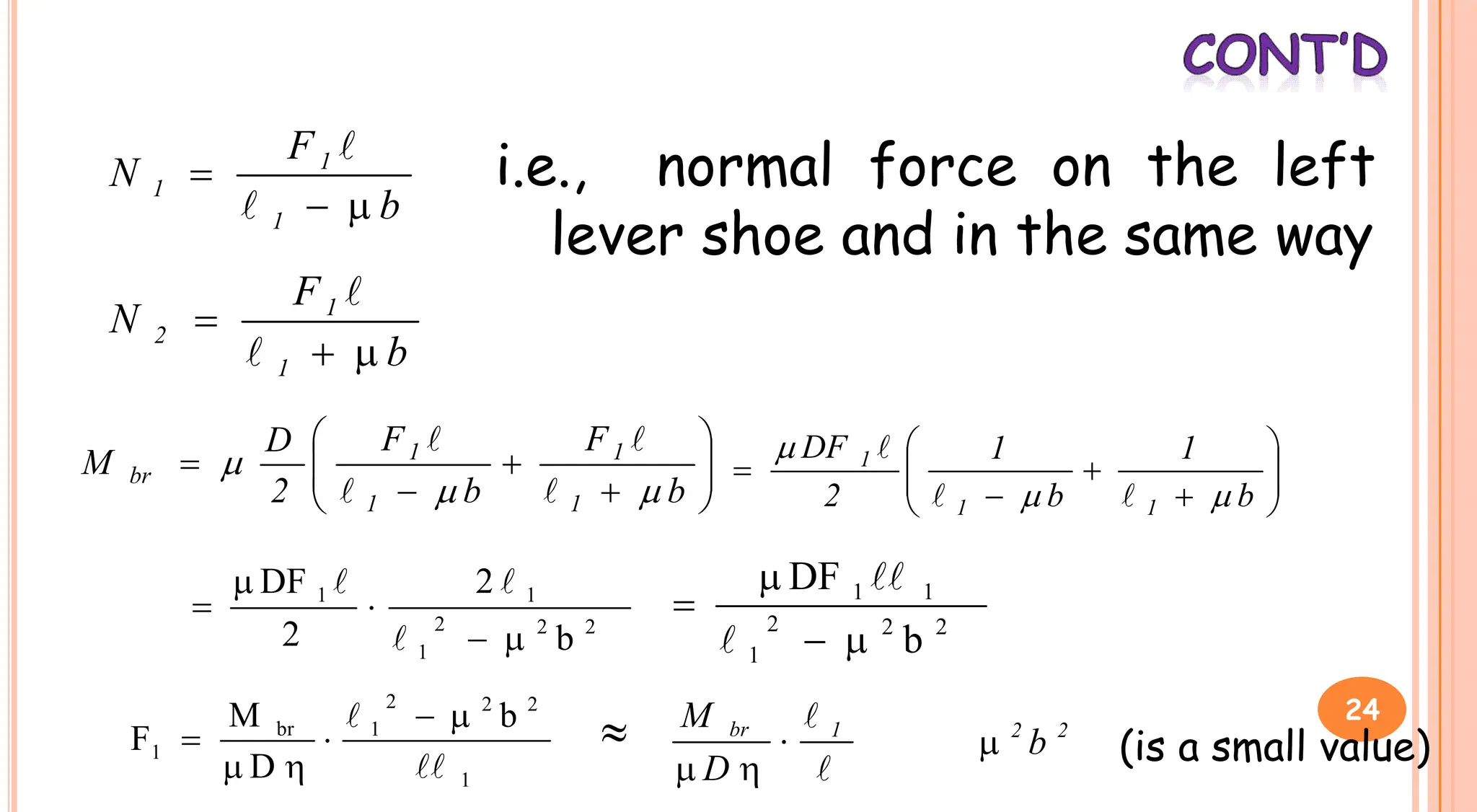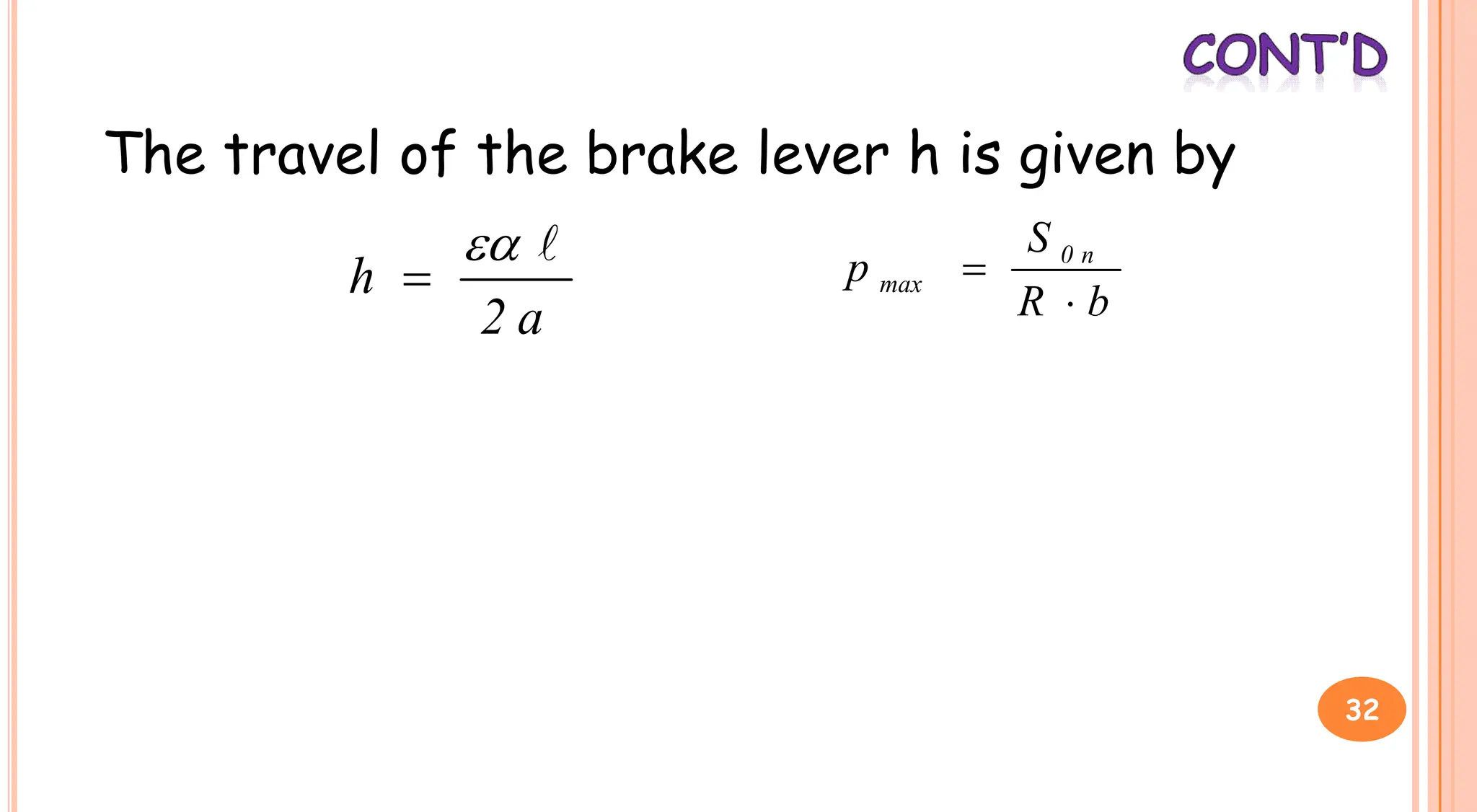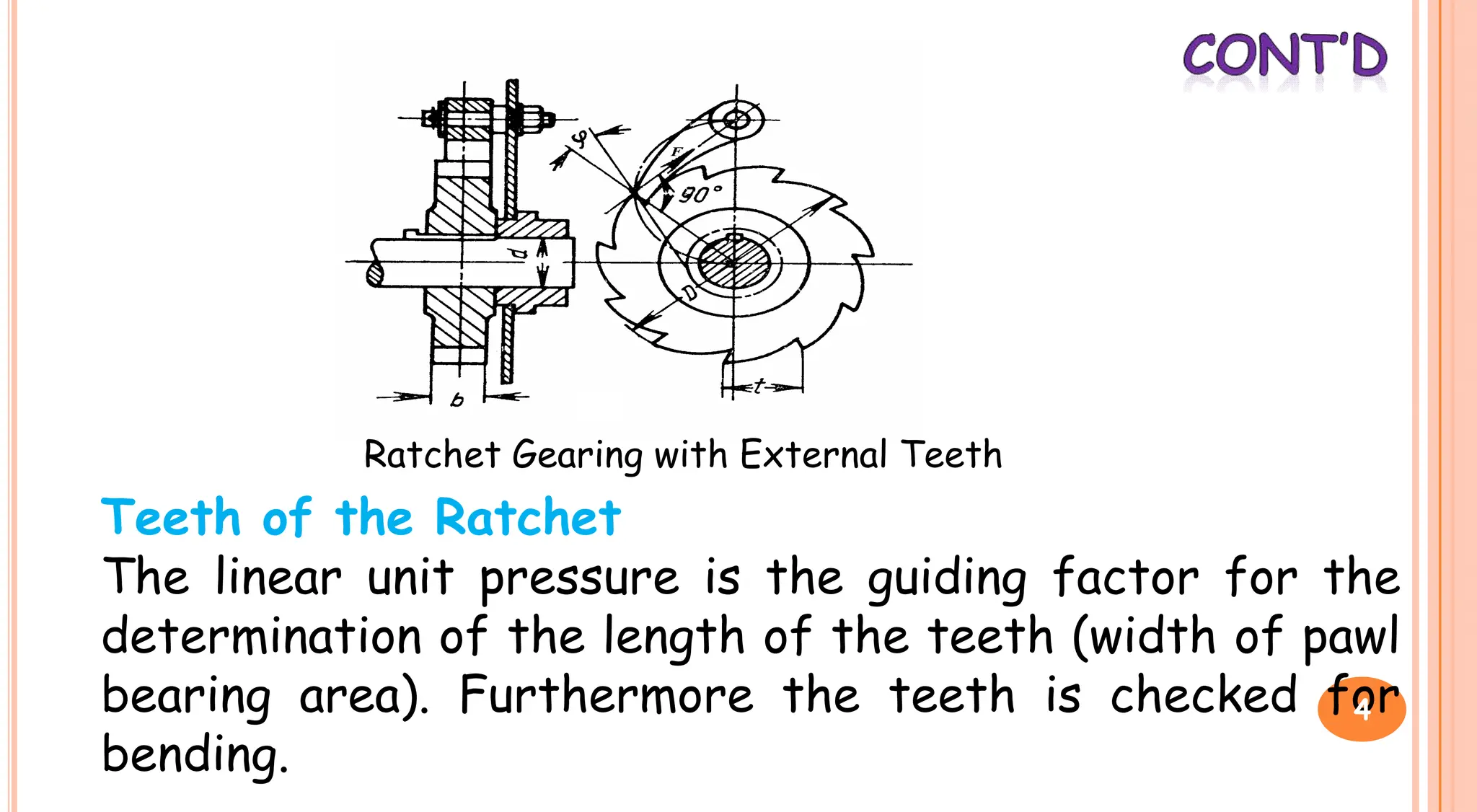
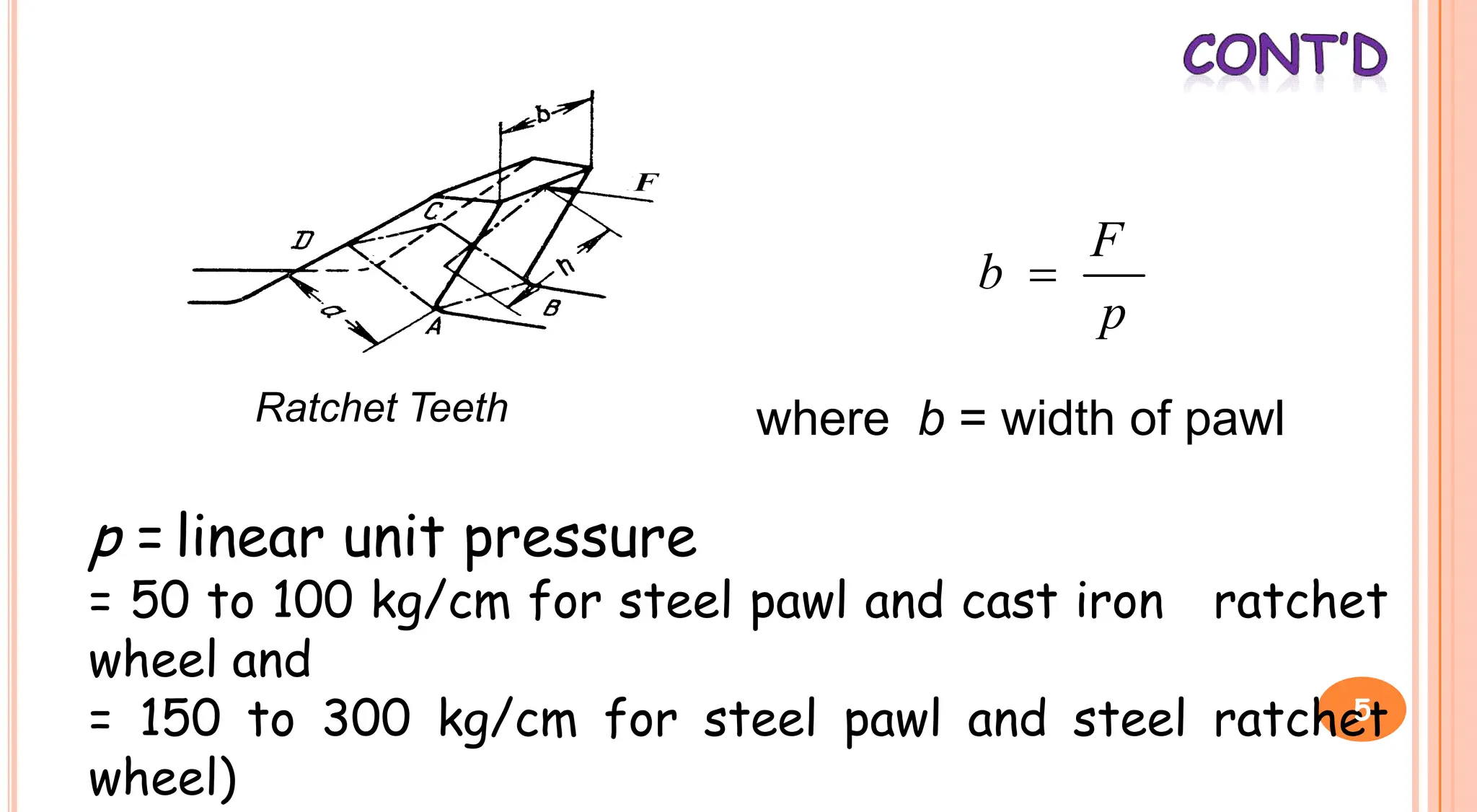
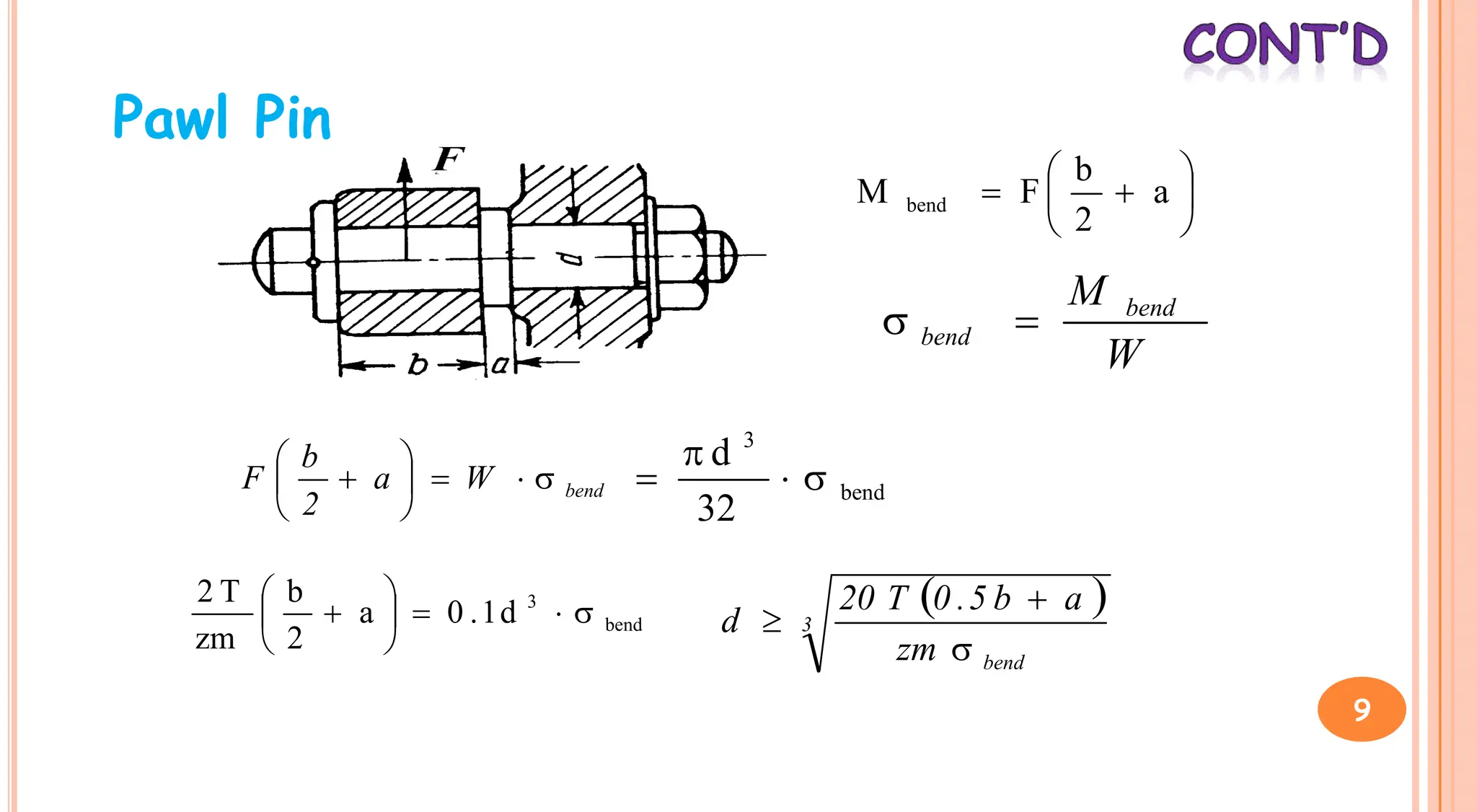
1. Arresting gear is used to hold loads being lifted without interfering with hoisting but preventing downward motion from gravity. Common arresting mechanisms include ratchet gearing and friction arresters. 2. Ratchet gearing uses a ratchet gear and pawl such that the ratchet turns freely during lifting but the pawl prevents downward motion. The width of the pawl bearing area is designed to withstand bending stresses. 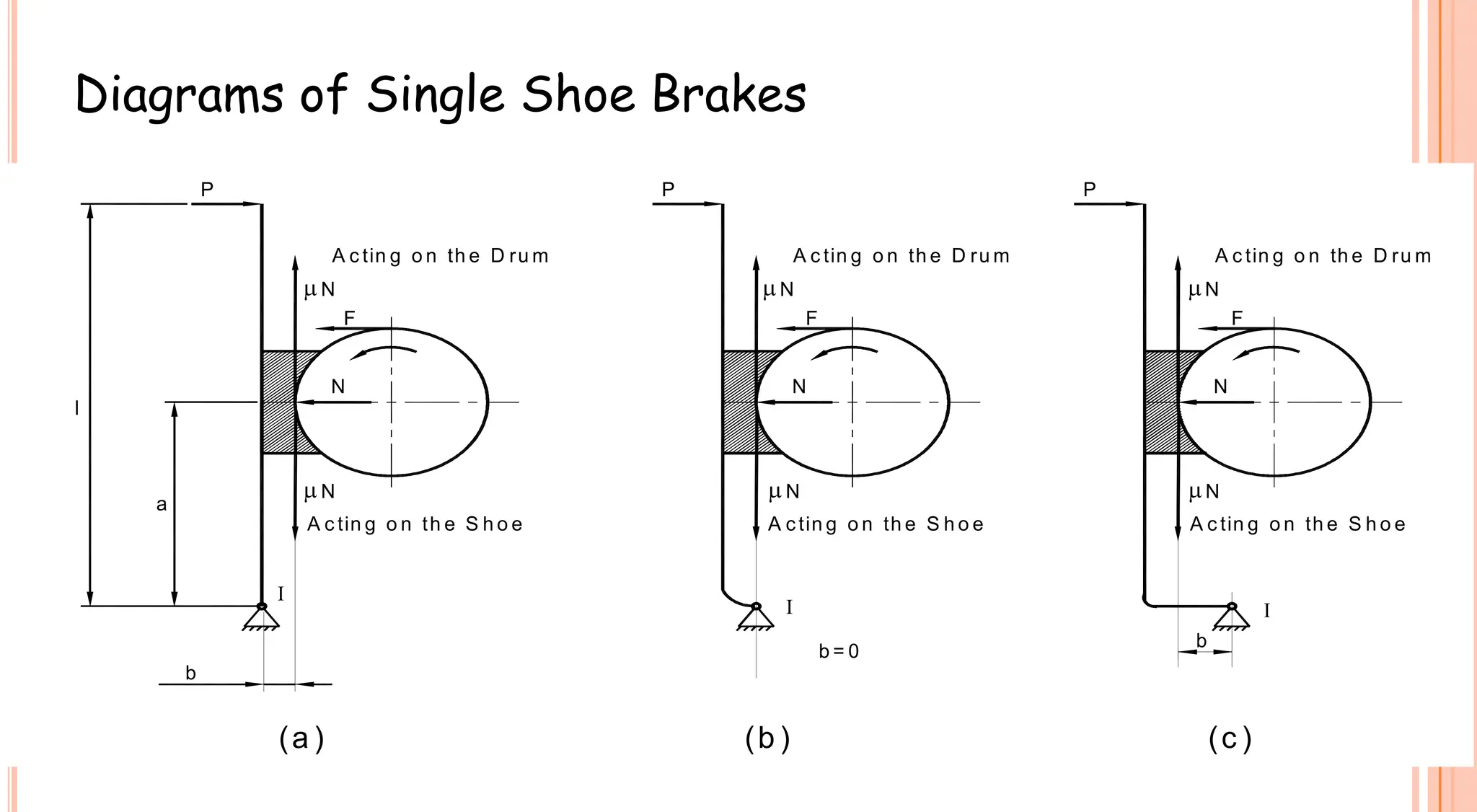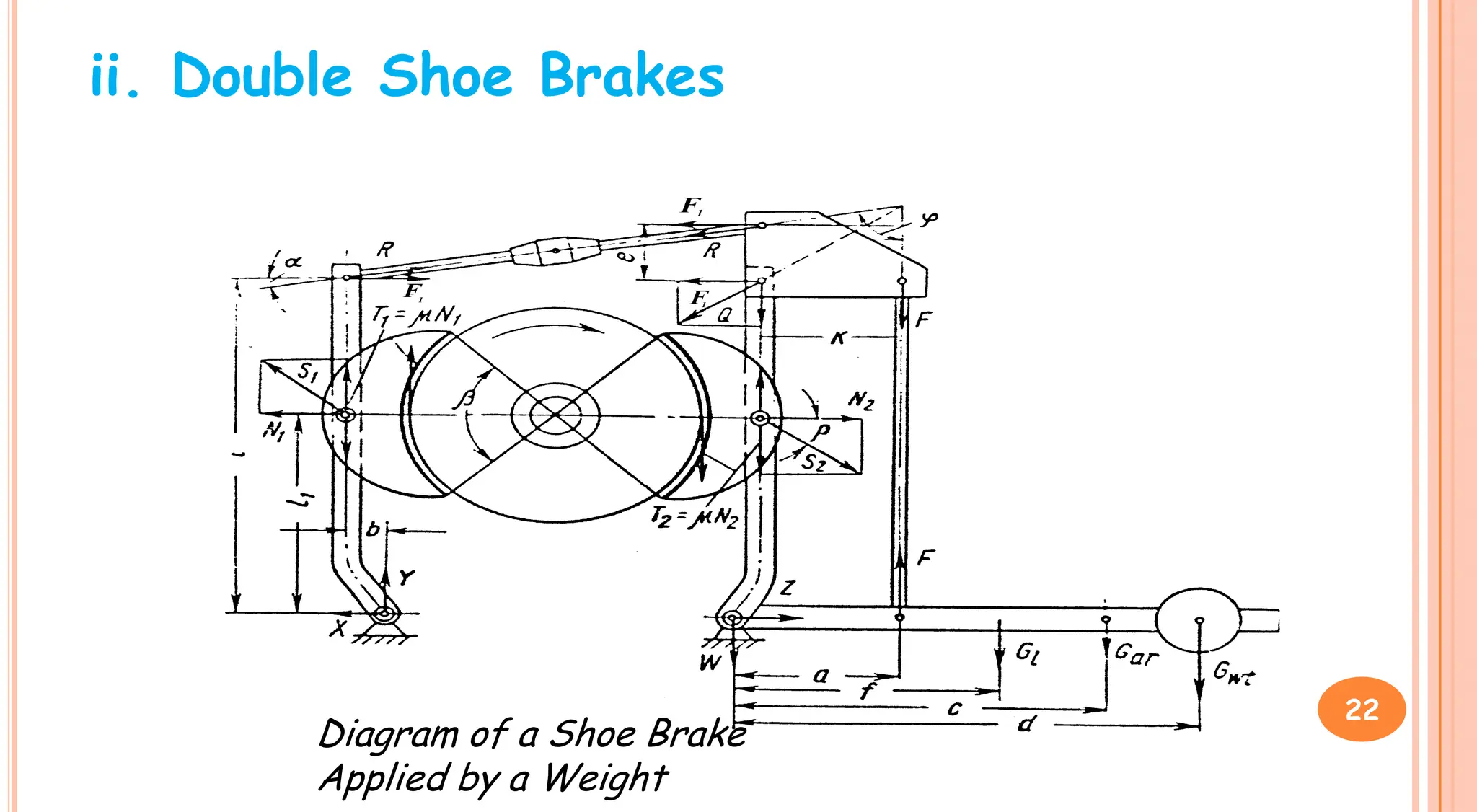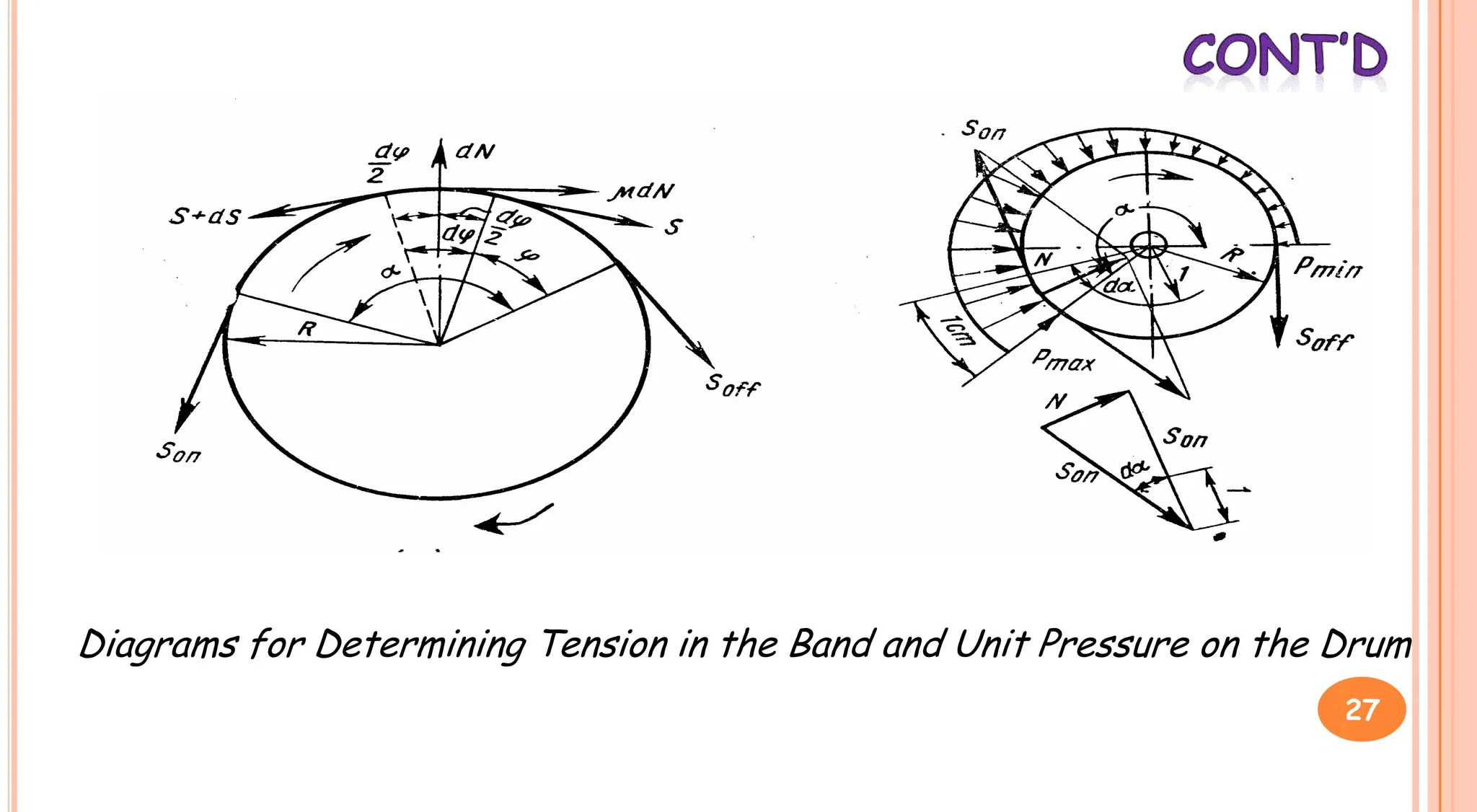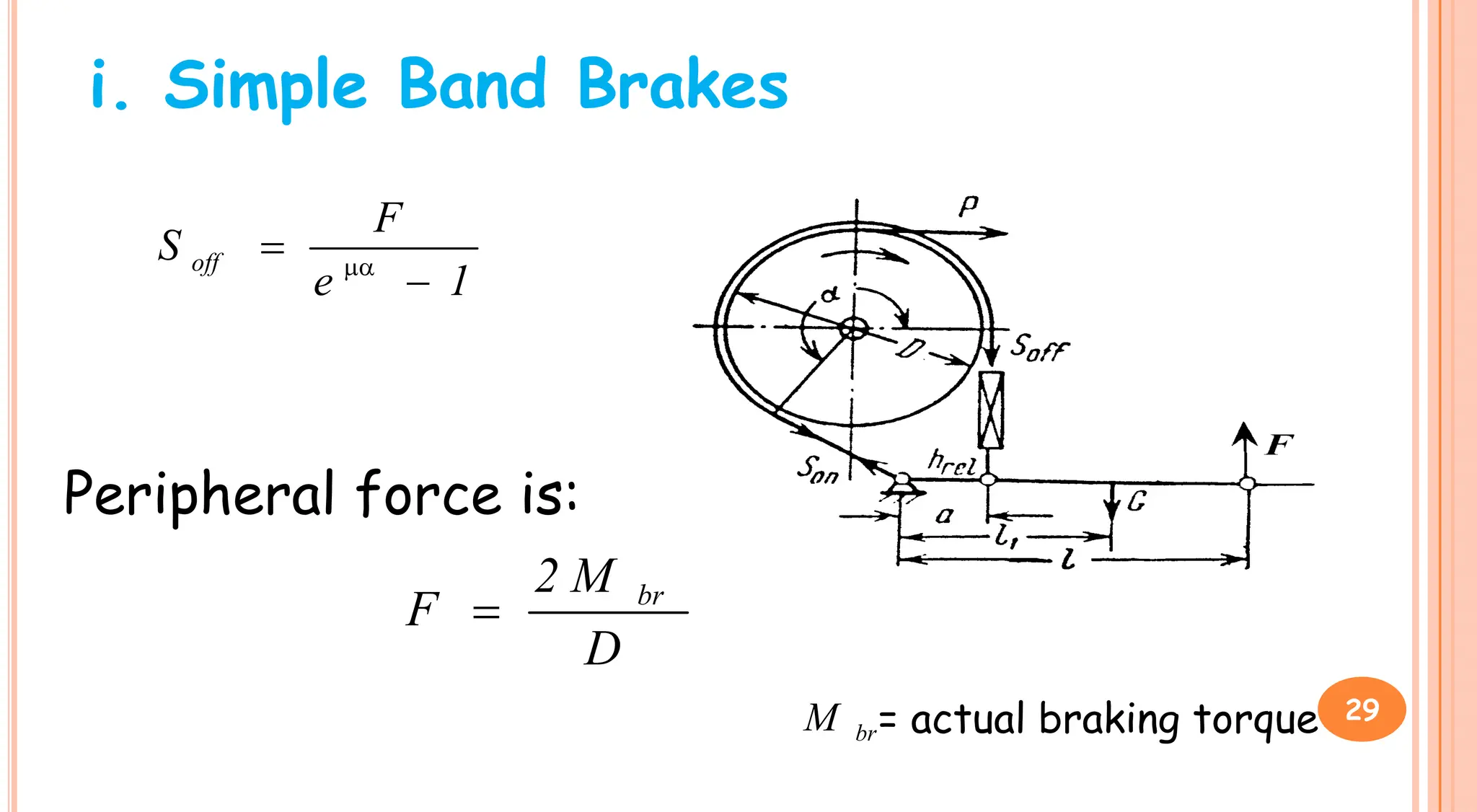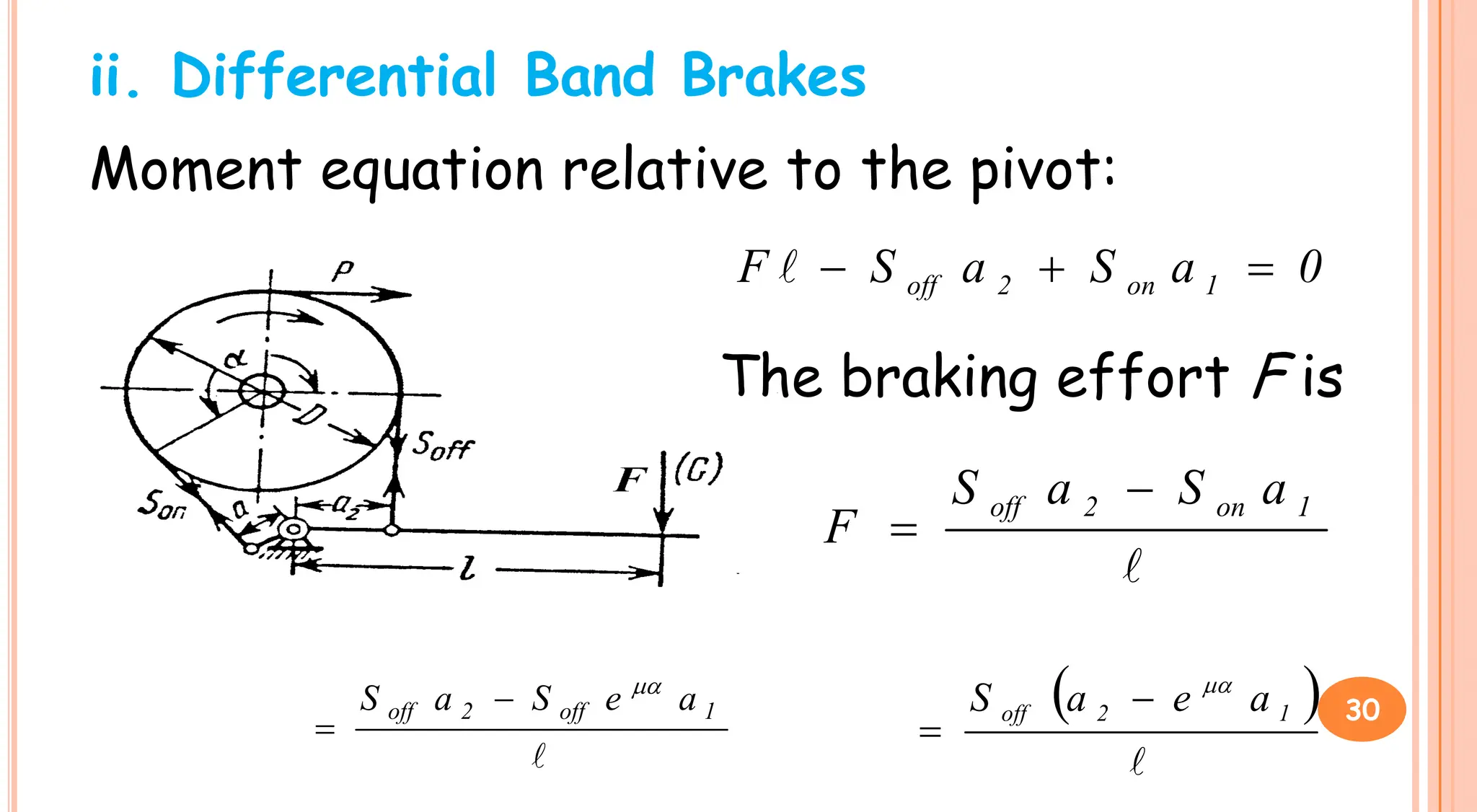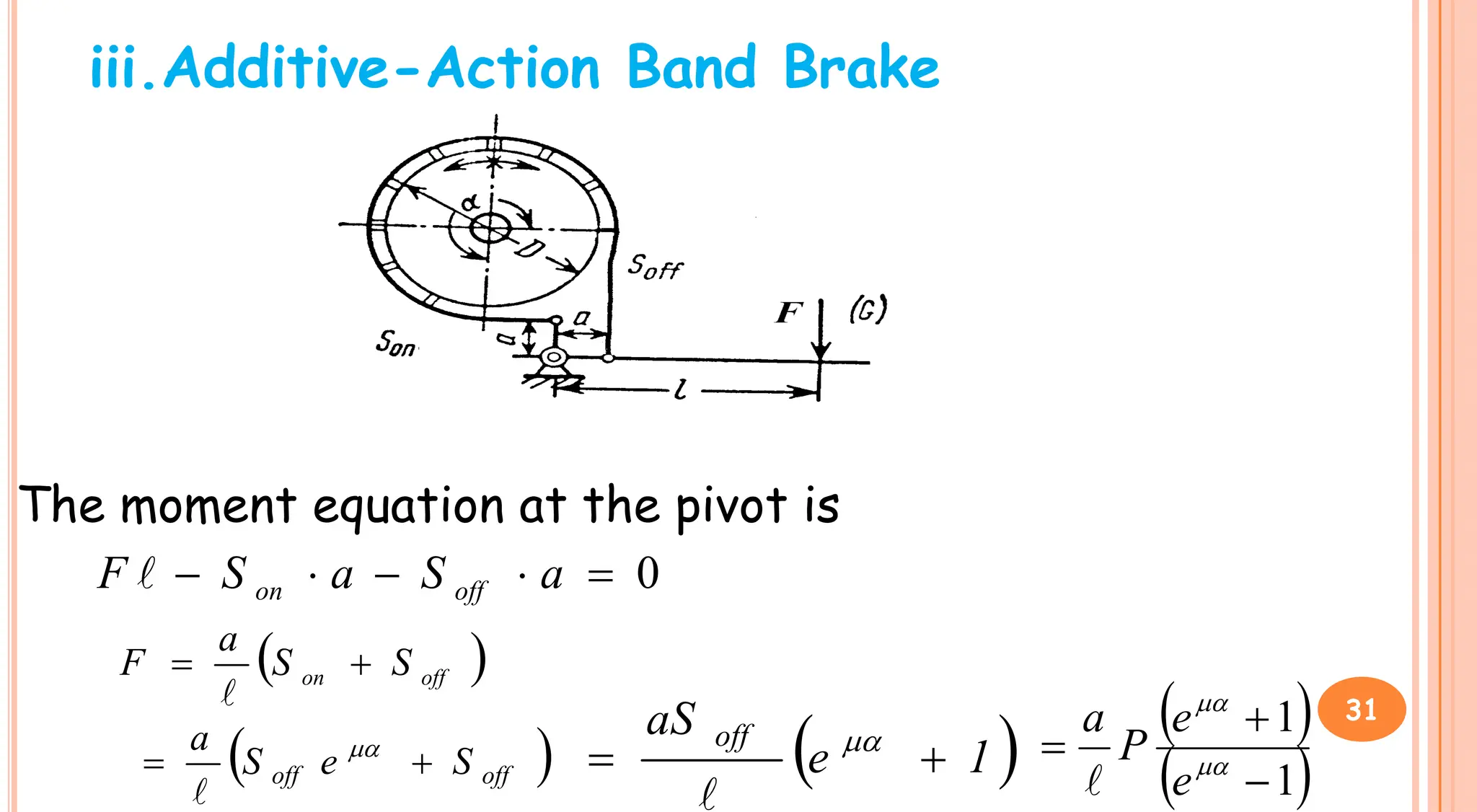3. Brakes are used to control lowering speed and hold suspended loads stationary. Common brake types include shoe brakes and band brakes, which use friction between a shoe/band and wheel to produce a braking torque opposing motion.

1. 1

2. • Arresting gear is used to hold the load being
lifted without interfering in the hoisting
process but preventing the load from coming
down due to gravity.
• Brakes are employed for controlling the speed
of the load lowering and holding the
suspended load at rest.
2

3. There are a number of arresting mechanisms used in
hoisting machineries.
i. Ratchet gearing
Consists of ratchet gear and pawl. The teeth in the
ratchet are so arranged that the ratchet runs free
when the load is being raised but prevents the load
A. Arresting gear
ratchet are so arranged that the ratchet runs free
when the load is being raised but prevents the load
from coming down because of its own weight.
a b
3

4. Ratchet Gearing with External Teeth
Teeth of the Ratchet
The linear unit pressure is the guiding factor for the
determination of the length of the teeth (width of pawl
bearing area). Furthermore the teeth is checked for
bending.
4

5. Ratchet Teeth
p
F
b 
where b = width of pawl
Ratchet Teeth where b = width of pawl
p = linear unit pressure
= 50 to 100 kg/cm for steel pawl and cast iron ratchet
wheel and
= 150 to 300 kg/cm for steel pawl and steel ratchet
wheel)
5

6. • Tangential force
D
T
2
F 
6
b
a
Fh
2
b 
 Usually a = m , h = 0.75 m and m
b 

D = z m
6
h
D
T
2
6
b
a
b
2



t
z
D 




t
z
D m
z
D 

m
t


and
where
6

7. Material of Ratchets
0.33 or 0.55 % C cast steel
1. 5 - 4
m
b


1. 5 - 4
0.3 % C steel or 0.45 % C with additive
1 - 2
7

8. Checking for Eccentricity of Pawl
A
F
W
M bend


 Where e
F
M bend 

6
x
b
W
2


all
bx
F
bx
Fe

 

 2
6








x
e
bx
F 6
1 8

9. W
M bend
bend 

Pawl Pin







 a
2
b
F
M bend
bend
W
a
2
b
F 








 bend
3
32
d




bend
3
d
1
.
0
a
2
b
zm
T
2









  
3
bend
zm
a
b
5
.
0
T
20
d



9

10. • The pin is subjected to impact loading, thus we take
reduced safe bending stress.
= 300 to 500 kgf/cm2.
• The best conditions for a pawl sliding over the
ratchet teeth are obtained when , where ρ is
bend


 
ratchet teeth are obtained when , where ρ is
the friction angle.

 
Pawl Sliding over the Ratchet
10

11. ii. Friction Arresters
• Friction arresters operate noiselessly compared to
the operation of toothed arresting gear. However,
the pressure on the pawl pivot and shaft is
considerably high. Thus they have a limited
application.
application.
Friction Arrester
The force on the pawl
pivot is :


tan
F
F0
11

12. iii. Roller Ratchets
• A roller wedged between the follower and the driver
is subject to the action of normal forces and
and tangential friction forces and . With
the roller in equilibrium, the resultant force .
For equilibrium; thus .
1
N 2
N
1
1 N
 2
2 N

2
1 R
R 
2
1 N
N 
Design Diagram of a Ratchet Roller
12

13. The transmitted torque is








2
D
N
z
T 2
2
where z = number of rollers (usually z = 4)
06
.
0


for the roller and the driver and
 for the roller and the driver and
2
 for the roller and the follower)
1

for
When 2
tan
tan




 (the case of locking)
2
tan
zD
T
2
N


 
2
1 N
N
N 
 13

14. The length of the roller is
p
N
l 
Where, p = linear unit pressure, and its allowable
value is 450 kg/cm for hardened quality steel
value is 450 kg/cm for hardened quality steel
(e.g.: C15...C60).
14

15. • Brakes can be classified based on three
purpose as
– Parking (holding) brakes
– Lowering brakes
– Lowering brakes
– Combined holding and lowering brakes
– Based on the operational aspect
• Operated brakes
• Automatic brakes 15

16. i) Single Shoe Brakes
They are used to retard or stop unidirectional motions.
The pressure exerted by the cast iron shoe on the brake
wheel should be such that the friction force produced
A. Shoe brakes
wheel should be such that the friction force produced
on the surface of the wheel counter balance the
peripheral force
F
D
T
2
N 

 
16

17. N
A c tin g o n th e D ru m
N
l
A c tin g o n th e D ru m
 N
P
F
P
N
A c tin g o n th e D ru m
P
N
F
N
F
Diagrams of Single Shoe Brakes
A ctin g o n th e S h o e
A c tin g o n th e S h o e
b
l
a
A c tin g o n th e S h o e
b = 0
b
N
  N N
I
I I
(a ) (b ) (c )
17

18. • Force P at the end of the brake lever depends on the
position of pivot I. The friction force acts relative to
the brake wheel in a direction opposite to F.
For case (a), taking moment about I,
For case (a), taking moment about I,
0
a
N
b
N
l
P
0
M I 









+ counter clockwise & - clockwise
 
b
a
l
N
l
Nb
aN
P 




 18

19. but F
N 



F
N
;
 
b
a
l
F
P 


 







 b
a
l
F
P 

where the upper sign refers to counter
where the upper sign refers to counter
clockwise wheel rotation
For case (b),
l
Fa
l
a
N
P



19

20. but F
N 



F
N
;
 
b
a
l
F
P 


 







 b
a
l
F
P 

where the upper sign refers to counter
where the upper sign refers to counter
clockwise wheel rotation
For case (b),
l
Fa
l
a
N
P



20

21. • For case (c), 








 b
a
l
F
P

In actual designs the self-braking effect should
be avoided for single shoe brakes i.e. cases (a)
be avoided for single shoe brakes i.e. cases (a)
and (c) act arresters when

a
b 
This does not happen in the case of (b). 21

22. ii. Double Shoe Brakes
Diagram of a Shoe Brake
Applied by a Weight
22

23. • The total peripheral braking force produced by both
shoes in the rubbing surface is:
D
M
2
T br

Force to apply the brake force 1
F is:
    D
D
1
   
2
D
N
N
M
2
D
T
T 2
1
br
2
1 





 
2
1 N
N
2
D



Taking moments about the pivots:
0
b
N
N
F 1
1
1
1 


 
 23

24. i.e., normal force on the left
lever shoe and in the same way
b
F
N
1
1
1





b
F
N
1
1
2

















b
F
b
F
2
D
M
1
1
1
1
br



















b
1
b
1
2
DF
1
1
1






2
2
2
1
1
1
b
2
2
DF








2
2
2
1
1
1
b
DF






1
2
2
2
1
br
1
b
D
M
F

 




 

 1
br
D
M



2
2
b
 (is a small value)
24

25. • Unit pressure between the wheel and the
shoe of the left lever is:
A
N
p 1
 , where A = shoe bearing area
• Normal force on the right lever shoe is:
b
F
N
1
1
2




  
1
1
br
2
b
D
M
N

 





25

26. B. Band Brakes
• In band brakes the braking torque is obtained
due to friction of flexible band over the
surface of a brake wheel.
• The resistance of friction due to friction
acting on the surface of contact with the
acting on the surface of contact with the
drum is equal to the difference in the forces
on the band ends, and this force equalises the
peripheral force F, i.e.
off
on S
S
F 
 26

27. Diagrams for Determining Tension in the Band and Unit Pressure on the Drum
27

28. • From Euler's formula:


 e
S
S off
on   

 e
F
S on





 e
F
e
S
S on
on
  


 Fe
1
e
S on
,
on
on
 
on
1
e
Fe
S on

 

F
e
e
F
F
S
S on
off 





1


,











 


1
e
1
e
e
F
S off
1
e
F
S off

 
,
28

29. i. Simple Band Brakes
1
e
F
S off

 
Peripheral force is:
D
M
2
F br

br
M = actual braking torque 29

30. ii. Differential Band Brakes
Moment equation relative to the pivot:
0
a
S
a
S
F 1
on
2
off 



The braking effort F is
The braking effort F is

1
on
2
off a
S
a
S
F



1
off
2
off a
e
S
a
S 


 

1
2
off a
e
a
S 


30

31. iii.Additive-Action Band Brake
The moment equation at the pivot is
0




 a
S
a
S
F off
on

 
off
on S
S
a
F 


 
off
off S
e
S
a

 

 
1
e
aS off

 

 
 
1
1


 

e
e
P
a

31

32. The travel of the brake lever h is given by
a
2
h


 b
R
S
p n
0
max


32

33. Thermal Calculations of Shoe Brakes
i. Energy Absorbed by the Brake
• The kinetic energy of the body is absorbed by the
brake,
Pure translation  
2
2
2
/
1 v
v
m
E 

Pure translation
Pure rotation
Combination of translation and rotation
 
2
2
2
1
1 2
/
1 v
v
m
E 

 
2
2
2
1
2 2
/
1 
 
 I
E
2
1 E
E
E 

33

34. • Objects being lowered:
• Total Energy absorbed by the brake:
•The Energy absorbed by the brake wheel and transformed into
 
2
1
3 h
h
mg
E 

3
2
1 E
E
E
E 


•The Energy absorbed by the brake wheel and transformed into
heat must be dissipated to the surrounding air in order to avoid
excessive temperature rise in the brake lining.
• The heat dissipated may be estimated by
  r
d A
t
t
C
H 2
1 
 34

35. C = heat dissipation factor/ coefficient of heat transfer.
= temperature difference b/n the exposed radiating
surface and the surrounding air.
= area of radiating surface.
• The rise in the temperature of the brake drum
 
2
1 t
t 
r
A
= Heat generated by the brake
c = specific heat of the material of the brake drum
m = mass of the brake
c
m
H
t g .
/


g
H
35