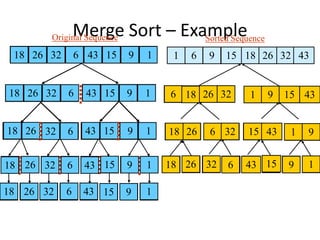
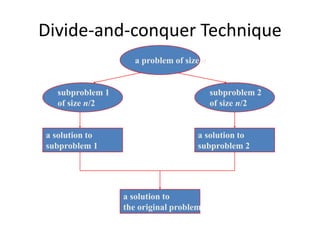
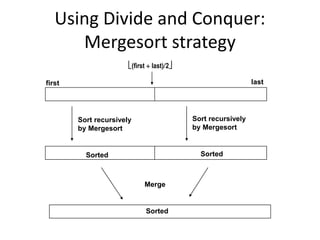
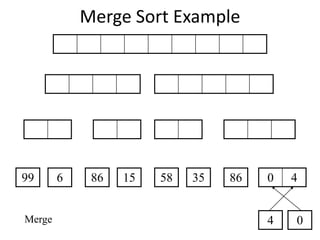
The document explains the merge sort algorithm, which is a divide and conquer sorting technique that recursively splits an unsorted list into two halves, sorts each half, and then merges them back together. It includes examples and a C++ program demonstrating how the algorithm works and its performance analysis with a time complexity of O(n log n) for worst, average, and best cases.

1. Merge Sort

2. Divide And Conquer
• Merging two lists of one element each is the same as
sorting them.
• Merge sort divides up an unsorted list until the
above condition is met and then sorts the divided
parts back together in pairs.
• Specifically this can be done by recursively dividing
the unsorted list in half, merge sorting the left side
then the right side and then merging the left and
right back together.

3. Mergesort Example
8 2 9 4 5 3 1 6
8 2 1 6
9 4 5 3
8 2 9 4 5 3 1 6
2 8 4 9 3 5 1 6
2 4 8 9 1 3 5 6
1 2 3 4 5 6 8 9
Merge
Merge
Merge
Divide
Divide
Divide
1 element
8 2 9 4 5 3 1 6

4. Merge Sort – Example
18 26 32 6 43 15 9 1
18 26 32 6 43 15 9 1
18 26 32 6 43 15 9 1
26
18 6
32 15
43 1
9
18 26 32 6 43 15 9 1
18 26 32 6 43 15 9 1
18 26 32
6 15 43 1 9
6 18 26 32 1 9 15 43
1 6 9 15 18 26 32 43
18 26
18 26
18 26
32
32
6
6
32 6
18 26 32 6
43
43
15
15
43 15
9
9
1
1
9 1
43 15 9 1
18 26 32 6 43 15 9 1
18 26 6
32
6
26 32
18
15
43 1
9
1 9
15 43
1
6 9 15
18 26 32 43
Original Sequence Sorted Sequence

5. Divide-and-conquer Technique
subproblem 2
of size n/2
subproblem 1
of size n/2
a solution to
subproblem 1
a solution to
the original problem
a solution to
subproblem 2
a problem of size n

6. Using Divide and Conquer:
Mergesort strategy
Sorted
Merge
Sorted Sorted
Sort recursively
by Mergesort
Sort recursively
by Mergesort
first last
(first  last)2

7. Merge Sort Algorithm
• Divide: Partition ‘n’ elements array into two
sub lists with n/2 elements each
• Conquer: Sort sub list1 and sub list2
• Combine: Merge sub list1 and sub list2

8. Merge Sort Example
99 6 86 15 58 35 86 4 0

9. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0

10. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 15
99 6 58 35 86 4 0

11. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 15
99 6 58 35 86 4 0
99 6 86 15 58 35 86 4 0

12. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 15
99 6 58 35 86 4 0
99 6 86 15 58 35 86 4 0
4 0

13. Merge Sort Example
99 6 86 15 58 35 86 0 4
4 0
Merge

14. Merge Sort Example
15 86
6 99 35 58 0 4 86
99 6 86 15 58 35 86 0 4
Merge

15. Merge Sort Example
6 15 86 99 0 4 35 58 86
15 86
6 99 35 58 0 4 86
Merge

16. Merge Sort Example
0 4 6 15 35 58 86 86 99
6 15 86 99 0 4 35 58 86
Merge

17. Merge Sort Example
0 4 6 15 35 58 86 86 99

18. Program
#include<iostream.h>
#include<conio.h>
class MS
{
private:
int A[10];
public:
int n;
int low, high;
void get_data();
void Mergesort(int low, int high);
void Combine(int low, int mid, int high);
void Display();
};
void MS::get_data()
{
cout<<"n Enter the length of the list";
cin>>n;
cout<<"n Enter the list elements: n";
for(int i = 0; i<n; i++)
{
cin>>A[i];
}
}
void MS::Mergesort(int low, int high)
{
int mid;
if(low<high)
{
mid = (low+high)/2; //split the list at mid
Mergesort(low, mid); //first sublist
Mergesort(mid+1, high); //second sublist
Combine(low, mid, high); //merging two sublists
}
}

19. Program
void MS::Combine(int low, int mid, int high)
{
int i,j,k;
int temp[10];
i = low;
j = mid+1;
k = low;
while(i <= mid && j <= high)
{
if(A[i] <= A[j])
{
temp[k] = A[i];
i++;
k++;
}
else
{
temp[k] = A[j];
j++;
k++;
}
}
while(i<=mid)
{
temp[k] = A[i];
i++;
k++;
}
while(j<=high)
{
temp[k] = A[j];
j++;
k++;
}
for(k = low; k <= high; k++)
{
A[k] = temp[k];
}
}

20. Program
void MS::Display()
{
cout<<"n The sorted array is:n";
for(int i = 0; i<n; i++)
{
cout<<" "<<A[i];
}
}
int main()
{
MS obj;
obj.get_data();
obj.low=0;
obj.high=(obj.n)-1;
obj.Mergesort(obj.low, obj.high);
obj.Display();
getch();
return 0;
}

21. Time Complexity Analysis
• Worst case: O(nlog2n)
• Average case: O(nlog2n​​)
• Best case: O(nlog2n​​)