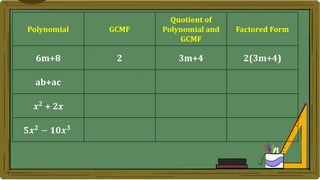
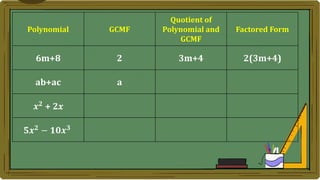
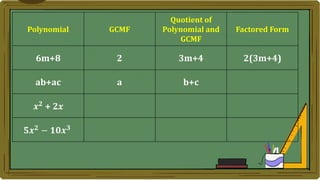
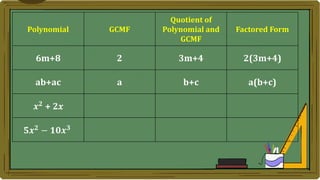
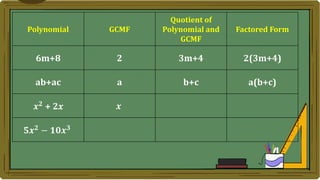
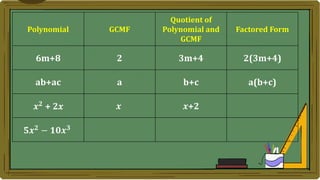
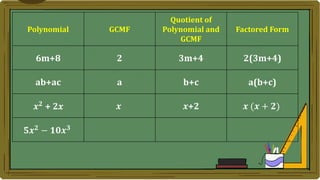
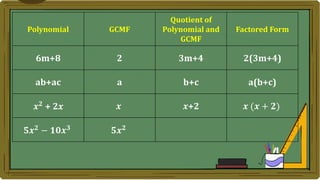
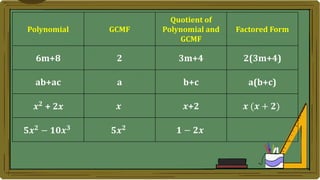
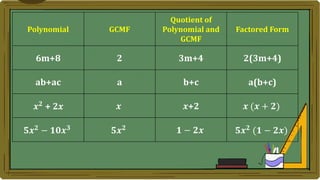
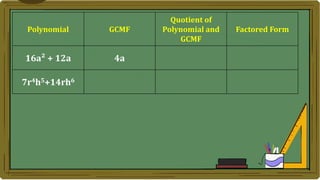
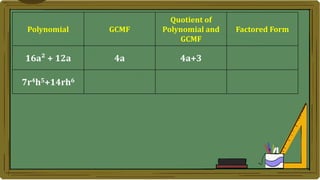
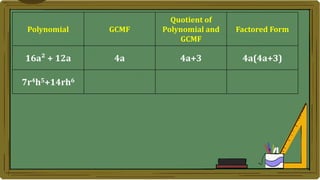
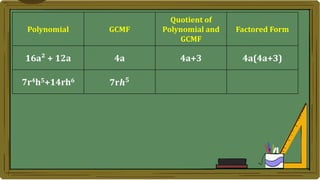
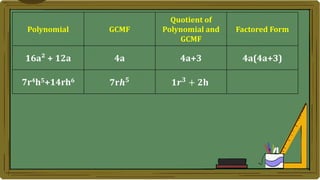
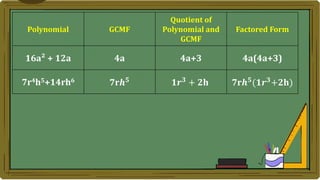
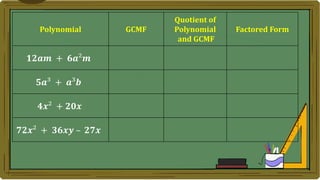
Algebra generalizes arithmetic by using symbols like letters and numbers with operations. An algebraic expression combines these symbols according to the rules of arithmetic. Examples of algebraic expressions include a term, which is a constant, variable, or their product, and a polynomial, which is a sum of terms with whole number exponents. Factoring a polynomial involves finding the greatest common monomial factor and dividing each term by it to obtain the factored form.

1. Algebra is a branch of mathematics
which generalizes the facts of
arithmetic. The result of combining
symbols such as letters, numbers,
punctuations and operations of
arithmetic is called an algebraic
expression or simply an expression.

2. Some examples of algebraic expressions are:

3. A term is a constant or a variable or
constants and variables multiplied
together.
Examples:

4. A polynomial is an algebraic
expression that represents a
sum of one or more terms
containing whole-number
exponents on the variables.
What is a polynomial?

5. Here are some examples of polynomials:

10. Quarter 1
Factoring Polynomials

11. How to get the factors
of a given polynomial
with common
monomial factor?

12. 1.Obtain the greatest common monomial factor
of the terms of the polynomial. The greatest
common monomial factor is the first factor of
the polynomial.
2.The second factor of the polynomial is
obtained by dividing each term of the
polynomial by the greatest common monomial
factor (GCMF).

13. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2
ab+ac
𝒙𝟐
+ 2𝑥
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

14. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4
ab+ac
𝒙𝟐
+ 2𝑥
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

15. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac
𝒙𝟐
+ 2𝑥
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

16. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a
𝒙𝟐
+ 2𝑥
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

17. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c
𝒙𝟐
+ 2𝑥
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

18. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c a(b+c)
𝒙𝟐
+ 2𝑥
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

19. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c a(b+c)
𝒙𝟐
+ 2𝑥 𝒙
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

20. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c a(b+c)
𝒙𝟐
+ 2𝑥 𝒙 𝒙+2
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

21. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c a(b+c)
𝒙𝟐
+ 2𝑥 𝒙 𝒙+2 𝒙 (𝒙 + 𝟐)
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑

22. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c a(b+c)
𝒙𝟐
+ 2𝑥 𝒙 𝒙+2 𝒙 (𝒙 + 𝟐)
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑 𝟓𝒙𝟐

23. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c a(b+c)
𝒙𝟐
+ 2𝑥 𝒙 𝒙+2 𝒙 (𝒙 + 𝟐)
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑 𝟓𝒙𝟐 𝟏 − 𝟐𝒙

24. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
6m+8 2 3m+4 2(3m+4)
ab+ac a b+c a(b+c)
𝒙𝟐
+ 2𝑥 𝒙 𝒙+2 𝒙 (𝒙 + 𝟐)
𝟓𝒙𝟐 − 𝟏𝟎𝒙𝟑 𝟓𝒙𝟐 𝟏 − 𝟐𝒙 𝟓𝒙𝟐 (𝟏 − 𝟐𝒙)

25. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
16a² + 12a
7r4h5+14rh6

26. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
16a² + 12a 4a
7r4h5+14rh6

27. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
16a² + 12a 4a 4a+3
7r4h5+14rh6

28. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
16a² + 12a 4a 4a+3 4a(4a+3)
7r4h5+14rh6

29. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
16a² + 12a 4a 4a+3 4a(4a+3)
7r4h5+14rh6 7r𝒉𝟓

30. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
16a² + 12a 4a 4a+3 4a(4a+3)
7r4h5+14rh6 7r𝒉𝟓 𝟏𝒓𝟑
+ 𝟐𝐡

31. Polynomial GCMF
Quotient of
Polynomial and
GCMF
Factored Form
16a² + 12a 4a 4a+3 4a(4a+3)
7r4h5+14rh6 7r𝒉𝟓 𝟏𝒓𝟑
+ 𝟐𝐡 7r𝒉𝟓(𝟏𝒓𝟑+𝟐𝐡)

32. Polynomial GCMF
Quotient of
Polynomial
and GCMF
Factored Form
𝟏𝟐𝒂𝒎 + 𝟔𝒂²𝒎
𝟓𝒂³ + 𝒂³𝒃
𝟒𝒙² + 𝟐𝟎𝒙
𝟕𝟐𝒙² + 𝟑𝟔𝒙𝒚 – 𝟐𝟕𝒙

33. Study Math
for a
Better Path

34. A. Find the factors of the perfect
squares.
1. 16 4. 𝟗𝒚𝟒
2. 𝒙𝟐
5.
𝟏
𝟒
3. 𝟐𝟓𝒂𝟐
(Rewrite in exponential form)