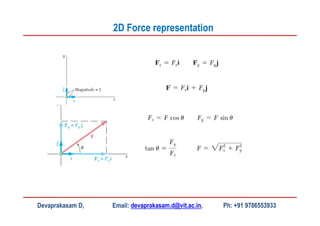
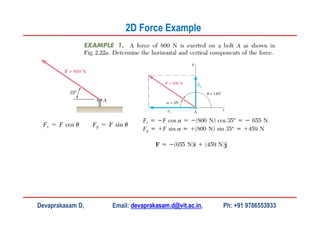
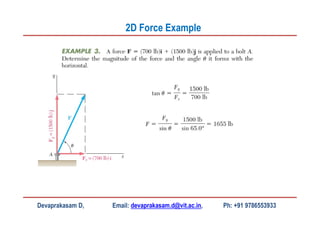
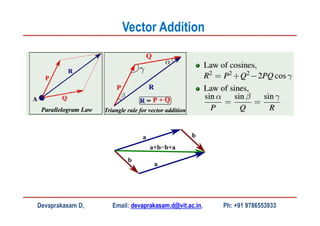
This document contains lecture slides from Professor Devaprakasam Deivasagayam on the topic of Engineering Mechanics. It introduces scalar and vector quantities, the concept of force as a vector, and how to represent forces in 2D and 3D using rectangular and parallel/perpendicular components. It also demonstrates how to use vector addition to find the resultant of multiple forces. Examples are provided for representing forces, resolving them into components, and adding vectors. Homework is assigned at the end.

1. DEVAPRAKASAM DEIVASAGAYAM
Professor of Mechanical Engineering
Room:11, LW, 2nd Floor
School of Mechanical and Building Sciences
Email: devaprakasam.d@vit.ac.in, dr.devaprakasam@gmail.com
MEE1002: Engineering Mechanics (2:1:0:0:3)
Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933

3. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Newtonian Mechanics

4. • Scalar Quantity- Has magnitude and has no associated direction
• Examples: Volume, Time, Mass, Speed, Density, Temperature.
• Vector Quantity- Has Magnitude and Direction
• Examples: Force, Velocity, Moment, Acceleration
Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Scalar and Vector

5. • Push or Pull on a body
• It is a vector
i
Y
X
Z
j
k
F = Fx i + Fy j ……(2D)
F = Fx i + Fy j + Fz k…..(3D)
Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Force
Sign Convention (+ve)

6. • Express the 2D and 3D equilibrium equations
for particle resulting from the application of
Newton’s 1st Law
0
0
0






Y
X
F
F
F
3D
0
0
0
0








Z
Y
X
F
F
F
F
2D
0
0
0
|| 






F
F
F
2 Independent Eqns & 3 Independent Eqns &
Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D and 3D Equilibrium

7. • Express a 2D force in terms of rectangular.
components.
• Express a 2D force in terms of parallel and
perpendicular components.
• Apply vector addition to find resultant of more
than one force.
X
F
i
Y
j
θ
F = Fx i + Fy j
Fx= F cosθ
Fy= F sinθ
Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force representation

8. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force representation

9. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force Example

10. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force Example

11. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force Example

12. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force Example

13. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force Example

14. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
2D Force Example

15. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Vector Addition

16. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Vector addition Example

17. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Vector addition Example

18. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Vector addition Example

19. Devaprakasam D, Email: devaprakasam.d@vit.ac.in, Ph: +91 9786553933
Home Work