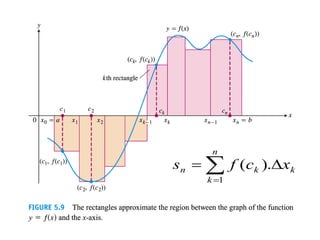
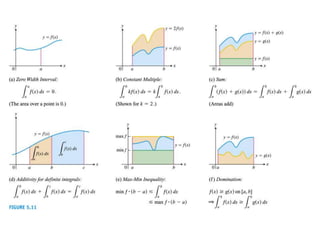
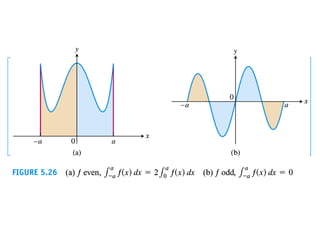
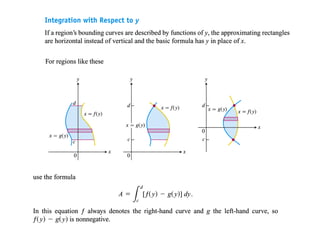
The document discusses the process of estimating areas under curves using definite integrals, featuring multiple examples of calculating such areas using different functions. It highlights key steps, including sketching the curves, determining integration limits, and applying integration techniques. Additionally, it presents various scenarios involving intersections and areas bounded by curves.

1. Integration
Introduction

2. Estimating with Finite Sums

7. 



n
k
k
k
n x
c
f
s
1
).
(

8. The Definite Integral

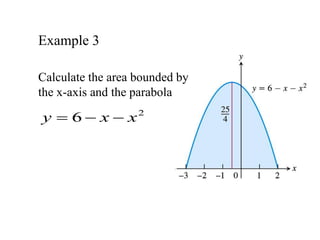
16. Example 1
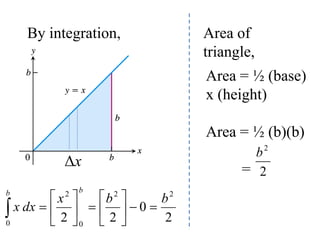
Find the area A under
y = x over the interval
[0,b], b > 0

17. By integration,
Δx
2
0
2
2
2
2
0
0
2
b
b
x
dx
x
b
b

















Area of
triangle,
Area = ½ (base)
x (height)
Area = ½ (b)(b)
= 2
2
b

18. By integration,
Similarly,

21.  
2
5
2
3
-
4(3)
3
1
2
4
3
1
x
-
4
3
1
)
(
1
Average
2
3
0
2
3
0





















x
x
dx
dx
x
f
a
b
b
a
Example 2

22. Example 3
Calculate the area bounded by
the x-axis and the parabola
2
6 x
x
y 



23. Solution:
2
3
2
3
3
2
2
3
2
6
)
6
(


 










x
x
x
dx
x
x



















3
27
2
9
18
3
8
2
12
6
5
20


24. Example 4
2
1
2
)
(
of
graph
the
and
axis
-
between x
region
the
of
area
the
Find
2
3






x
x
x
x
x
f

25. 12
5
3
4
)
2
(
:
0
1
2
3
4
0
1
2
3















x
x
x
dx
x
x
x
Solution
3
8
3
4
)
2
(
2
0
2
3
4
2
0
2
3














x
x
x
dx
x
x
x
2
units
12
37
3
8
12
5
area
enclosed
Total 




26. Definite integral

27. Area under the
curve

29.  

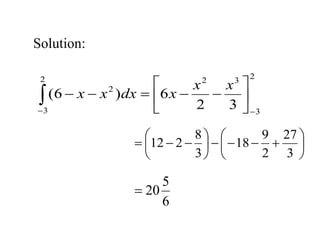
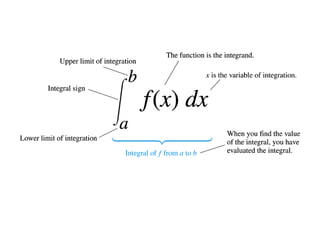
b
a
dx
x
g
x
f
Area )]
(
)
(
[

30. Find the solution by 3 steps:
1. Sketch the curves and shade the required
area.
2. Find the limits of integration by solving
simultaneous equations.
3. Calculate the area.
Find the area enclosed by the parabola y=2 – x2
and the line y = – x.
Example 5

31. origin
through
passing
slope
negative
line
straight
axis
-
y
on
intercept
c
slope,
m
where
,
line
straight
of
Equation
:
Revision









x
y
c
mx
y
y
x
y = – x

32. 2
,
0
when
:
axis
-
on x
on
intersecti
Find
2
,
0
when
:
axis
-
y
on
on
intersecti
Find
2 2







x
y
y
x
x
y
y
x

33. (minima)
positive
(maxima),
negative
when
:
Note
(maxima)
2
(0,2)
point
turning
2
,
0
when
0
,
0
when
(slope)
2
2
2
2
2
2
2













dx
y
d
dx
y
d
y
x
x
dx
dy
x
dx
dy
x
y
y
x

34. )
2
(2,
and
1)
,
1
(
are
points
on
Intersecti
2
2
When
1
1
When
2
,
1
0
)
2
)(
1
(
0
2
2
:
and
2
for
Solve
:
curves
2
between
points
on
intersecti
Finding
2
2
2
























, y
x
, y
x
x
x
x
x
x
x
x
x
x
y
x
y

35. Combining both
graphs,
Note:
- Slope of curves
- Turning point
- Maxima
- Intersection points

36. 2
2
1
3
2
2
1
2
2
1
2
unit
2
9
3
1
2
1
2
3
8
2
4
4
3
2
2
)
2
(
)]
(
)
2
[(
)]
(
)
(
[












































x
x
x
dx
x
x
dx
x
x
dx
x
g
x
f
A
b
a
Solution for
area between
2 curves:

37. Example 6
6.

38. Solution:
Area A
Limits of integration are a=0, b=2.
Area B
Solving simultaneously 2
and 

 x
y
x
y
4
,
1
0
)
4
)(
1
(
0
4
5
4
4
)
2
(
2
2
2













x
x
x
x
x
x
x
x
x
x

39. 3
10
)
2
(
area
Total
4
2
2
0




 
 dx
x
x
dx
x
2)
-
(x
-
)
(
)
(
:
4
2
For
)
(
)
(
:
2
0
For
4
limit
hand
Right
x
x
g
x
f
x
x
x
g
x
f
x










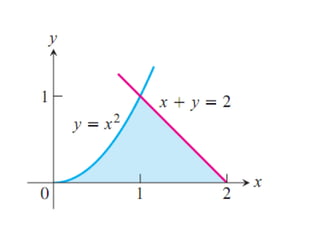
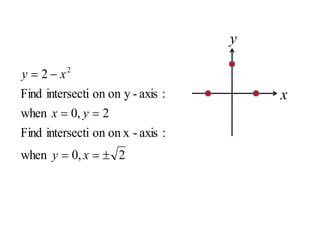
42. Solution:
Solving simultaneous equation of
gives roots y=-1, y=2.
Limits a=0,b=2.
2
and
2


 y
x
y
x
3
10
)
2
(
)]
(
)
(
[
2
0
2








dy
y
y
dy
y
g
y
f
A
b
a