Downloaded 38 times
Uploaded byTheo Schlossnagle
The math behind big systems analysis.
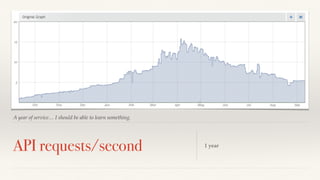
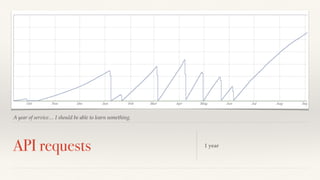
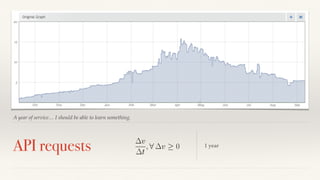
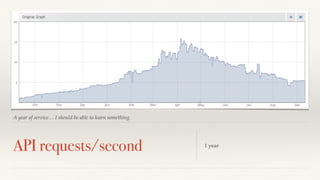
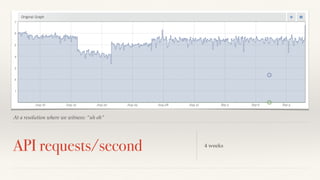
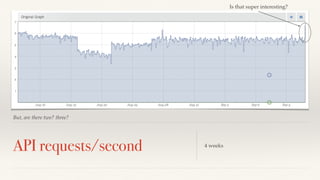
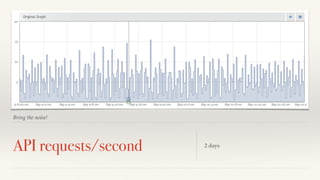
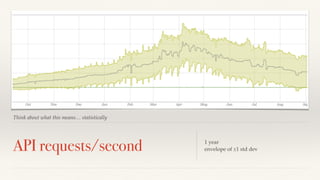
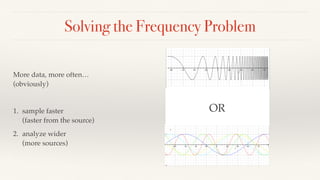
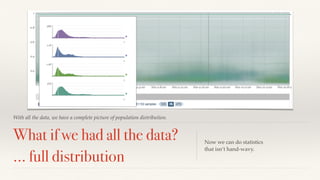
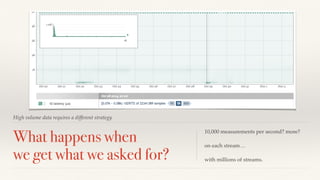
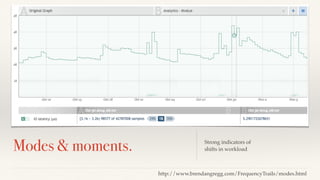
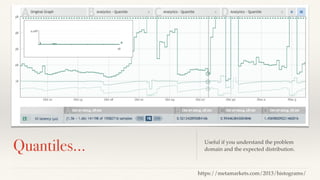
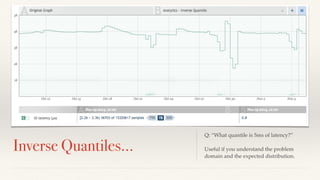
The document discusses mathematical methods for analyzing systems telemetry data, addressing issues such as signal classification, offline modeling, and online fault detection in the context of big data. It emphasizes the importance of statistical models and how they can be challenged by infrequent data and deviations from normal distributions, leading to the need for alternative approaches like the tukey test. Overall, it highlights the necessity of adapting algorithms to handle high-frequency data efficiently while ensuring reliable and repeatable outcomes.
More Related Content
Similar to The math behind big systems analysis.
The math behind big systems analysis.
- 1. A tour throughmathematical methods on systems telemetry Math in Big Systems If it was a simple math problem, we’d have solved all this by now.
- 2. The many facesof Theo Schlossnagle @postwait CEO Circonus
- 3. Choosing an approachis premature… Problems How do we determine the type of signal? How do we manage off-line modeling? How do we manage online fault detection? How do we reconcile so users don’t hate us? How we we solve this in a big-data context?
- 4. Picking an Approach Statistical? Machine learning? Supervised? Ad-hoc? ontological? (why it is what it is)
- 5. tl;dr Apply PhDsApply PhDs Rinse Wash Repeat
- 6. Garbage in, categoryout. Classification Understanding a signal We found to be quite ad-hoc At least the feature extraction
- 7. A year ofservice… I should be able to learn something. API requests/second 1 year
- 8. A year ofservice… I should be able to learn something. API requests 1 year
- 9. A year ofservice… I should be able to learn something. API requests 1 year Δv Δt , ! Δv ≥ 0
- 10. Some data goesboth ways… Complicating Things Imagine disk space used… it makes sense as a gauge (how full) it makes sense as rate (fill rate)
- 11. Error + error+ guessing = success How we categorize Human identify a variety of categories. Devise a set of ad-hoc features. Bayesian model of features to categories. Human tests. https://www.flickr.com/photos/chrisyarzab/5827332576
- 12. Many signals havesignificant noise around their averages Signal Noise A single “obviously wrong” measurement… is often a reasonable outlier.
- 13. A year ofservice… I should be able to learn something. API requests/second 1 year
- 14. At a resolutionwhere we witness: “uh oh” API requests/second 4 weeks
- 15. But, are theretwo? three? API requests/second 4 weeks Is that super interesting?
- 16. Bring the noise! API requests/second 2 days
- 17. Think about whatthis means… statistically API requests/second 1 year envelope of ±1 std dev
- 18. Lies, damned lies,and statistics Simple Truths Statistics are only really useful with p-values are low. p ≤ 0.01 : very strong presumption against null hyp. 0.01 < p ≤ 0.05 : strong presumption against null hyp. 0.05 < p ≤ 0.1 : low presumption against null hyp. p > 0.1 : no presumption against the null hyp. from xkcd #882 by Randall Munroe
- 19. What does ap-value have to do with applying stats? The p-value problem It turns out a lot of measurement data (passive) is very infrequent. 60% of the time… it works every time.
- 20. Our low frequencieslead us to questions of doubt… Given a certain statistical model: How many few points need to be seen before we are sufficiently confident that it does not fit the model (presumption against the null hypothesis)? With few, we simply have outliers or insignificant aberrations. http://www.flickr.com/photos/rooreynolds/
- 21. Solving the FrequencyProblem More data, more often… (obviously) 1. sample faster (faster from the source) 2. analyze wider (more sources) OR
- 22. https://www.flickr.com/photos/whosdadog/3652670385 Increasing frequencyis the only option at times. Signals of Importance Without large-scale systems We must increase frequency
- 23. What do meanthat my mean is mean? Why can’t math be nice to people? https://www.flickr.com/photos/imagesbywestfall/3606314694 Most algorithms require measuring residuals from a mean Mean means Calculating means is “easy” There are some pitfalls
- 24. Newer data shouldinfluence our model. Signals change The model needs to adapt. Exponentially decaying averages are quite common in online control systems and used as a basis for creating control charts. Sliding windows are a bit more expensive.
- 25. EWM vs. SWM ❖ EWM : ST ❖ S1 = V1 ❖ ST = 훼VT + (1-훼)ST-1 ❖ Low computation overhead ❖ Low memory usage ❖ Hard to repeat offline ❖ SMW tracking the last N values : ST ❖ ST = ST-1 - VT-N/n + VT/n ❖ Low computational overhead ❖ High memory usage ❖ Easy to repeat offline
- 26. Repeatable outcomes areneeded In our system… We need our online algorithms to match our offline algorithms. This is because human beings get pissed off when they can’t repeat outcomes that woke them up in the middle of the night. EWM: not repeatable SWM: expensive in online application
- 27. Repeatable, low-cost slidingwindows Our solution: lurching windows fixed rolling windows of fixed windows SWM + EWM
- 28. Putting it alltogether… How to test if we don’t match our model?
- 29.
- 30.
- 31. Applying CUSUM APIrequests/second 4 weeks CUSUM Control Chart
- 32. Can we dobetter? Investigations The CUSUM method has some issues. It’s challenging when signals are noise or of variable rate. We’re looking into the Tukey test: • compares all possible pairs of means • test is conservative in light of uneven sample sizes https://www.flickr.com/photos/st3f4n/4272645780
- 33. All that workand you tell me *now* that I don’t have a normal distribution? Most statistical methods assume a normal distribution. Your telemetry data has never been evenly distributed Statistics suck. https://www.flickr.com/photos/imagesbywestfall/3606314694 All this “deviation from the mean” assumes some symmetric distribution.
- 34. Think about whatthis means… statistically Rather obviously not a normal distribution The average minus the standard deviation is less than zero on a measurement that can only be ≥ 0.
- 35. With all thedata, we have a complete picture of population distribution. What if we had all the data? … full distribution Now we can do statistics that isn’t hand-wavy.
- 36. High volume datarequires a different strategy What happens when we get what we asked for? 10,000 measurements per second? more? on each stream… with millions of streams.
- 37. Let’s understand thescope of the problem. First some realities This is 10 billion to 1 trillion measurements per second. At least a million independent models. We need to cheat. https://www.flickr.com/photos/thost/319978448
- 38. https://www.flickr.com/photos/meddygarnet/3085238543 When wehave too much, simplify… Information compression We need to look to transform the data. Add error in the value space. Add error in the time space.
- 39. Summarization & Extraction âť– Take our high-velocity stream âť– Summarize as a histogram over 1 minute (error) âť– Extract useful less-dimensional characteristics âť– Apply CUSUM and Tukey tests on characteristics
- 40. Lorem Ipsum Dolor Modes & moments. Strong indicators of shifts in workload http://www.brendangregg.com/FrequencyTrails/modes.html
- 41. Lorem Ipsum Dolor Quantiles… Useful if you understand the problem domain and the expected distribution. https://metamarkets.com/2013/histograms/
- 42. Lorem Ipsum Dolor Inverse Quantiles… Q: “What quantile is 5ms of latency?” Useful if you understand the problem domain and the expected distribution.
- 43. Thank ou! andthank you to the real brains behind Circonus’ analysis systems: Heinrich and George.