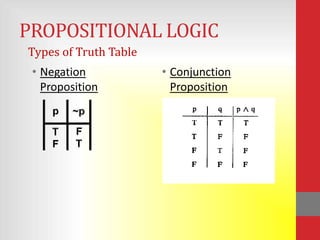
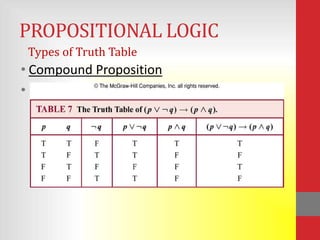
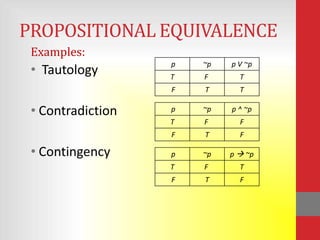
The document discusses propositional logic and covers topics like propositional variables, truth tables, logical equivalence, predicates, and quantifiers. It defines key concepts such as propositions, tautologies, contradictions, predicates, universal and existential quantifiers. Examples are provided to illustrate different types of truth tables, logical equivalences like De Morgan's laws, and uses of quantifiers.

1. TAF 3023: DISCRETE
MATH
Power !

2. PROPOSITIONAL LOGIC
Proposition • possible condition of the world
about which we want to say
something.
Example • Apple is a fruit.

3. PROPOSITIONAL LOGIC
• Propositional • A proposition or statement is a
logic sentence which is either true or
false.
• Example • True - Apple is a fruit.
• False - Rice is a fruit.

4. PROPOSITIONAL LOGIC
• Propositional • Propositional variables use letters to
variables represent it, just as letters used to
represent numerical variables.
• Example • p, q, r, s, ………

5. PROPOSITIONAL LOGIC
Types of Truth Table
• Negation • Conjunction
Proposition Proposition

6. PROPOSITIONAL LOGIC
Types of Truth Table
• Disjunction • Exclusive Or of Two
Proposition Propositions

7. PROPOSITIONAL LOGIC
Types of Truth Table
• Conditional Statement and Biconditional
Statement
•

8. PROPOSITIONAL LOGIC
Types of Truth Table
• Compound Proposition
•

9. PROPOSITIONAL EQUIVALENCE
• Tautology
 a compound proposition that is always true.
• Contradiction
 a compound proposition that is always false.
• Contingency
 a compound proposition that contain neither true or
false that mean in its truth table have at least one true
and at least one false.

10. PROPOSITIONAL EQUIVALENCE
Examples:
p ~p p V ~p
• Tautology T F T
F T T
• Contradiction p ~p p ^ ~p
T F F
F T F
• Contingency p ~p p  ~p
T F T
F T F

11. LOGICAL EQUIVALENCE
• In logic, statements p and q are logically equivalent if
they have the same logical content
• (Mendelson 1979:56) two statements are equivalent if
they have the same truth value in every model
• Logical Equivalence Table

12. LOGICAL EQUIVALENCE
De Morgan’s Law
• Probably the most important logical
equivalence
 ￢(p ∧ q) ≡ ￢p ∨￢q
 ￢(p ∨ q) ≡ ￢p ∧￢q

13. PREDICATE AND QUANTIFIERS
Introduction:
• Predicate is an open statement or sentence that contains a finite
numbers of variables. Predicates become statement when specifies
values are substituted for the variables by certain allowable choices
of value.
• variable x - subject
Example: • greater than 3 – predicate
“x is greater
than 3” • predicate in the form of:
 P(x) – this is a unary predicate (has one
OR variable)
 P( x, y) – this is a binary predicate (has
• denote as P(x) two variables)
 P(x1, x2, x…….., xn) – this is an n-ary or n-
place predicate – (has n individual
variables in a predicate)

14. PREDICATE AND QUANTIFIERS
Quantifiers:
• Definition • a logical symbol which makes an assertion
about the set of values which make one or
more formulas true.
• universal quantifier: read for
“all”, “each”, “every”.
• existential quantifier: read for “some”
statement that is true or false.
• Example • universal - “Everyone likes cakes“.
“Not everyone likes cakes”.
• existential - “Someone likes cakes”.
“No one likes cakes”.

15. PREDICATE AND QUANTIFIERS
Examples Using Quantifiers:
Universal and Existential Quantifier
Statement: True: False:
∀xP(x) P(x) is true for every There is an x for
x. which P(x) is false.
∃xP(x) There is an x for P(x) is false for every
which P(x) is true. x.

16. PREDICATE AND QUANTIFIERS
Examples Using Quantifiers:
Universal and Existential Quantifier
Statement: True: False:
∀xP(x) x+1>x x<2
If P(x) = 1, the If P(x) = 1 or 0, the
quantification is quantification is true.
true. But If P(x) = 3, the
quantification is false.
∃xP(x) x>3 x=x+1
If P(x) = 4, the P(x) is false for all real
quantification is number.
true.