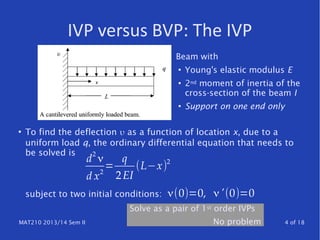
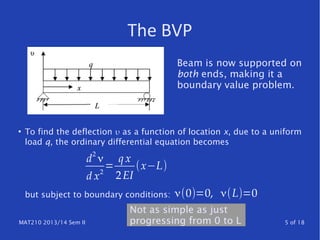
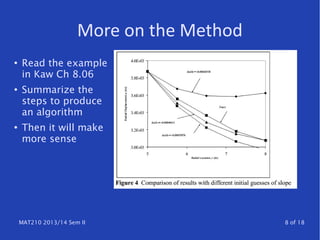
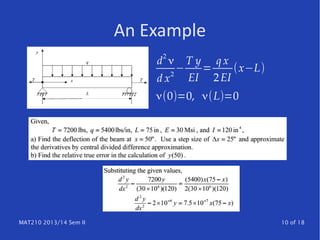
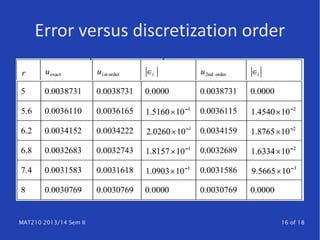
The document discusses techniques for solving differential equations, particularly focusing on boundary value problems (BVPs) using methods like the shooting method and finite difference methods. It details how to transition from initial value problems (IVPs) to BVPs and provides insights into algorithmic approaches for these techniques. Additionally, it highlights error analysis and the structure of finite difference matrices.

1. St. John's University of Tanzania
MAT210 NUMERICAL ANALYSIS
2013/14 Semester II
DIFFERENTIAL EQUATIONS
Boundary Value Problems
Kaw, Chapter 8.06-8.07
Some parts of this presentation are based on resources at
http://nm.MathForCollege.com, primarily
http://http://mathforcollege.com/nm/mtl/gen/08ode/index.html

2. MAT210 2013/14 Sem II 2 of 18
Ordinary Differential Equations
● Topics
●
1st order ODE
– Euler's Method 
– Runge-Kutta Methods 
● Higher order Initial Value
●
Higher order Boundary Value
– Shooting Method
– Finite Differences
Today's discussion
….Read Kaw 8.05

3. MAT210 2013/14 Sem II 3 of 18
Beyond First Order
●
2nd order ODE's
●
Require 2 conditions
– Two initial: y(x0) and y'(x0) – still an IVP
– Two boundaries: y(x0) and y(x1) – now a BVP
●
Kaw 8.05 describes how to decompose the 2nd
order IVP into two 1st order IVPs and use Euler or
Runge-Kutta to solve
●
Boundary Value Problems require something more
– The Shooting Method extension of the IVP techniques
– The Finite Difference Method

4. MAT210 2013/14 Sem II 4 of 18
IVP versus BVP: The IVP
●
To find the deflection υ as a function of location x, due to a
uniform load q, the ordinary differential equation that needs to
be solved is
subject to two initial conditions:
d
2
ν
d x2
=
q
2EI
(L−x)2
ν(0)=0, ν'(0)=0
Beam with
●
Young's elastic modulus E
●
2nd moment of inertia of the
cross-section of the beam I
●
Support on one end only
Solve as a pair of 1st order IVPs
No problem

5. MAT210 2013/14 Sem II 5 of 18
The BVP
●
To find the deflection υ as a function of location x, due to a uniform
load q, the ordinary differential equation becomes
but subject to boundary conditions:
d
2
ν
d x2
=
q x
2EI
(x−L)
ν(0)=0, ν(L)=0
Beam is now supported on
both ends, making it a
boundary value problem.
Not as simple as just
progressing from 0 to L

6. MAT210 2013/14 Sem II 6 of 18
The Shooting Method
● Why not approach the BVP using the IVP
techniques, replacing one boundary
condition with a “guess” of another initial
condition that causes the IVP solution to
“hit” the other boundary condition?
● Progressively refine the guess until it hits
● Refinement could be through interpolation
– Aha, a combination of techniques to reach the
desired objective
● This is the Shooting Method

7. MAT210 2013/14 Sem II 7 of 18
Summary of the Method
● Use y(x0) and a reasonable guess for y'(x0)
● Usually y'(x0)≈(y(x1)-y(x0))/(x1-x0) … FDA
●
Use Runge-Kutta to “shoot” to an
approximation for y(x1)
● If close enough, then stop, solution is done
● If not, pick another y(x0) and repeat Runge-Kutta
to get a second approximation for y(x1)
● Now use interpolation for 3rd guess
● Repeat the process until solution “hits” y(x1)

8. MAT210 2013/14 Sem II 8 of 18
More on the Method
●
Read the example
in Kaw Ch 8.06
●
Summarize the
steps to produce
an algorithm
●
Then it will make
more sense

9. MAT210 2013/14 Sem II 9 of 18
The Finite Difference Method
● Why guess and correct?
Why not feed the information from the
other boundary condition back through the
intervals?
●
That is the heart of the Finite Difference
(FD) Method
● Create a set of problems where the
subintervals share a boundary condition
● End up with a linear algebra problem

10. MAT210 2013/14 Sem II 10 of 18
An Example
d
2
ν
d x2
−
T y
EI
=
q x
2EI
(x−L)
ν(0)=0, ν(L)=0

11. MAT210 2013/14 Sem II 11 of 18
Approximating the derivatives
●
Now apply the equation to each of the
interior nodes (2 & 3) and the boundary
conditions to end nodes (1 & 4)

12. MAT210 2013/14 Sem II 12 of 18
Node equations

13. MAT210 2013/14 Sem II 13 of 18
Solve in matrix form

14. MAT210 2013/14 Sem II 14 of 18
Examining the error
The exact solution:
The error calculation:
All in one step
●
Use a fast matrix
inversion method

15. MAT210 2013/14 Sem II 15 of 18
Finite Difference Errors
●
Truncation errors (aka Discretization Errors)
●
The approximation of the derivatives has an error, e.g. O(h)
●
Applying Fast Fourier Transforms can help, eg. spectral methods
Understand the problem, do some analysis, improve the discretization
●
Rounding errors:
●
The loss of precision due to computer rounding of decimal
quantities
●
Example, standard arithmetic is O(10-16/h)
●
Total error: Best accuracy is usually obtained when these
different error types match
– O(h) matches O(10 16− /h) when h≈10 8− , producing a total error around 10 8− .
– Higher derivatives: pth derivative rounding error typically O(10 16− /hp)
●
For this reason rarely use FD for derivatives beyond the third or fourth

16. MAT210 2013/14 Sem II 16 of 18
Error versus discretization order

17. MAT210 2013/14 Sem II 17 of 18
Structure of the FD matrix
1st
order
2nd
order
Always tridiagonal
– can use fast matrix solvers
– Thomas' algorithm

18. MAT210 2013/14 Sem II 18 of 18
Summary
● Finite difference (FD) methods can be used
for partial differential equations, too
●
There are a wide range of FD methods,
which use different approximations for the
derivatives, different matrix techniques,
different strategies for creating intervals or
grids/meshes for PDEs
●
More at
http://www.scholarpedia.org/article/Finite_difference_method