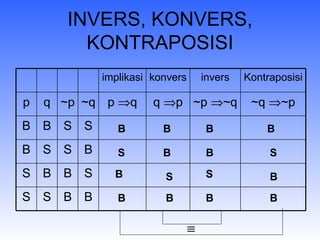
Dokumen ini membahas konsep logika matematika termasuk invers, konversi, kontraposisi, modus ponens, modus tolens, dan silogisme. Selain itu, dokumen ini memberikan contoh soal dan penjelasan tentang cara menarik kesimpulan logis dari pernyataan yang diberikan. Lima pernyataan mengenai atlet, musisi, dan kondisi lainnya juga dibahas dalam konteks argumen logis.

1. LOGIKA MATEMATIKA Pertemuan IV Invers, Konvers dan Kontraposisi, Modus Ponens, Tolens, dan Silogisme

2. Jawaban PR Lat 8 hal 241 no 4 Logis logis Tidak logis logis tidak logis Tidak logis

3. Lat 9 hal 244 1.f BBBBSSSS BSBSBSBS BBSSBBSS BBBBSSSS BBSSBBSS BBBBSSSS BSBSBSBS BSSSBSSS BSSSBBBB BBSSBBBB BSBSBBBB BSSSBBBB p  (q ^ r)  (p  q) ^ ( p  r)

4. Lat 9 hal 244 1.g BBBBSSSS BSBSBSBS BBSSBBSS BBSSBBSS BBBSBBBS SBSBSBSB BBBBSSSS BBBSBBBB BBSSBBBB BBBSBBBB p  (q v r)  ~r  ( p  q)

5. No.2 Rina bukan atlet lompat tinggi dan Rina bukan penari balet The Beatles bukan grup musik dari Inggris atau John L. tidak meninggal akibat penembakan Udin bukan seorang yang kikir atau Tia bukan seorang peragawati 2 3  8 atau 4 2  16 ada tamu negara dan polisi tidak bertugas di jalan protokol Ani naik kelas dan ia tidak dibelikan sepeda Tim tenis SMA Persada menang dan pemainnya tidak mendapat beasiswa dan tidak bebas SPP 2<5 dan 22  52

6. INVERS, KONVERS, KONTRAPOSISI B S B B B B S B B B S B B S B B  ~q  ~p ~p  ~q q  p p  q ~q ~p q p B B S S S B B S B S S B S S B B Kontraposisi invers konvers implikasi

7. CONTOH Konvers dari “Jika ada semut maka ada gula” Invers dari : p  (pVq) Kontraposisi dari : Jika ada guru tidak hadir maka semua murid bergembira Invers dari Jika semua siswa pintar maka semua guru senang. Invers dari konvers pernyataan: ~p  (p^q) Jika ada gula maka ada semut ~p  ~(pvq)  ~p  (~p^~q) Jika ada murid yang tidak bergembira maka semua guru hadir Jika ada siswa yang tidak pintar maka ada guru yang tidak senang ~(p^q)  p

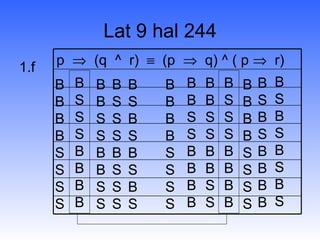
8. Penarikan kesimpulan: Modus ponens Premis 1 : p  q Premis 2 : p Kesimpulan  q Contoh : - Jika hari cerah saya pergi - hari cerah Kesimpulan : saya pergi B S B B B S S S B B B B S S S S S B S B B S B S B B B B [(p  q ) ^ p]  q

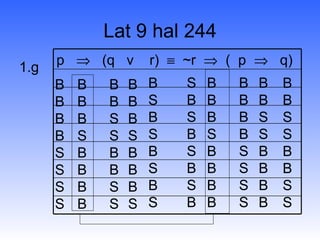
9. Modus Tolens Premis 1 : p  q Premis 2 : ~q Kesimpulan  ~p Contoh : - Jika hari cerah saya pergi - saya tidak pergi Kesimpulan : hari tidak cerah B S B B S S S B B B B B S S B B S B S B B S B S B B S S [(p  q ) ^ ~q ]  ~p

10. Silogisme Premis 1 : p  q Premis 2 : q  r Kesimpulan  p  r Contoh : - Jika hari cerah saya pergi - Jika saya pergi maka rumah kosong Kesimpulan : Jika hari cerah maka rumah kosong. - 1<2 - 2<3 Kesimpulan : 1<3

11. Apakah argumen berikut sah? ~p v q p  q p  q p ~r  ~q q  r  q  p  r ~r  ~p SAH SAH SAH

12. PR Lat 10 hal 245 no 1 Lat 12 hal 252 no. 11 no. 12, 13, 14,15,16,17,18