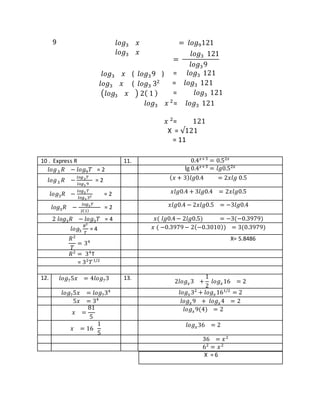
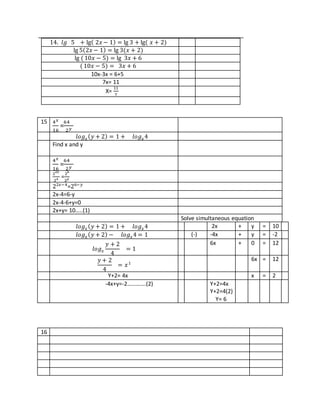
1. The document provides steps to solve various logarithmic equations. It expresses logarithmic equations in terms of logarithmic properties and solves for the unknown variables. 2. Several examples involve solving for logarithmic expressions equal to numbers or other logarithmic terms and isolating the unknown base or exponent. 3. Logarithmic properties like logab + logac = loga(bc) are used to transform equations into a form where the unknown can be extracted.

1. 1 log a p = x , log a q =y , log a = z
Find log a
𝑝2
𝑞
=log a
𝑝2
𝑞
=log a p2
– log a qr
=2x –( log a q + log a r )
=2x –( y + z )
=2x-y-z
2 Solve the equation 9 x
= 9 ( 3x
)-18
32x
= 32
(3x
) - 18
32x
= 32
(3x
) - 18
(3x
)2
= 32
(3x
) -18
Gantikan Y = 3x
Y2
= 9y - 18
Y2
= 9y +18=0
(y-3) ( y-6)=0
Y=3
3x
=3 3X
=6
X=1 log 10 3x
= log 10 6
x log 10 3 = log 10 6
X = log 10 6/ log 10 3 =1.631
3 Given a2
=p,
√𝑎=q
Log a
𝑝2𝑞
𝑎
Solution
a2
=p
log a a2
= log a p
2= log a p
√𝑎=q
a= q2
log a a= log a q 2
½ = log a q

2. Log a
𝑝2𝑞
𝑎
= log a p2
q – log a a
=( log a p2
+ log a q) - 1
=2 log a p + log a q -1
=2(2) + ½ - 1
=3 ½
4 log a2=m log a 3= n
log 6 24
= log a 24 / log a 6
= log a ( 23
x 3) / log a ( 2 x 3)
= log a 23
+ log a 3 / (log a 2 + log a 3)
= 3 m + n /( m + n)
5 Solve the equation 6. Log a (
𝑥3 𝑦4
𝑧
)
= (𝑙𝑜𝑔 𝑎 𝑥3
+ 𝑙𝑜𝑔 𝑎 𝑦4
) − 𝑙𝑜𝑔 𝑎 𝑧
= (3 𝑙𝑜𝑔𝑎 𝑥 + 4 𝑙𝑜𝑔 𝑎 𝑦 ) −
𝑙 𝑜𝑔 𝑎 𝑧
Log 10 x = 9 log x 10
Log 10 x = 9 log x 10
= 9 log 10 10
Log 10 x
7 Log 2 64
= log 2 26
= 6 log 22
= 6 (1)
(log 10 x) ( log 10 x ) = 9
(Log 10 x)2
= 9
Log 10 x = √9
= 3
x = 10 3
= 1000
8 Log 9 3
= Log 3 3/log 3 9
=1/ log 3 32
=1/2 (log 3 3)
=1/2 (1) =1/2

3. 9 𝑙𝑜𝑔3 𝑥 = 𝑙𝑜𝑔9121
𝑙𝑜𝑔3 𝑥
=
𝑙𝑜𝑔3 121
𝑙𝑜𝑔39
𝑙𝑜𝑔3 𝑥 ( 𝑙𝑜𝑔39 ) = 𝑙𝑜𝑔3 121
𝑙𝑜𝑔3 𝑥 ( 𝑙𝑜𝑔3 32 = 𝑙𝑜𝑔3 121
(𝑙𝑜𝑔3 𝑥 ) 2( 1 ) = 𝑙𝑜𝑔3 121
𝑙𝑜𝑔3 𝑥 2
= 𝑙𝑜𝑔3 121
𝑥 2
= 121
X = √121
= 11
10 . Express R 11. 0.4 𝑥+3
= 0.52𝑥
𝑙𝑜𝑔3 𝑅 − 𝑙𝑜𝑔9 𝑇 = 2 lg 0.4 𝑥+3
= 𝑙𝑔0.52𝑥
𝑙𝑜𝑔3 𝑅 −
𝑙𝑜𝑔3 𝑇
𝑙𝑜𝑔3 9
= 2 ( 𝑥 + 3) 𝑙𝑔0.4 = 2𝑥𝑙𝑔 0.5
𝑙𝑜𝑔3 𝑅 −
𝑙𝑜𝑔3 𝑇
𝑙𝑜𝑔3 32 = 2 𝑥𝑙𝑔0.4 + 3𝑙𝑔0.4 = 2𝑥𝑙𝑔0.5
𝑙𝑜𝑔3 𝑅 −
𝑙𝑜𝑔3 𝑇
2(1)
= 2 𝑥𝑙𝑔0.4 − 2𝑥𝑙𝑔0.5 = −3𝑙𝑔0.4
2 𝑙𝑜𝑔3 𝑅 − 𝑙𝑜𝑔3 𝑇 = 4 𝑥( 𝑙𝑔0.4− 2𝑙𝑔0.5) = −3(−0.3979)
𝑙𝑜𝑔3
𝑅2
𝑇
= 4 𝑥 ( −0.3979− 2(−0.3010)) = 3(0.3979)
𝑅2
𝑇
= 34
X= 5.8486
𝑅2
= 34
T
= 32
𝑇1/2
12. 𝑙𝑜𝑔75𝑥 = 4𝑙𝑜𝑔73 13.
2𝑙𝑜𝑔 𝑥3 +
1
2
𝑙𝑜𝑔 𝑥16 = 2
𝑙𝑜𝑔75𝑥 = 𝑙𝑜𝑔734 𝑙𝑜𝑔 𝑥32
+ 𝑙𝑜𝑔 𝑥161/2
= 2
5𝑥 = 34
𝑙𝑜𝑔 𝑥9 + 𝑙𝑜𝑔 𝑥4 = 2
𝑥 =
81
5
𝑙𝑜𝑔 𝑥9(4) = 2
𝑥 = 16
1
5
𝑙𝑜𝑔 𝑥36 = 2
36 = 𝑥2
62
= 𝑥2
X = 6

4. 14. 𝑙𝑔 5 + lg( 2𝑥 − 1) = lg 3 + lg( 𝑥 + 2)
lg 5(2𝑥 − 1) = lg 3(𝑥 + 2)
lg (10𝑥 − 5) = lg 3𝑥 + 6
( 10𝑥 − 5) = 3𝑥 + 6
10x-3x = 6+5
7x= 11
X=
11
7
15 4 𝑥
16
=
64
2 𝑦
𝑙𝑜𝑔 𝑥( 𝑦 + 2) = 1 + 𝑙𝑜𝑔 𝑥4
Find x and y
4 𝑥
16
=
64
2 𝑦
22𝑥
24 =
26
2 𝑦
22𝑥−4
=26−𝑦
2x-4=6-y
2x-4-6+y=0
2x+y= 10…..(1)
Solve simultaneous equation
𝑙𝑜𝑔 𝑥( 𝑦 + 2) = 1 + 𝑙𝑜𝑔 𝑥4 2x + y = 10
𝑙𝑜𝑔 𝑥( 𝑦 + 2) − 𝑙𝑜𝑔 𝑥4 = 1 (-) -4x + y = -2
𝑙𝑜𝑔 𝑥
𝑦 + 2
4
= 1
6x + 0 = 12
𝑦 + 2
4
= 𝑥1
6x = 12
Y+2= 4x x = 2
-4x+y=-2………….(2) Y+2=4x
Y+2=4(2)
Y= 6
16

5. 17 𝑙𝑜𝑔32 = 0.631 𝑙𝑜𝑔35 = 1.465
𝑙𝑜𝑔31.2 = 𝑙𝑜𝑔3
12
10
= 𝑙𝑜𝑔3
22
× 3
2 × 5
= 2𝑙𝑜𝑔32 + 𝑙𝑜𝑔33 − (𝑙𝑜𝑔32 + 𝑙𝑜𝑔35 )
= 2(0.631) +1 – (0.631 + 1.465)
=
18
𝑙𝑜𝑔3
25
4
= 𝑙𝑜𝑔3
52
22
=
2𝑙𝑜𝑔3 5
2𝑙𝑜𝑔3 2
=
2(1.465)
2(0.631)
=
19 𝑙𝑜𝑔5 √21 = 𝑙𝑜𝑔5 √3 × 7
= 𝑙𝑜𝑔53 × 71/2
1
2
𝑙𝑜𝑔5 ( 3 × 7)
1
2
(𝑙𝑜𝑔5 3 + 𝑙𝑜𝑔5 7)
=
20 2𝑙𝑜𝑔10(𝑥 − 𝑦) = 1 + 𝑙𝑜𝑔10 𝑥 + 𝑙𝑜𝑔10 𝑦
Proof 𝑥2
+ 𝑦2
= 12𝑥𝑦
𝑥2
+ 𝑦2
= 12𝑥𝑦
𝑙𝑜𝑔10(𝑥 − 𝑦)2
= 𝑙𝑜𝑔10 10 + 𝑙𝑜𝑔10 𝑥𝑦
𝑙𝑜𝑔10(𝑥 − 𝑦)2
− 𝑙𝑜𝑔1010 = 𝑙𝑜𝑔10 𝑥𝑦
(𝑥−𝑦)2
10
= xy
(𝑥 − 𝑦)2
= 10𝑥𝑦
( 𝑥 − 𝑦)( 𝑥 − 𝑦) = 10 xy
𝑥2
− 𝑥𝑦 − 𝑥𝑦 + 𝑦2
=10xy
𝑥2
+ 𝑦2
=12xy is proven