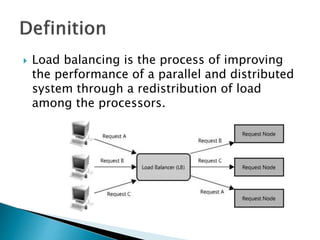
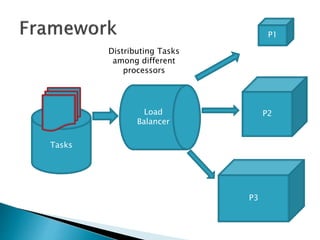
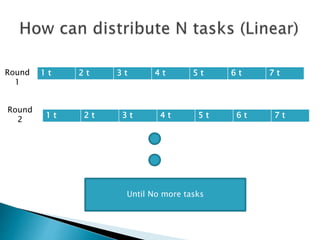
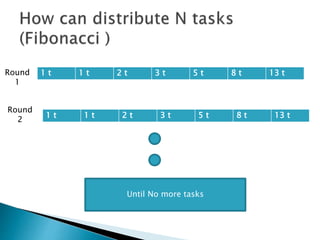
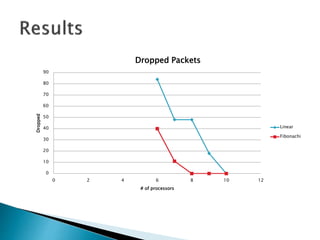
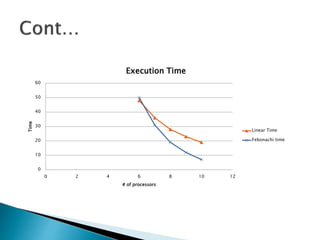
The document discusses load balancing techniques in distributed systems. It explains static and dynamic load balancing algorithms such as round robin, random, central manager, and threshold algorithms. Genetic algorithms and their application to load balancing problems are also covered. The performance of different load balancing strategies is evaluated based on metrics like execution time, dropped packets, and processor utilization. Specifically, the document finds that distributing load based on processor capabilities using a Fibonacci weighting scheme can maximize utilization of high-capability processors and minimize load on low-capability processors.

1. Omar Darwish

2.  Load balancing is the process of improving
the performance of a parallel and distributed
system through a redistribution of load
among the processors.

3. Who Initialized the load balancing algorithm ?
 Sender Initiated
◦ Initialized by the sender.
◦ Sender sends request messages till it finds a
receiver that can accept the load.
 Receiver Initiated
◦ Initiated by the receiver.
◦ Receiver sends request messages till it finds a
sender that can get the load.

4.  The performance of the processors is
determined at the beginning of execution.
 Master processor and slave processors.
 A task is always executed on the processor to
which it is assigned.
 Reduce the execution time, minimizing the
communication delays

5.  Round Robin Algorithm
◦ Processor choosing is performed in series and will
be back to the first processor if the last processor
has been reached.
 Randomized Algorithm
◦ Uses random numbers to choose slave processors
based on statistics .

6.  Central Manager Algorithm
◦ The central processor is able to gather all slave
processors load information
◦ The chosen slave processor is the processor having
the least load
 Threshold Algorithm
◦ The processes are assigned immediately upon
creation to hosts.
◦ Under loaded, medium and overloaded.

7.  Dynamic algorithms allocate processes
dynamically when one of the processors
becomes under loaded.
 Buffered in the queue
 Allocated dynamically upon requests from
remote hosts

8.  Central Queue
◦ Stores new activities and unfulfilled requests as a
cyclic FIFO queue on the main host.
 Local Queue
 A parameter defines the minimal number of
ready processes the load manager attempts
to provide on each processor

9.  Adaptability
◦ Static No, Dynamic Yes
 Predictability
◦ Static Yes, Dynamic No
 Waiting Time (Queuing time )
 Execution System

10.  Fitness Function
◦ The main objective of GA is to find a schedule with
optimal cost while load-balancing.
 Less execution time.
 Less communication cost.
 Higher processor utilization.
 Maximum system throughput

11.  Selection
 Processors permutation
 Crossover
 Exchange portions between strings.
 Mutation
 Change the genes in a chromosome
(Processors set)

12.  NP complete problem.
 Untractable with large N of tasks and P
number of processors.

13. Actual execution cost
If we consider communication time, the work
load L is

14.  Objective function

16.  Processor 1  3 tasks/slot
 Processor 2 6 tasks/slot
 GCD =3
 P1 P0 P1 P1 P0 P1 P1 P0 P1
O(n log log n/log n),
GCD in parallel

17.  Static Algorithms
 Round robin fashion
 Heterogeneous processors
 Weighting processors depends on capabilities
 Fibonacci gives the high capabilities
processors extra load.

18.  Rank processors depends on capabilities
 Give each processor weight depends on its
rank (linearly or Fibonacci)
 While (process<>0)
◦ Assign tasks for each processor depends on its
weight

19.  Linear approach
 Ex
◦ Ordering weights (1,2…,7)
◦ 7 processors
◦ The highest capability takes weight 7
◦ The lowest capability takes weight 1
◦ Processor 7 will get 7 process each slot time
◦ Processor 1will get 1 process each slot time

20.  Fibonacci approach
 Ex
◦ Ordering weights (1,1,2,3,5,8,13)
◦ 7 processors
◦ The highest capability takes weight 13
◦ The lowest capability takes weight 1
 Processor 7 will get 13 process each slot time
 Processor 1will get 1 process each slot time

21. Load
Balancer
Tasks
P1
P2
P3
Distributing Tasks
among different
processors

22. 1 t 2 t 3 t 4 t 5 t 6 t 7 t
Round
1
1 t 2 t 3 t 4 t 5 t 6 t 7 t
Round
2
Until No more tasks

23. 1 t 1 t 2 t 3 t 5 t 8 t 13 t
Round
1
1 t 1 t 2 t 3 t 5 t 8 t 13 t
Round
2
Until No more tasks

24.  M tasks
 K processors
 How to distribute tasks among the processors
 Less drops packets
 Less time

25.  Number of processors N 6,7,8,9,10
 Processors speed :
◦ High speeds (N/2) =0.10 * i  i is the processor #
◦ Low speeds (N/2) =0.03 * i  i is the processor #
 For example processor with id 6 can process
6.0*0.10*number of tasks in the Queue
 Processor with id 2 can process 2.0*0.3*number of tasks in
the Queue .
 Memory
For High speed computers 20 * i locations
For low speed computers 320*i locations
 1000 tasks
 Arrival packets =20, 33,….

26. 0
10
20
30
40
50
60
70
80
90
0 2 4 6 8 10 12
Dropped
# of processors
Dropped Packets
Linear
Fibonachi

27. 0
10
20
30
40
50
60
0 2 4 6 8 10 12
Time
# of processors
Execution Time
Linear Time
Febonachi time

28.  Fibonacci distribution guarantee the more
utilization of higher capabilities processors
and less load on the less capabilities
processors.

29.  The presentation explore:
◦ Static vs. Dynamic load balancing technique.
◦ The formulization of task scheduling problem.

30.  Sharma, Sandeep, Sarabjit Singh, and Meenakshi Sharma. "Performance analysis of
load balancing algorithms." World Academy of Science, Engineering and
Technology 38 (2008): 269-272.
 Rajguru, Abhijit A., and S. S. Apte. "A Comparative Performance Analysis of Load
Balancing Algorithms in Distributed System using Qualitative
Parameters." International Journal of Recent Technology and Engineering 1.3
(2012).
 Shah, Purnima, and S. M. Shah. "Load Balancing in Distributed System Using
Genetic Algorithm}." Special issues on IP Multimedia Communications}: 139-142.
 Attiya, Gamal, and Yskandar Hamam. "Task allocation for minimizing programs
completion time in multicomputer systems." Computational Science and Its
Applications–ICCSA 2004. Springer Berlin Heidelberg, 2004. 97-106.
 Chor, Benny, and Oded Goldreich. "An improved parallel algorithm for integer
GCD." Algorithmica 5.1-4 (1990): 1-10.
 http://kb.linuxvirtualserver.org/wiki/Weighted_Round-Robin_Scheduling

31. Questions ?