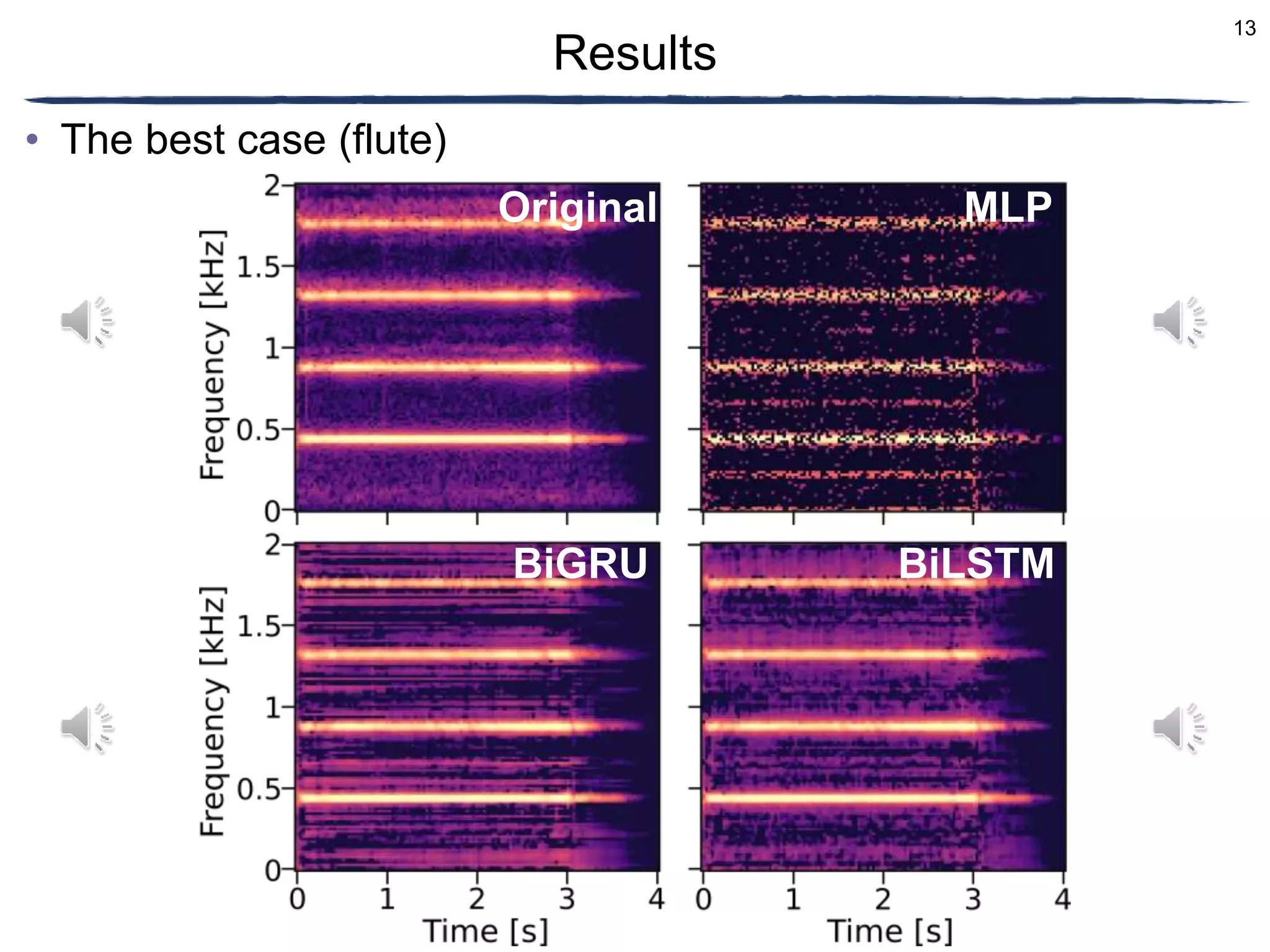
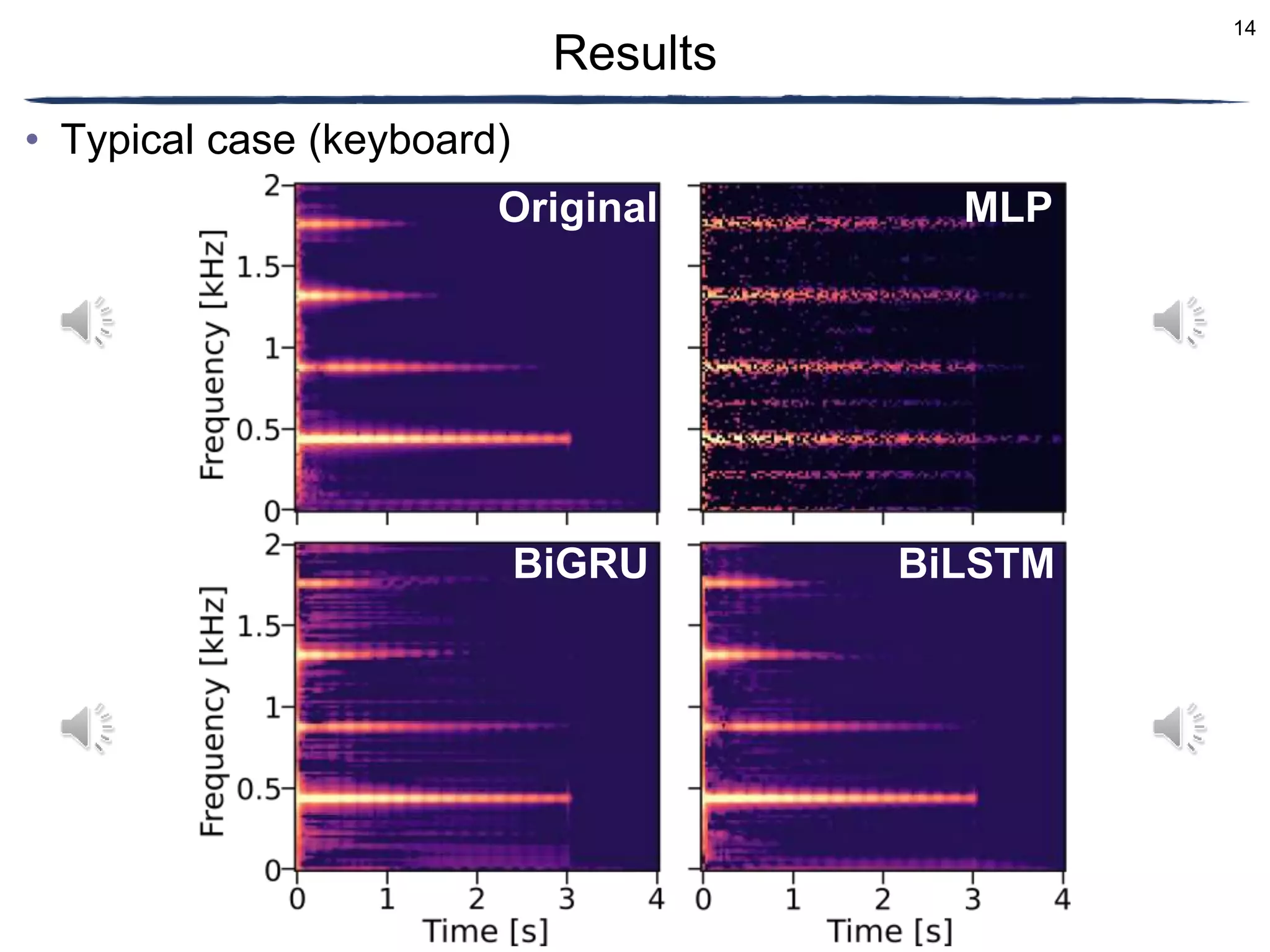
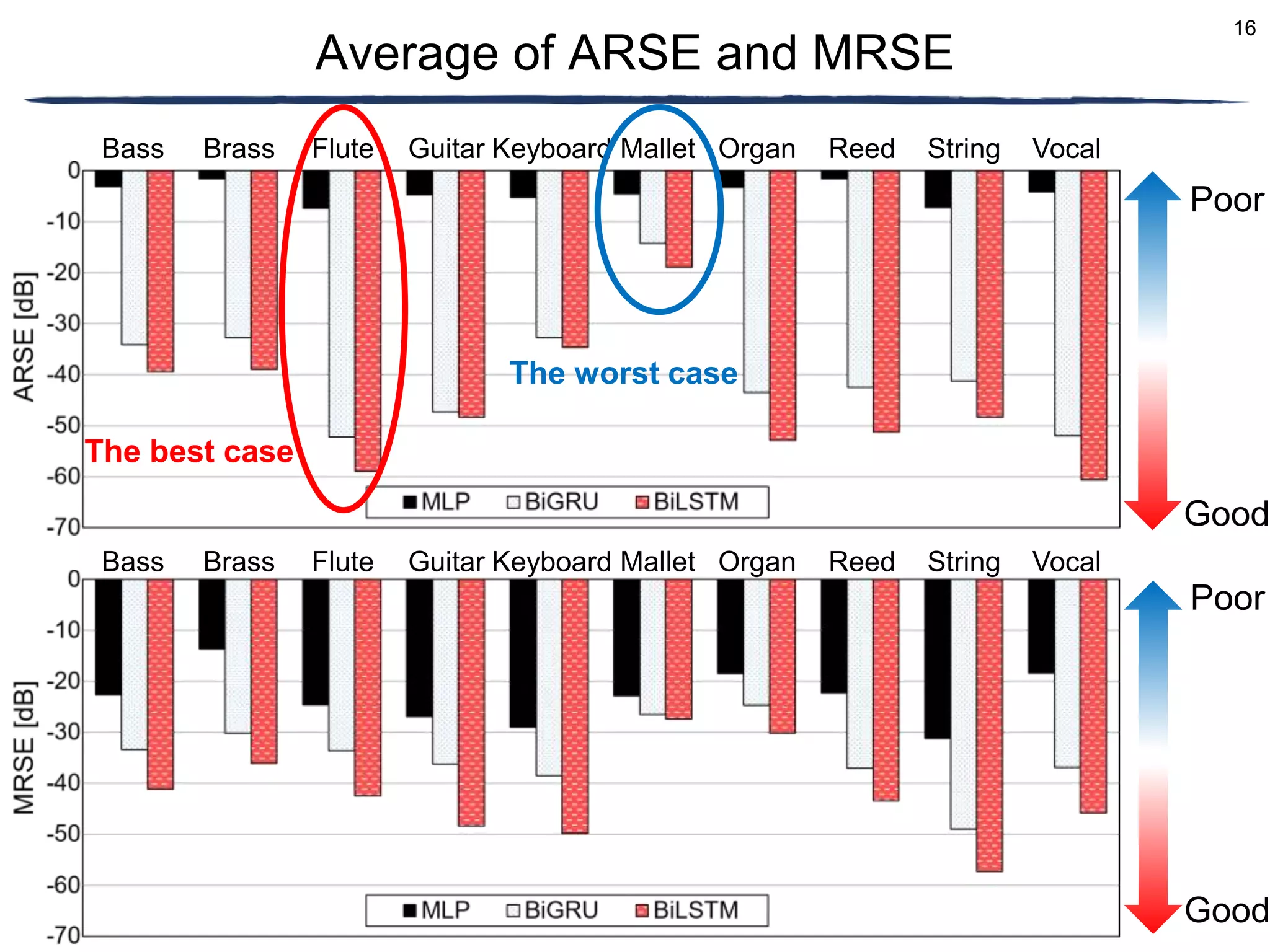
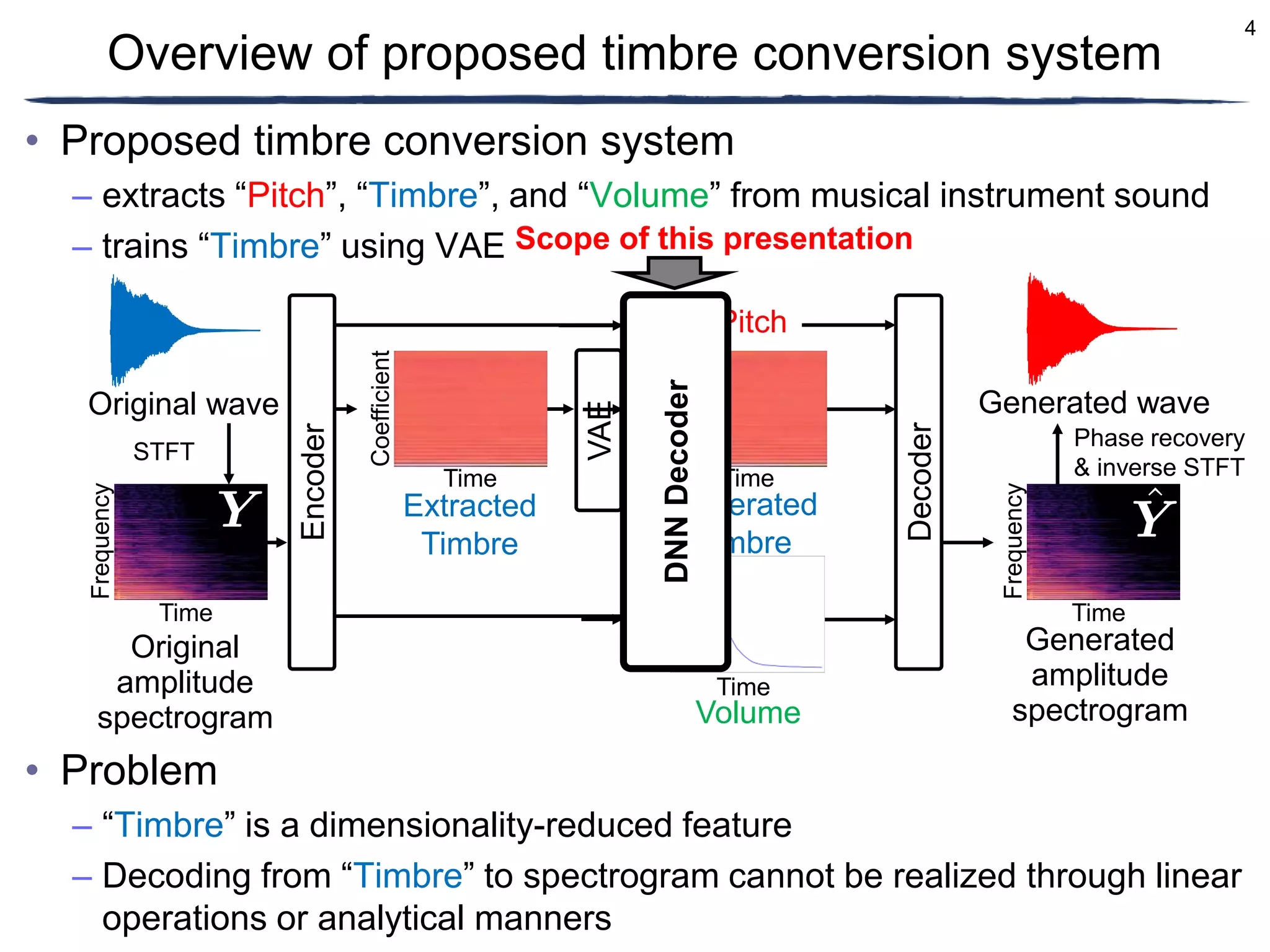
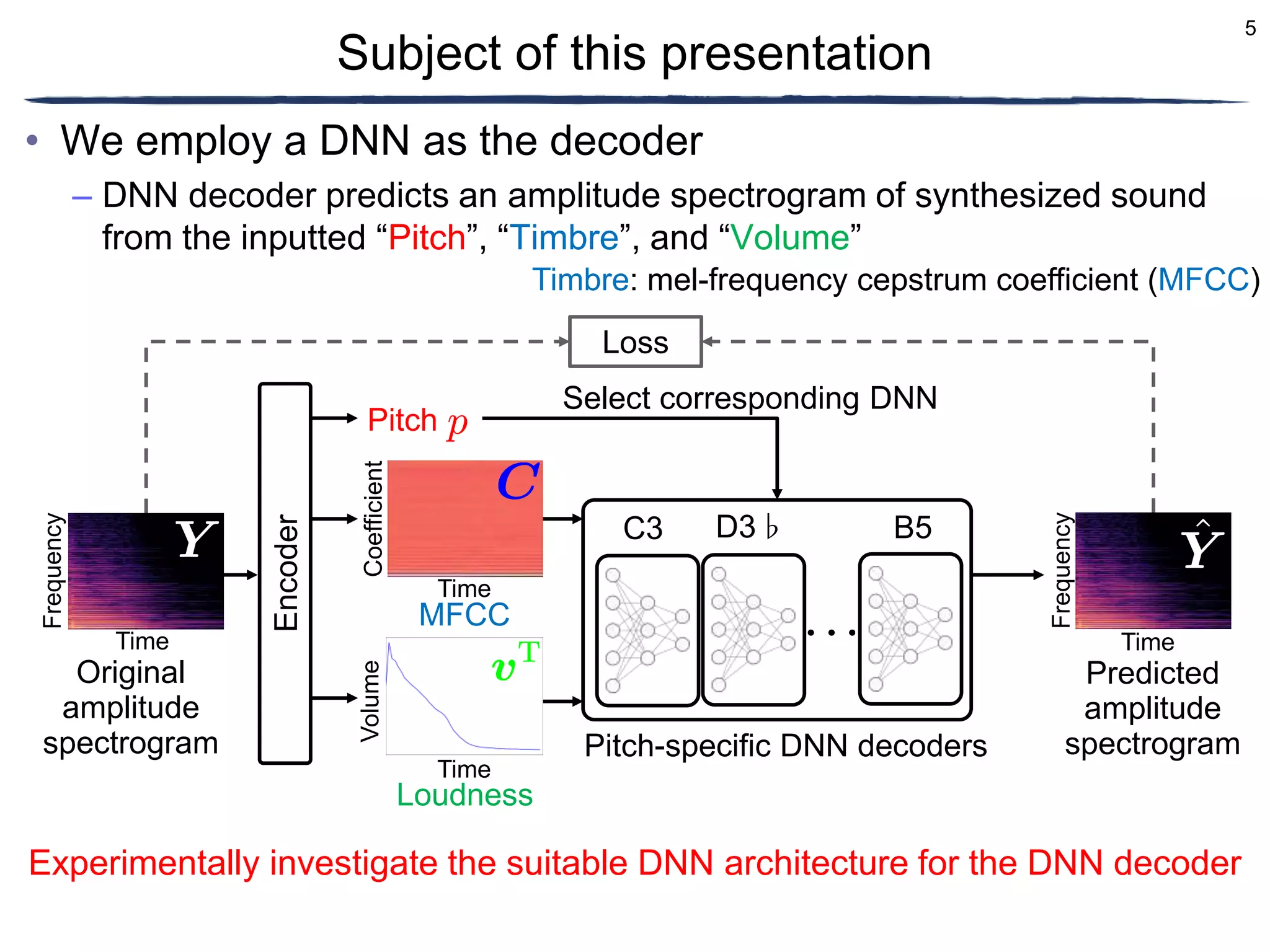
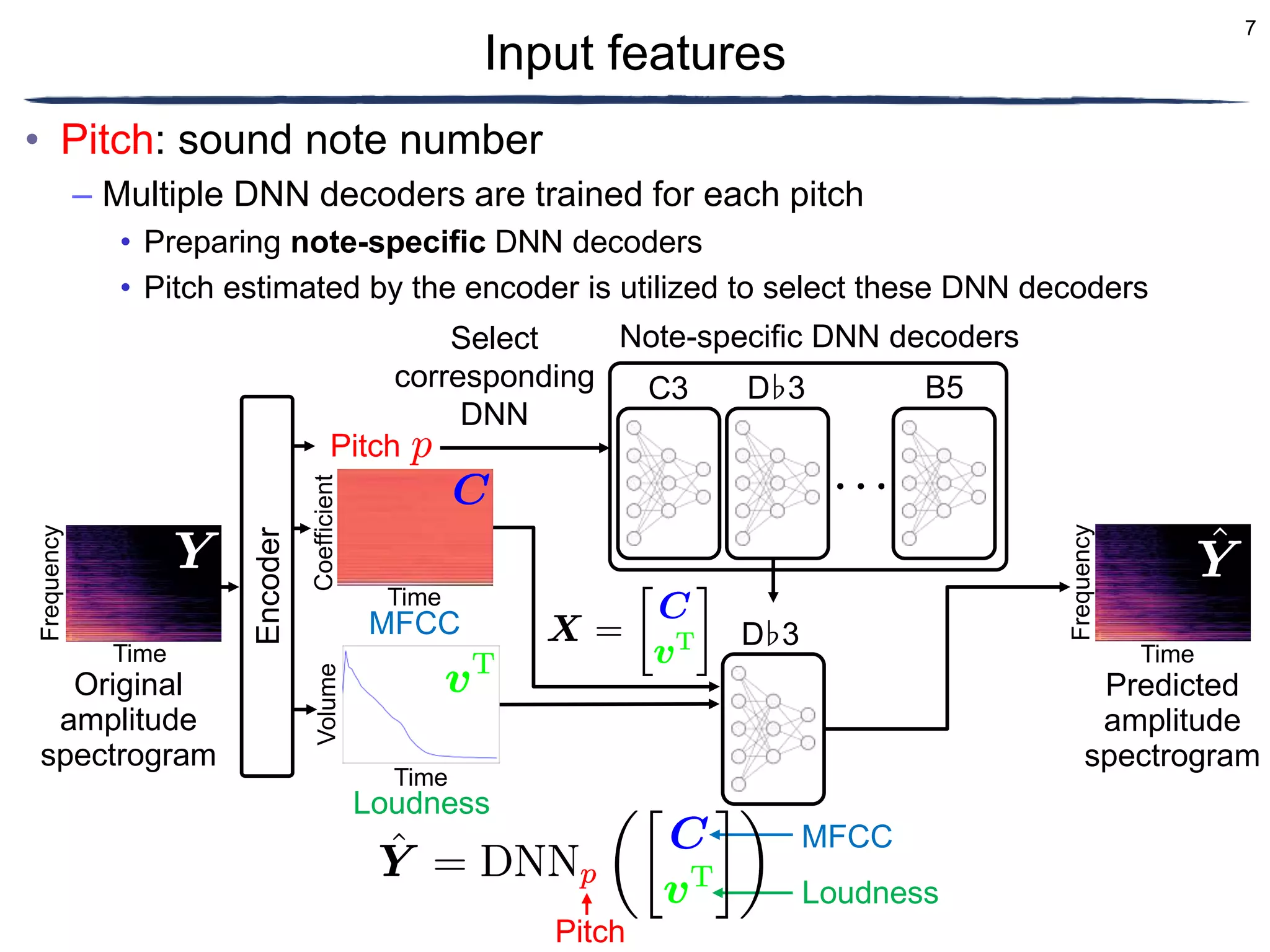
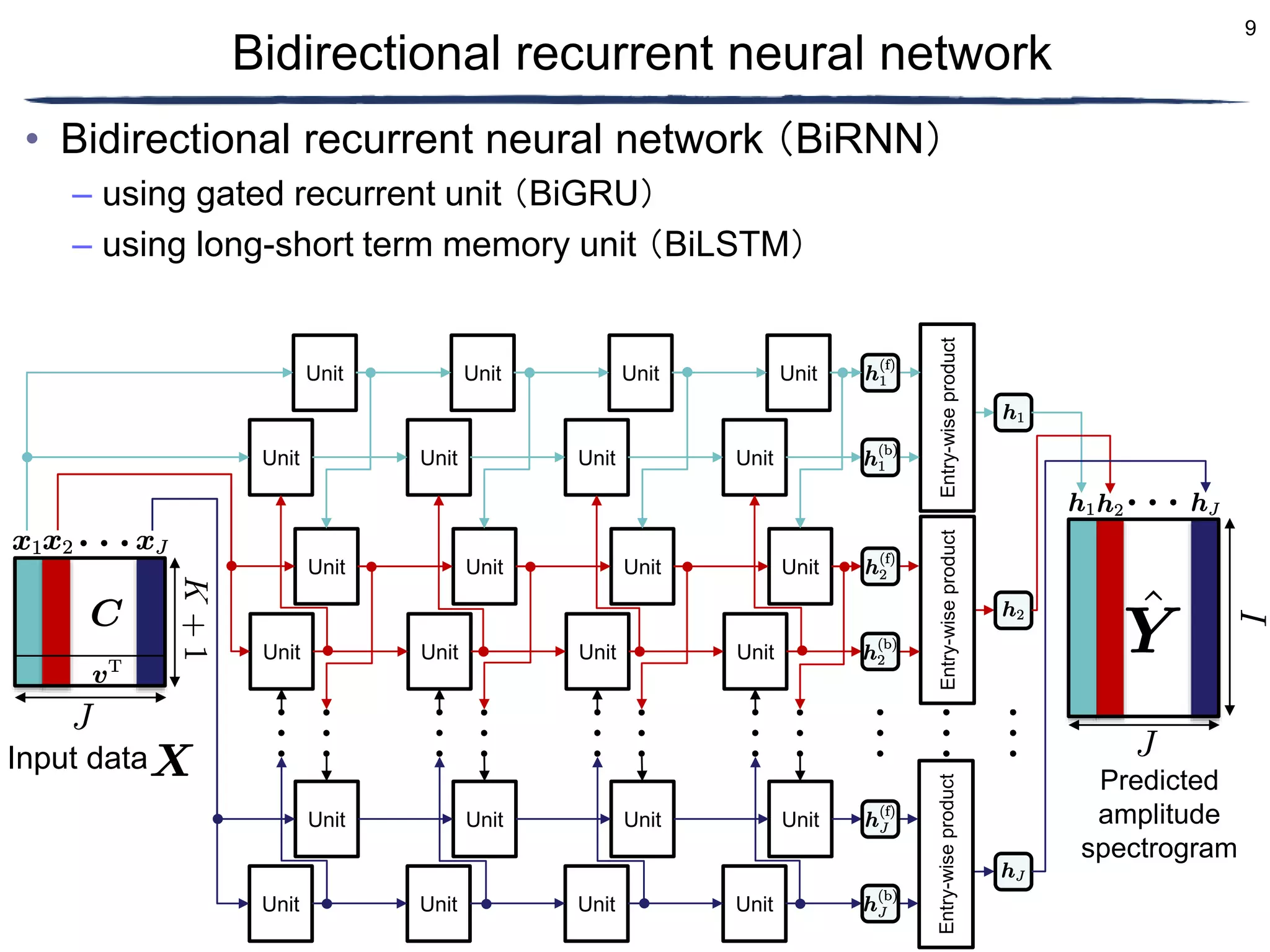
The document discusses a proposed timbre conversion system that utilizes deep neural networks (DNN) to predict amplitude spectrograms from mel-frequency cepstrum coefficients (MFCC) and loudness. It highlights the architecture of the system, including the use of variational auto-encoders (VAE) and different DNN architectures such as multilayer perceptrons and bidirectional recurrent neural networks. Results indicate that the use of a bi-directional long short-term memory (BiLSTM) decoder can effectively predict amplitude spectrograms with high accuracy.

![2
Background
• Timbre conversion of musical instrument sounds
– Differentiable Digital Signal Processing (DDSP) [Engel+, 2020]
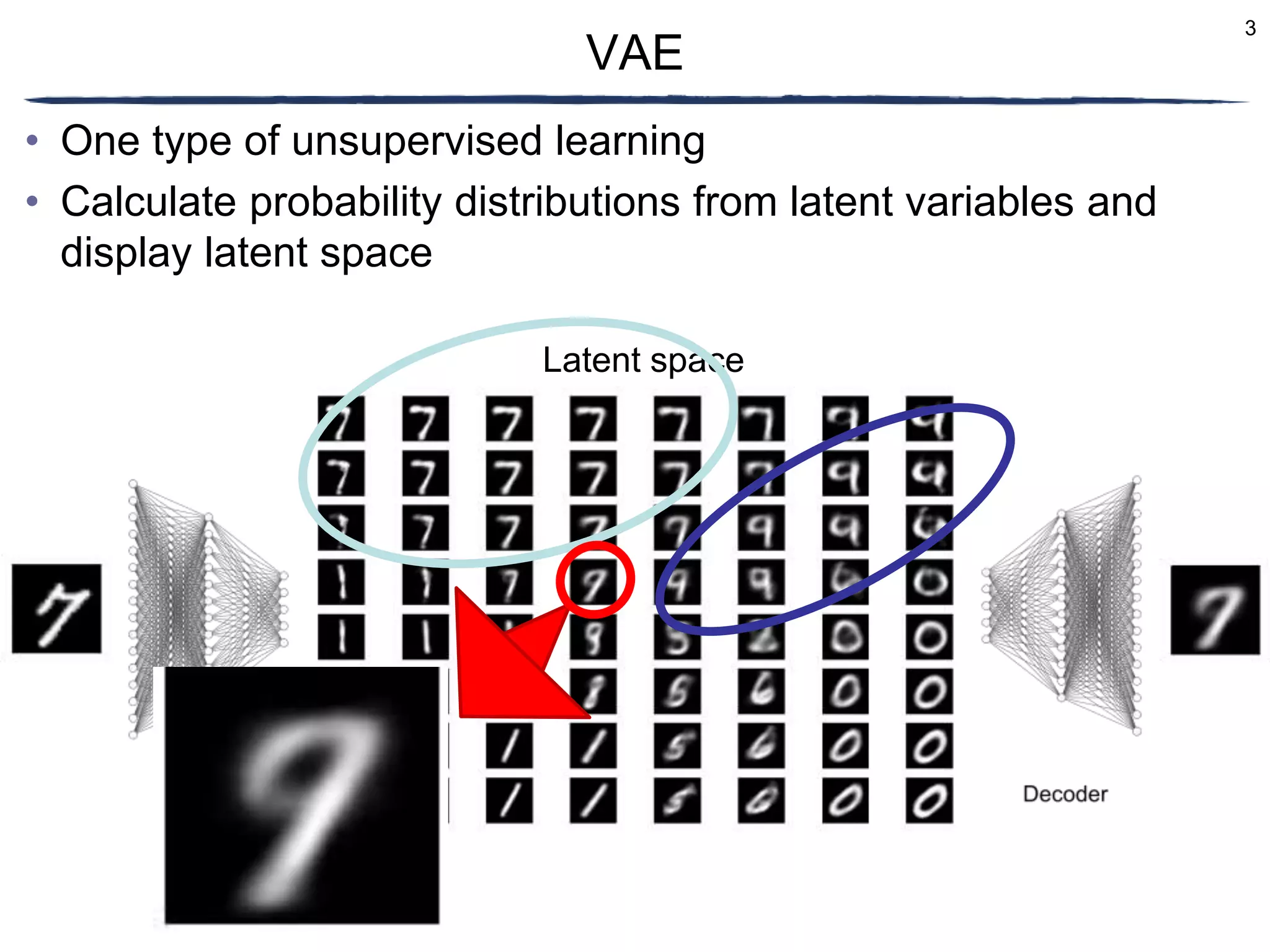
– Generation of musical instrument sounds using variational auto-encoder
(VAE) [Luo+, 2019]
• Conversion of timbre and generation of musical instrument
sound using VAE [Kingma+, 2013]
– Timbre intermediate between piano and guitar
– New musical instrument sound
Conversion
Existing music Converted music
Conversion](https://image.slidesharecdn.com/ncspkawaguchifinal-230302022452-9e3ab004/75/Amplitude-spectrogram-prediction-from-mel-frequency-cepstrum-coefficients-and-loudness-using-deep-neural-networks-2-2048.jpg)
![6
• Volume: loudness
– Feature of time-frame-wise sound volume
• Timbre: mel-frequency cepstrum coefficient (MFCC)
– Legacy timbre features
Input features
MFCC
Amplitude spectrogram
Time [s]
Frequency
[kHz]
Time [s]
Coefficient
Loudness
Time [s] Time [s]
Frequency
[kHz]
Volume
Amplitude spectrogram Frequency
[kHz]
Normalized amplitude spectrogram
Time [s]
Frequency bin:
Time frame:
Mel-filter bank
and DCT](https://image.slidesharecdn.com/ncspkawaguchifinal-230302022452-9e3ab004/75/Amplitude-spectrogram-prediction-from-mel-frequency-cepstrum-coefficients-and-loudness-using-deep-neural-networks-6-2048.jpg)

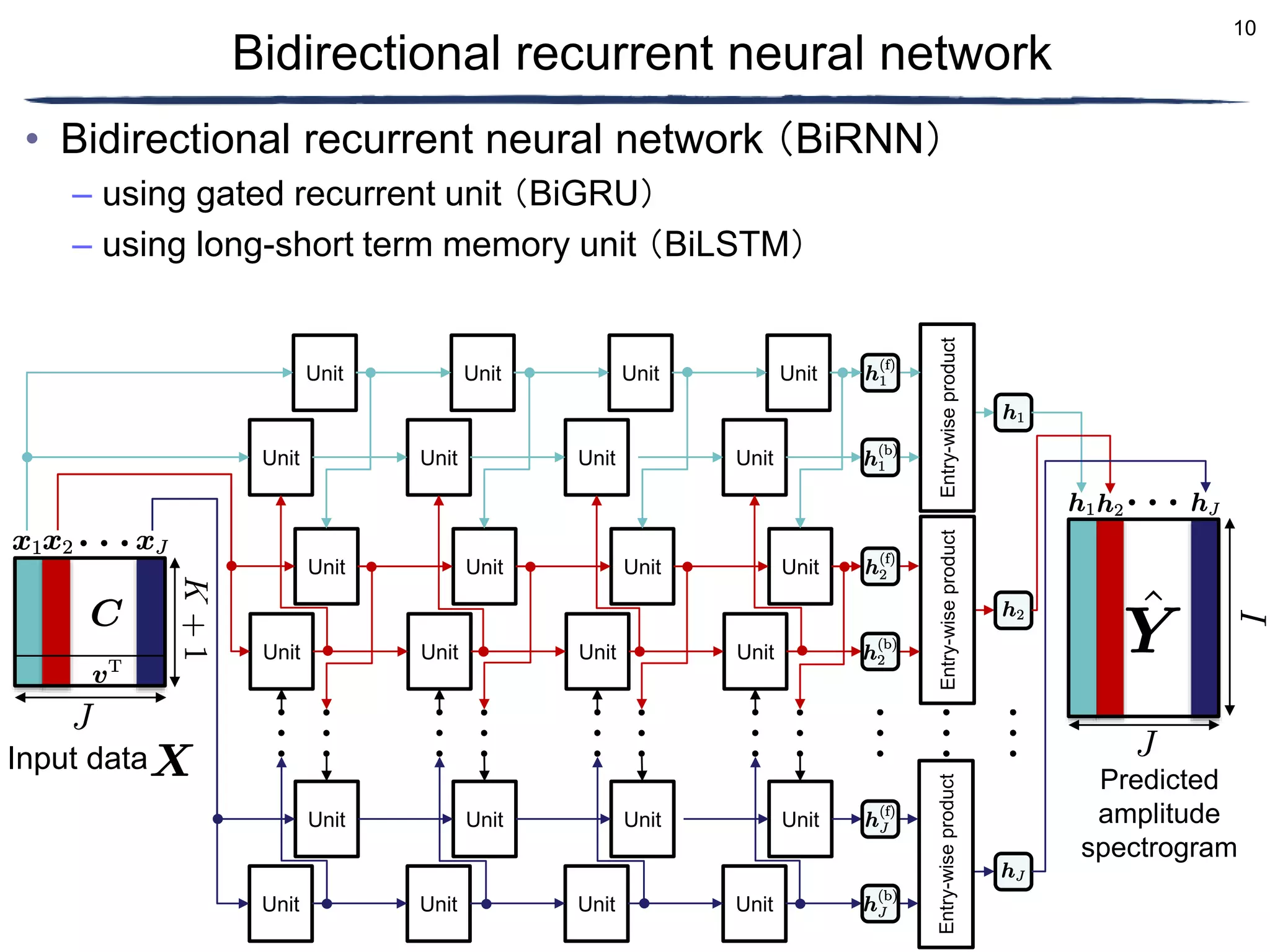
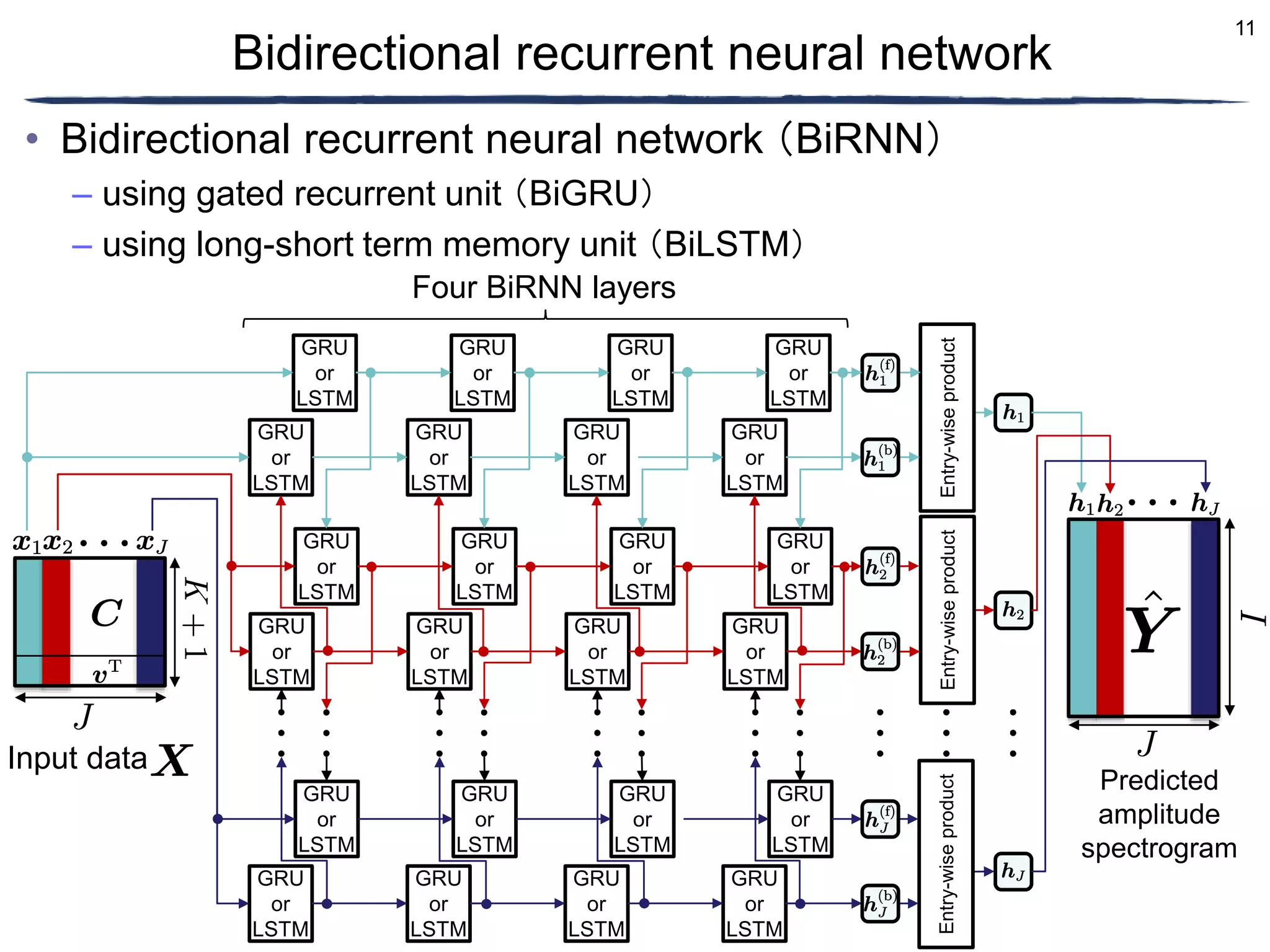
![12
• Dataset of musical instruments: Nsynth [Engel+, 2017]
– 305,979 signals of four-second-long various musical instrumental sounds
with 16 kHz sampling frequency
– was split into 289,205 (95%) training, 12,678 (4%) validation, and
4,096 (1%) test data
• Other conditions
Condition
Window and shift lengths in STFT 64 / 32 ms
Window function in STFT Hann window
Number of epochs 10000
Maximum frequency of mel filter bank 8.00 kHz
Minimum frequency of mel filter bank 0.00 kHz
Number of mel filters ( ) 64
Loss function Mean squared error](https://image.slidesharecdn.com/ncspkawaguchifinal-230302022452-9e3ab004/75/Amplitude-spectrogram-prediction-from-mel-frequency-cepstrum-coefficients-and-loudness-using-deep-neural-networks-12-2048.jpg)