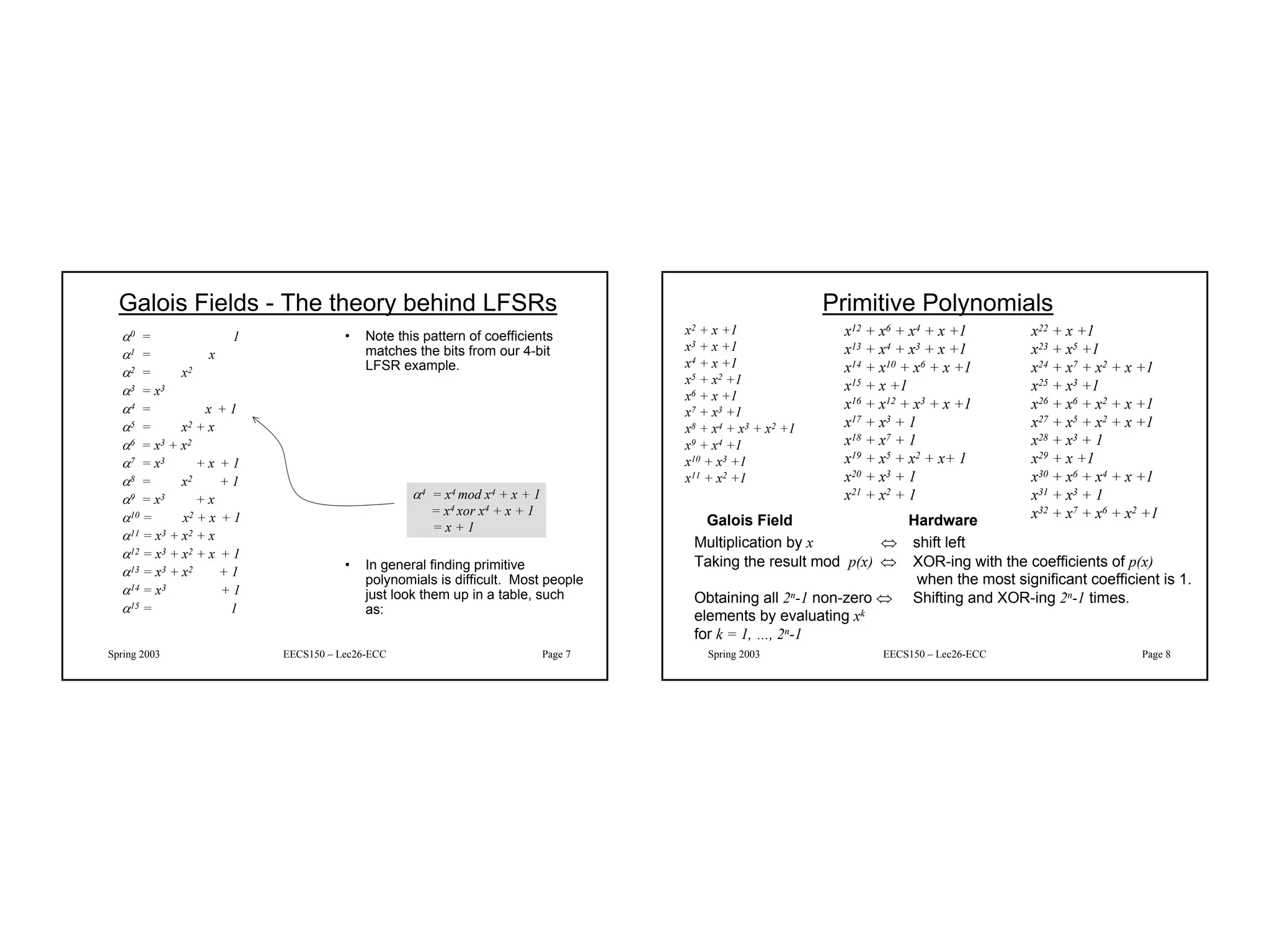
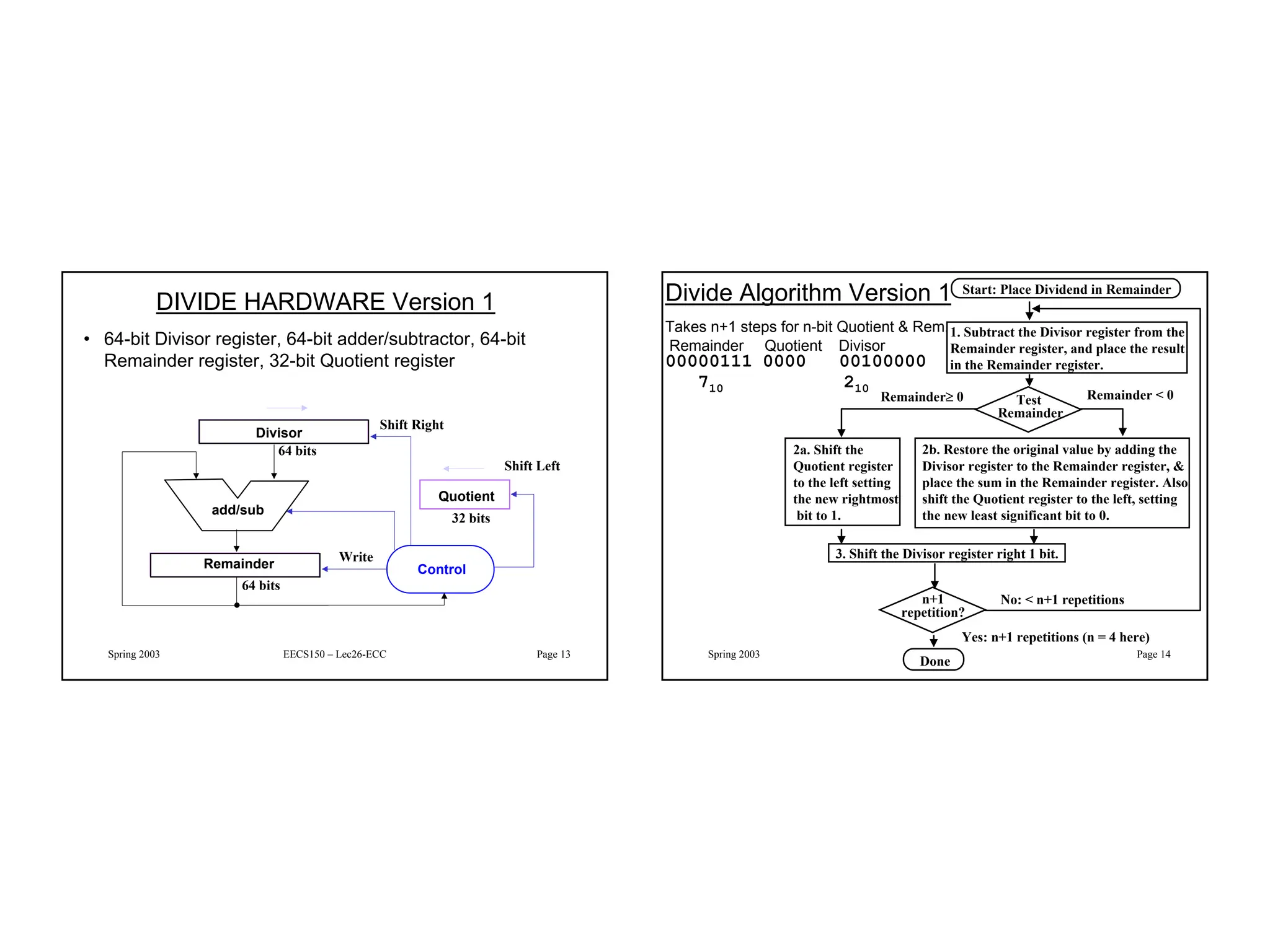
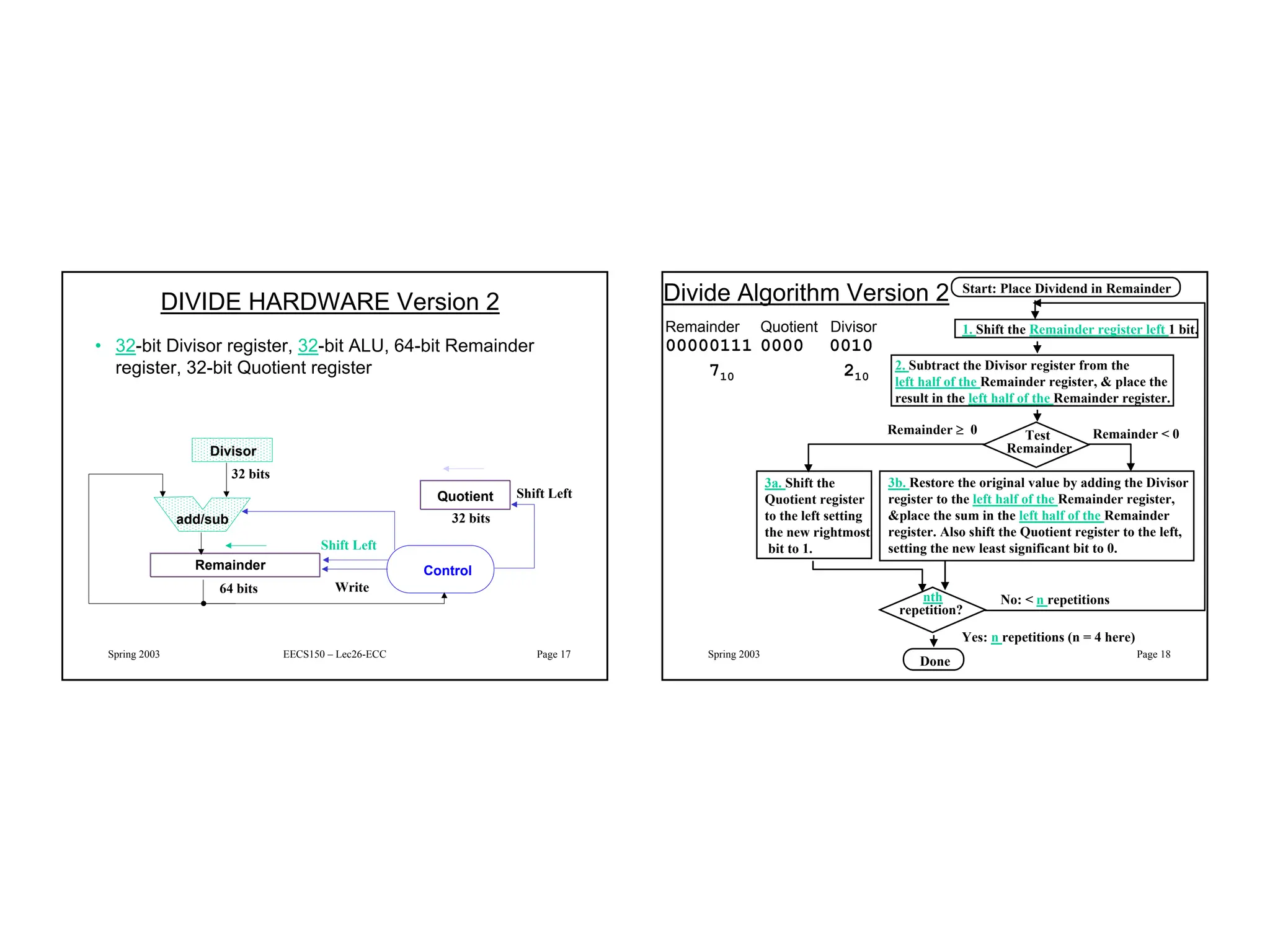
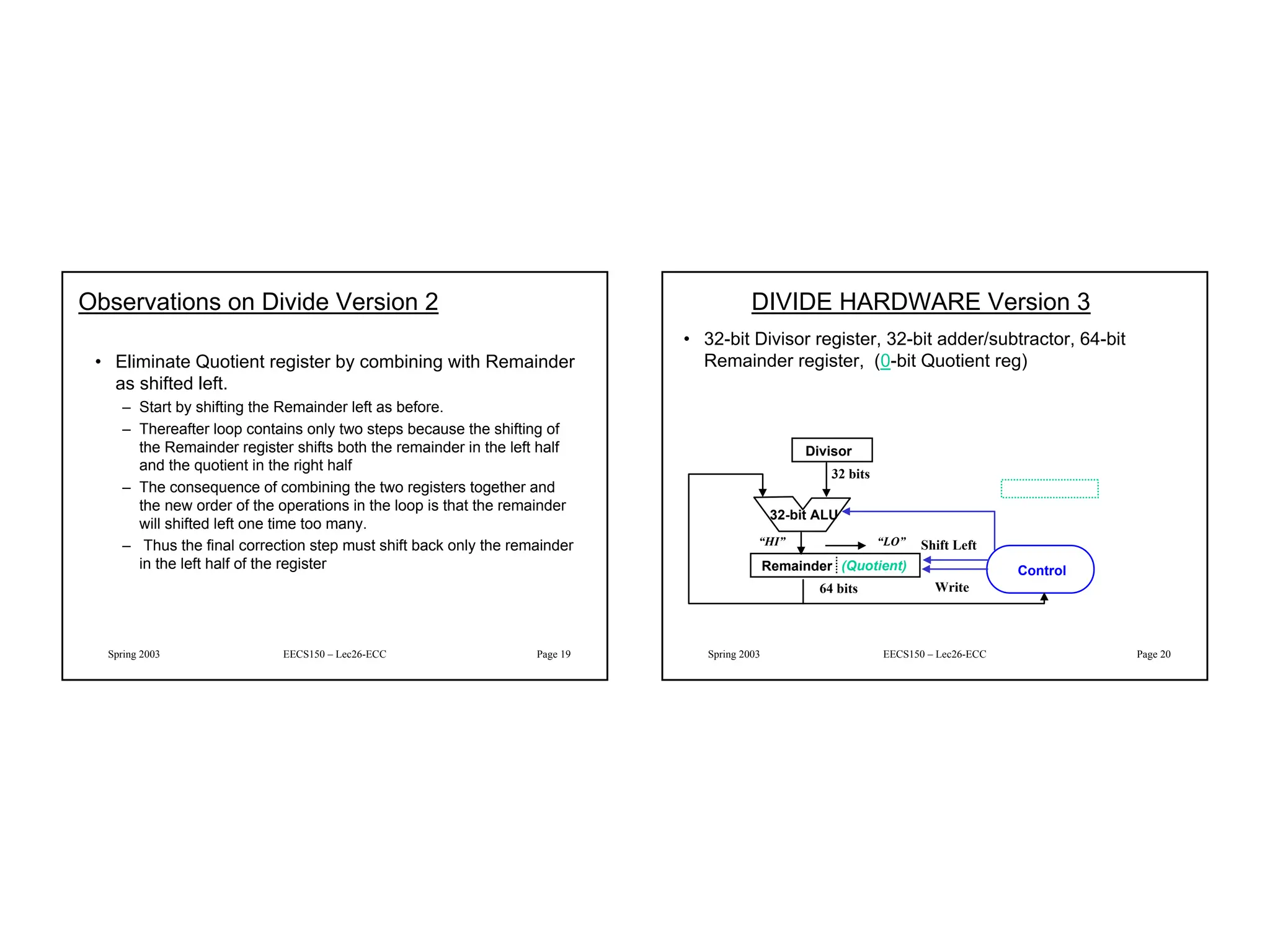
Linear feedback shift registers (LFSRs) are circuits that can generate pseudo-random sequences of bits. They consist of a shift register with XOR logic gates in a feedback path. LFSRs can be used for random number generation, error detection and correction codes, and counting applications. They are efficient in that they require little hardware and operate at high speeds. The document then provides examples of 4-bit and 8-bit LFSR circuits and discusses how LFSRs can implement finite field arithmetic over Galois fields using polynomial representations. It also describes how LFSRs can be used to generate parity bits for error detection codes.