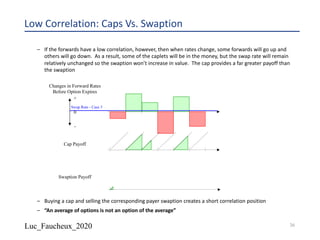
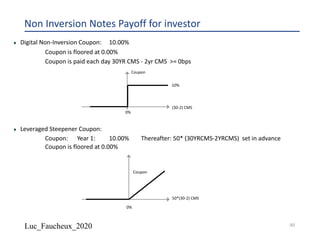
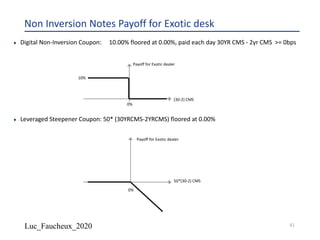
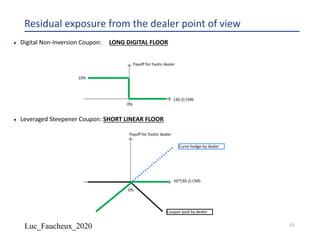
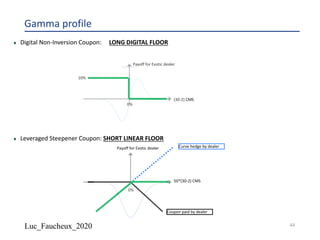
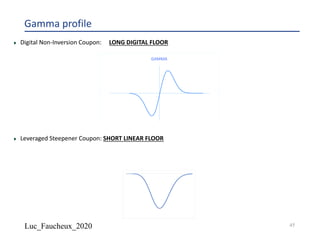
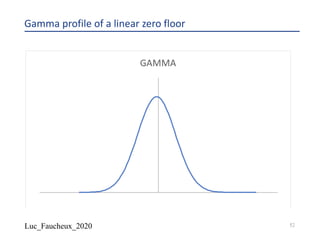
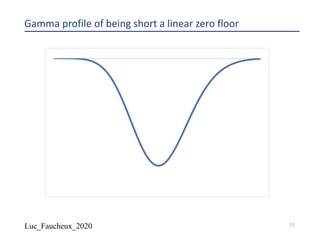
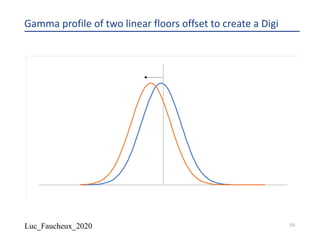
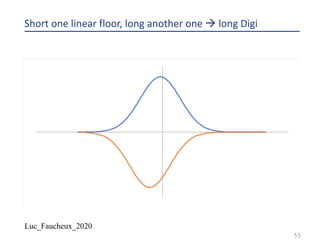
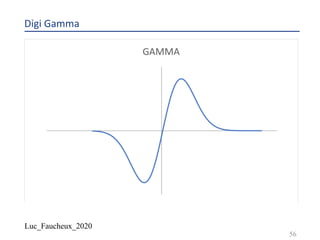
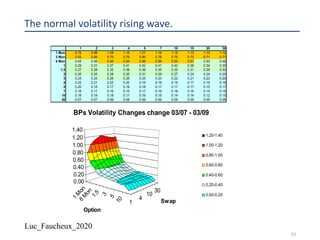
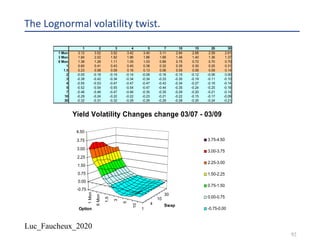
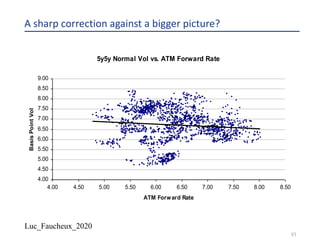
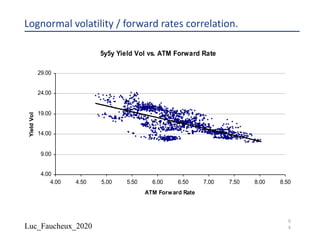
The document provides a comprehensive overview of structured products, defining them as financial instruments designed to meet specific investor needs through customized features. It discusses various types of structured products, their issuance process, investor demographics, risks, and benefits, as well as specific examples like callable notes and range accruals. The popularity of structured products stems from their ability to enhance yields while offering investors access to unique market opportunities.

1. Luc_Faucheux_2020
Introduction to Structured Products
Examples and impact on the Vanilla market
through dynamic hedging
1

2. Luc_Faucheux_2020
Overview
¨ Structured Notes market
¨ Common notes
¨ How the structured notes market drive the curve, the non-inversion notes
¨ How the structured market drive the volatility, the callable notes
2

3. Luc_Faucheux_2020
What is a Structured Product?
A Structured Product is a financial instrument designed to meet specific investor needs by
incorporating special, non-standard features including:
Tax Efficiency:
At times, long-term
capital gains
Transparency:
Formula based
payoffs and
secondary markets
Fee Efficiency:
Compared
to alternatives
Enhanced
Returns:
Leveraged
participation in
upside
Alpha Generation
Time Horizon:
Tailored to
investors’
preferences
Access:
To new markets in
an efficient manner
Downside
Protection:
Partial or full
capital protection
3

4. Luc_Faucheux_2020
Different Forms of Structured Products
Structured returns may be embedded in either a note or a swap, or ETF
¨ Investor pays an upfront fee in return for a note
that pays structured coupon and is redeemed at
par
Note
¨ One party pays a structured coupon and receives
a floating rate in return
Swap
Investor
Issuer
Structured Coupon
+
Par at Maturity
Party A Party BUpfront Fee
Structured Coupon
Floating Rate
+/-
Spread
Question: Besides investment banks and other sophisticated financial institutions who have the
ability to risk manage a structured payout, who would want to issue structured notes?
4

5. Luc_Faucheux_2020
Issuance Process
Answer: Any corporation may issue structured notes! If the issuer does not want to take on the structured
risk, which most often is the case, then they may enter into an offsetting swap. As a result, the issuer
effectively sells a floating rate note
¨ Example: XYZ Corporation issues $250mm of notes paying a structured coupon
– First, XYZ issues the notes to investors in exchange for an upfront payment
– Then, XYZ enters into a swap with the street to convert its structured obligation into a standard floating rate payment stream
Street Issuer XYZ
Structured Coupon
Floating Rate
+/-
Spread
Investor
Structured Coupon
+
Par at Maturity
Upfront Fee
– XYZ’s payment profile is exactly that of a vanilla floating rate note
¨ Why, then, would XYZ opt to issue structured notes instead of vanilla floating rate notes or other debt obligations?
¨ Simple: Structured notes can provide issuers with funding at levels better than those that may be achieved through vanilla
bonds
– For example, if a particular structured note is in high demand relative to standard floating rate notes, then issuers may obtain
cheaper funding (i.e. at a lower spread to LIBOR) by issuing that structured note and swapping the exotic risk into a floating rate,
rather than issuing floaters directly
5

6. Luc_Faucheux_2020
Interest Rate Structured Note Market
¨ The interest rate structured note market is still quite large
¨ In H1 2008, Lehman Brothers had underwritten the highest volume in interest rate linked structured
notes, with over 20% market share at the time and 3bn notional
6

7. Luc_Faucheux_2020
Home Loan Banks and FHLMC GSEs
7

8. Luc_Faucheux_2020
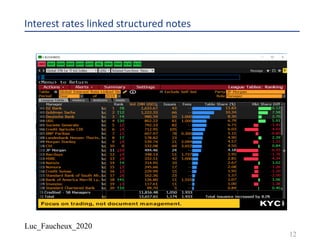
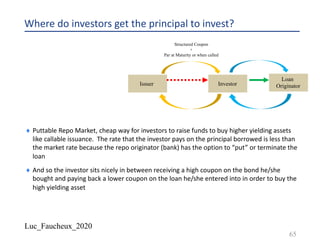
FHLMC 2.5 03/21/2025 [Corp][GO]
8

9. Luc_Faucheux_2020
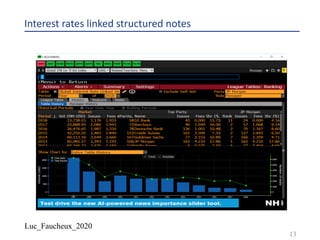
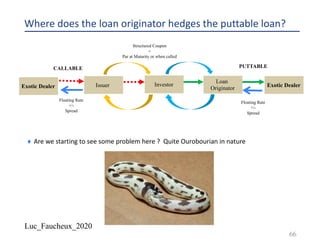
FHLMC 2.5 03/21/2025 [Corp][GO]{call}
9

10. Luc_Faucheux_2020
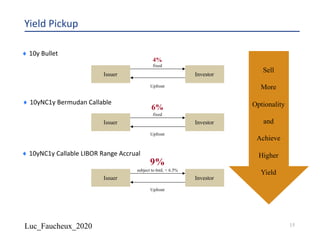
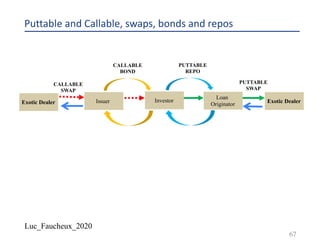
FHLMC 2.5 03/21/2025 [Corp][GO]{Coupon}
10

11. Luc_Faucheux_2020
Global issuance Structured Notes
11
Because of the leverage and the associated risk, notional size can be deceiving

12. Luc_Faucheux_2020
Interest rates linked structured notes
12

13. Luc_Faucheux_2020
Interest rates linked structured notes
13

14. Luc_Faucheux_2020
Why is the Structured Notes Market so Large?
Structured notes are fully customizable, and a primary reason for their popularity is that they enable
investors to achieve yield enhancement by selling optionality
¨ In most structured notes, the investor effectively buys a vanilla note and writes options to the issuer. The option premium is reflected
in a higher note coupon
¨ Simple Example: 10yNC1y Bermudan Callable (“10 Year No-Call 1 Year”)
– Note pays a fixed coupon, but the issuer may call it, or redeem it at par, after 1 year and semi-annually thereafter
– Compared to a 10y bullet (a note which is not callable), the 10yNC1y will pay a higher fixed rate since the noteholder has sold the option to
cancel the trade
¨ Another Example: 10yNC1y Callable LIBOR Range Accrual
– Investor receives a fixed coupon multiplied by the fraction of days during the period on which a specified LIBOR rate is within a certain range
– For example, the investor could receive a semi-annual coupon of 9% x (N / D), where
– N is the number of days in each semi-annual period on which six-month LIBOR is below 6.5%, and
– D is the total number of days in the semi-annual period
– Note is complex, but will pay a higher fixed rate than the 10yNC1y Bermudan Callable since the investor has sold more optionality
– Digital cap with daily looks on six-month LIBOR, struck at the upper range boundary (6.5% in this case)
– Bermudan call option on the combination of the fixed coupon and digital cap, struck at par
14

15. Luc_Faucheux_2020
Yield Pickup
¨ 10y Bullet
Issuer Investor
4%
fixed
Upfront
¨ 10yNC1y Bermudan Callable
Issuer Investor
6%
fixed
Upfront
¨ 10yNC1y Callable LIBOR Range Accrual
Issuer Investor
9%
subject to 6mL < 6.5%
Upfront
Sell
More
Optionality
and
Achieve
Higher
Yield
15

16. Luc_Faucheux_2020
Investors
Typical investors are institutional accounts and retail/high net worth individuals
¨ Main types of investors
– Institutional
– Banks
– Asset managers
– Insurance companies
– Pension funds
– Non-Institutional
– High net worth
– Retail
¨ The level of sophistication varies between
investor types and geographies
Types of Investors
Institutional
¨ The objective of institutional investors is often to
monetize a view on the market they wouldn’t
otherwise be able to take
– E.g., A European bank wants to take a view on the
USD curve but without taking exposure to the
EUR/USD currency risk
Non-Institutional
¨ Often want to get yield enhancement (i.e. an
above market return) through speculation on a
view
– E.g., the 10 year USD swap rate will remain at least
100 basis points above the 2 year USD swap rate
Investor Objectives
16

17. Luc_Faucheux_2020
Typical Structures
17

18. Luc_Faucheux_2020
Common Interest Rate-Linked Structures
Structures have been developed that enable investors to monetize a wide range of views
¨ Focus: Yield Levels
– Callable LIBOR Range Accrual – Realized LIBOR rates will rise slower than forward curve implies
– CMS Countdown, Snowball – Realized yield curve will be lower, or fall more quickly, than the forward curve implies
– Snowbear – Realized yield curve will be higher, or rise faster, than the forward curve implies
¨ Focus: Yield Curve Shape
– CMS Spread Callable Note – Magnitude of steepening will be greater than forward curve implies
– CMS Spread Callable Range Accrual – Likelihood of steepening differs from what the forward curve implies
– CMS Spread Target Redemption Note – Timing of steepening will differ from what the forward curve implies
¨ Focus: Volatility Surface
– Callable Bond – Realized volatility will be lower than what volatility surface implies
Structure View
18

19. Luc_Faucheux_2020
Callable Range Accrual : the most frequent structure
– Full name: Callable Daily Range Accrual Note (CDRAN)
– Bermudan call option held by the issuer
– Daily coupon accrual if reference rate within range
– Senior unsecured debt – 100% of principal paid at redemption or maturity
– Coupon payout – above market coupon if reference rate within range, otherwise 0%
– Similar concept to selling out-of-the-money interest rate cap
– Investor collects a premium and loses money if LIBOR goes above the strike,
– Except range notes have limited downside and above market coupon instead of upfront
premium
6mL
Coupon
6%
7.00%
6mL0
Payoff
6%
19

20. Luc_Faucheux_2020
Range Note2
– Reference rate can be any point on the swaps curve: 3mL, 6mL, 2y CMS, 10y CMS, etc.
– CMS = Constant Maturity Swap: 10y CMS is the 10y swap rate on any given day at 11AM
– Short-term rates are most popular because they are tied to monetary policy
– If your view is the Fed won’t hike rates dramatically => range condition will be satisfied and full
coupon will be paid
– Range boundary is dependent on investor’s risk appetite
– The tighter the range, the higher the coupon
– In last 15yrs, 3mL was between (0-7) 100% of the time; (0-6.5): 95%; (0-6): 91%; (0-5.5): 76%
3mL Forward Curve
0.00%
1.00%
2.00%
3.00%
4.00%
5.00%
6.00%
7.00%
8.00%
1Y 5Y 15Y10Y
Historical 3mL
0.00%
1.00%
2.00%
3.00%
4.00%
5.00%
6.00%
7.00%
8.00%
Jun-96
Jun-97
Jun-98
Jun-99
Jun-00
Jun-01
Jun-02
Jun-03
Jun-04
Jun-05
Jun-06
Jun-07
Jun-08
Jun-09
Jun-10
Jun-11
20

21. Luc_Faucheux_2020
Range Note3
– Structures are highly customizable
– Bearish structures: Y1: 6.50% fixed, Y2-15: 6.50% subject to 10y CMS >= 4.00%
– Floating rate structures: 3mL + 250 subject to (0-7) range on 3mL
– Step up structures:
– Y1-5: 6.25% subject to (0-5) range on 6mL
– Y6-10: 6.50% subject to (0-5.5) range on 6mL
– Y11-15: 7.00% subject to (0-6) range on 6mL
– Longer term reference rates tend to result in higher coupons due to forward curves
– Most common reference in the US is 6mL because of a slight pick up to 3mL
Forward Curves
0.00%
1.00%
2.00%
3.00%
4.00%
5.00%
6.00%
3m 6m 2y 10y
1Y 5Y 10Y 15Y
21

22. Luc_Faucheux_2020
Who Issues Range Notes?
– US Agencies and Financial Institutions
– Federal Home Loan Banks (FHLB) – Aaa/AAA
– Federal Home Loan Mortgage Corp (FHLMC) – Aaa/AAA
– International Bank for Reconstruction and Development (IBRD) – Aaa/AAA
– Swedish Export Credit (SEK) – Aa1/AA+
– Eksportfinans – Aa1, AA
– Toyota Motor Credit Corp (coming soon) – Aa2/AA-
– UBS AG – Aa3, A+
– Lloyds TSB Bank PLC – Aa3, A+
– Issuance declined after the financial crisis
0
1
2
3
4
$Billions
2008 2009 2010 2011*
* - 2011 annualized
Issuer USD(M) Eqv No. MTNs %
1 FEDERAL HOME LOAN BANKS 725 29 54.2
2
FEDERAL HOME LOAN MORTGAGE
CORP
250 3 18.7
3 BARCLAYS BANK PLC 223 12 16.7
4 ROYAL BANK OF CANADA 60 2 4.5
5 Others 80 7 6.0
Total 1,338 53 100.0
Dealer USD(M) Eqv No. MTNs %
1 Barclays Capital Group 578 21 43.2
2 Morgan Stanley 271 4 20.3
3 UBS 150 5 11.2
4 Nomura 64 7 4.8
5 Others 275 16 20.6
Total 1,338 53 100.0
22

23. Luc_Faucheux_2020
Who Issues Range Notes?
– Issuance Process
– Issuer enters into a swap with Exotic Options desk to avoid paying high coupon
– Net result for the issuer – floating rate debt at attractive funding level
– Issuer is exposed to the credit risk of swap counterparty but Investor is only exposed to Issuer’s
credit
– Issuer guarantees coupon and principal payments of the note
– Call decision is usually driven by the underlying swap
– If Exotics desk calls the swap, Issuer will likely call the notes (but is not required to)
+ the option to
call the swap
Exotic Options
Desk
Issuer Investor
Structured Coupon Structured Coupon
+ Par at Maturity
Floating Rate
+/- Spread
+ the option to
call the notes
Par at Issuance
23

24. Luc_Faucheux_2020
Risks
– Credit
– Coupons and principal are subject to the creditworthiness of the issuer
– In the event of default, investor receives same recovery value as all other senior unsecured creditors
– Interest Rates
– Like most bonds, as interest rates go up, price goes down
– Worst case scenario: range condition broken for the life of the note = zero coupon bond
– Interest Rate Volatility
– Investor is selling optionality – as volatility goes up, price goes down
– Reinvestment
– Issuer can call the note at par, returning the principal for reinvestment at market rates
– Extension
– A typical 15y NC 3m Range Note has a duration around 7yrs
– If reference becomes more likely to break the range, call probability goes down, duration extends
– Liquidity
– Range Notes are less liquid than vanilla bonds – wider bid/offer spreads
– Some dealers provide active secondary markets but not all dealers do
24

25. Luc_Faucheux_2020
Benefits
– Yield Enhancement
– 15y bullet: 4.75%
– 15y NC 6m Bermudan Callable: 5.25%
– 15y NC 6m (0-6%) Range Note: 7.00%
– Access to interest rate options market
– Very difficult for individuals to get an ISDA
– Call and Reinvest Strategy
– The expectation is that forwards will be realized and bond will be called after a few years
– Investor then rolls into a new issue
– The downside risk is if rates spike and the bond is not called
– Call Statistics (in a market rally, also observe the decrease in new deals)
– 2007 deals: 239/249 called (96%)
– 2008 deals: 177/183 called (97%)
– 2009 deals: 125/130 called (96%)
– 2010 deals: 57/80 called (71%)
Sell More Optionality,
Achieve Higher Yield
25

26. Luc_Faucheux_2020
Variations
– CMS Spread Range Accrual (CMS = Constant Maturity Swap)
– Coupon accrues if spread between 2 points on the swaps curve remains within range
– Most common structure pays if the yield curve remains positively sloped => Non-Inversion Note
– e.g. (30y CMS – 2y CMS) >= 0
– Dual Range Accrual
– Coupons accrues if 2 different conditions are both satisfied
– e.g. (0-7) on 3mL AND (30y CMS – 2y CMS) >= 0
– Investor is making a bet that the conditions are positively correlated
– If short-term rates stay low, the yield curve is not likely to invert
– Hybrid Range Accrual
– A form of dual range accrual that combines options from 2 different asset classes
– e.g. (0-7) on 3mL AND S&P 500 >= 80% of value at issuance
– For equity-linked structures, investor is selling equity vol, which is much higher than rates vol,
resulting in higher coupons
– Investors can combine conservative views on currencies, commodities, rates, or equities in order
to enhance yield
26

27. Luc_Faucheux_2020
Pricing & Hedging: The Basics
2
7

28. Luc_Faucheux_2020
Valuing and Hedging Structured Payouts
¨ Structured products contain a variety of complex options which, in general, are not easy to hedge; removing exotic risk is
like hedging apples with oranges
– Digital options on the difference between two underlyings, potentially involving multiple currencies and different asset classes
– Contingent options: Exercising one option cancels other options
– Options on options
¨ Although no perfect hedge exists for most exotic products, dealers can look at the primary risks involved in a particular trade
to determine (i) which are desirable, (ii) which will be hedged and (iii) which should be hedged but would be too expensive
to take off
– For example, in a CMS Spread Callable Range Accrual swap, the dealer is long digital caps and/or floors on the difference between
two swap rates, and is also long the option to sell the same digitals. Additionally, the dealer bears risk similar to that of a vanilla
Bermudan callable
– An exotics desk could sell vanilla Bermudan callables as a partial hedge, but would likely pay substantial bid/offer to do so. The desk
could also use European swaptions, but as a result would have a less effective hedge for the complex risk
– Likewise, trading digital caps and floors on the difference between two swap results would require paying significant transaction
costs. As an alternative, dealers may use linear caps and floors, or simply put on curve steepeners and flatteners using swaps or
even Treasurys, but the hedge will not be perfect
¨ A thorough understanding of option principles and financial mathematics is necessary to understand the complex risks in
exotics and how to hedge them efficiently.
After developing structures with attractive risk/reward profiles, dealers must be able to value and manage
the exotic risk they enter as a result of swapping note issuance
28

29. Luc_Faucheux_2020
Additional Risk Factors: Skew and Smile
¨ Black-Scholes assumes that volatility is constant
¨ In reality, volatility changes as the underlying moves. In the world of interest rates, volatility is negatively correlated with
the level of rates
– When interest rates are falling, normally the economy is entering into a rough period, economic growth is slowing and recession is a
concern. As a result of the uncertainty and fear, volatility tends to rise
– Likewise, when rates are rising, the Fed may be hiking to counter the inflationary effects of a prosperous economy, economic
growth is strong, etc. Due to the relative stability, volatility tends to fall
¨ Skew/Smile: How the implied volatility used to price an option varies with the strike of the option
– Generally speaking, options with lower strikes will trade at prices reflecting higher implied volatilities
– Volatility tends to be higher when low strike options are close to becoming in the money, making the option more valuable
– Analogously, options with higher strikes will trade with lower implied volatility
Moneyness (K – ATMF)
σ(K) (Lognormal Yield Vol)
29

30. Luc_Faucheux_2020
Additional Risk Factors: Vanna and Volga
¨ Vanna
– Sensitivity of Delta to changes in volatility
– Sensitivity of Vega to changes in the underlying
¨ Volga
– Sensitivity of Vega to changes in volatility
σV
(Option)
V
(Vega)
σ
(Delta)
Vanna
2
¶¶
¶
=
¶
¶
=
¶
¶
=
2
2
σ
(Option)
σ
(Vega)
Volga
¶
¶
=
¶
¶
=
K
Vanna
K
Volga
V
V
30

31. Luc_Faucheux_2020
Additional Risk Factors: Correlation
¨ When an option has multiple underlying assets, the correlation between the underlyings plays a key role
in the option’s price
¨ Example: 1-year call option on the difference between the 10 year swap rate and the 2 year swap rate
– Payoff = max(10Y swap rate – 2Y swap rate – K, 0)
– When pricing this option, the volatility of the spread between the two swap rates is relevant
– But, the volatility of the spread depends on the volatilities of the individual swap rates and the correlation
between the two rates:
σ2
10Y – 2Y = σ2
10Y + σ2
2Y - 2σ10Yσ2Yρ10Y, 2Y
– Since σ10Y and σ2Y are positive, the spread’s volatility, and as a result the value of the option, increases as the
correlation decreases
– Being long an option on the difference between two rates means you are short correlation
– Intuition: The less that the rates move in tandem, the more likely that the difference between the rates will
change
¨ CMS Spread Callable Notes and CMS Spread Callable Range Accruals bear this correlation risk, but are
even harder to hedge due to the callability
31

32. Luc_Faucheux_2020
Spread Option Vega buckets
¨ 𝑆 = 𝑋! − 𝑋"
¨ 𝛿𝑆 = 𝛿𝑋! − 𝛿𝑋"
¨ (𝛿𝑆)"= (𝛿𝑋! − 𝛿𝑋")"= 𝛿𝑋!
"
+ 𝛿𝑋"
"
− 2 𝛿𝑋! 𝛿𝑋"
¨ (𝛿𝑆)"~𝜎" 𝛿𝑡
¨ (𝛿𝑋!)"~𝜎!
" 𝛿𝑡
¨ (𝛿𝑋")"~𝜎"
" 𝛿𝑡
¨ (𝛿𝑋! 𝛿𝑋")~𝜌𝜎! 𝜎" 𝛿𝑡
¨ 𝜎" = 𝜎!
" + 𝜎!
" − 2𝜌𝜎! 𝜎"
32

33. Luc_Faucheux_2020
Spread option Vega buckets
¨ Partial Vegas for option
¨ Spread Vega:
#$
#%
¨ Bucketted Vegas:
#$
#%!
and
#$
#%"
¨
#$
#%!
=
#$
#%
.
#%
#%!
¨
#$
#%!
=
#$
#%
2(𝜎! − 𝜌𝜎")
¨
#$
#%"
=
#$
#%
2(𝜎" − 𝜌𝜎!)
33

34. Luc_Faucheux_2020
Bucketted Vega spread
¨
#$
#%!
=
#$
#%
2(𝜎! − 𝜌𝜎")
#$
#%"
=
#$
#%
2(𝜎" − 𝜌𝜎!)
¨ If 𝜎! > 𝜎": since the correlation in absolute value is always lower than 1
¨ The Vega to the most volatile asset has always the same sign as the Vega of the option to the
spread
¨ If the two assets are negatively correlated, the Vega to each assets has always the same sign
as the Vega to the spread
¨ If the two assets are positively correlated with strong correlation (ρ >
%"
%!
), the Vega to the
least volatile asset has the opposite sign as the Vega to the spread
¨ Being long an option on a spread of two strongly correlated assets (usual situation in rates),
usually long the Vega of the most volatile, short Vega of the least volatile
¨ Be careful when the correlation crosses the ratio of volatilities as the buckets will switch sign
34

35. Luc_Faucheux_2020
High Correlation: Caps Vs. Swaption
¨ An average of options is not an option of the average
¨ Another example: ATMF 5x10 cap versus 5y5y European payer swaption
– LIBOR forward rates from 5 years out up to 10 years out are the underlyings for both options
– Cap: A sequence of call options on each individual forward rate
– Payer Swaption: A single call option on the weighted average of the forward rates (the swap rate)
– Correlation between these forward rates impacts the value of the cap versus the swaption
– If the forwards are highly correlated, then when rates change, the 5x10 swap rate will move up or down since all of the
associated forwards tend to move together. Consequently, the caplets on each individual forward rate will be in the money
when the swaption is in the money, and the total payoffs will be similar
Market selloff Market rally
+
-
0
Changes in Forward Rates
Before Option Expires
Cap Payoff
Swaption Payoff
Swap Rate - Case 1
Swap Rate - Case 2
35

36. Luc_Faucheux_2020
Low Correlation: Caps Vs. Swaption
– If the forwards have a low correlation, however, then when rates change, some forwards will go up and
others will go down. As a result, some of the caplets will be in the money, but the swap rate will remain
relatively unchanged so the swaption won’t increase in value. The cap provides a far greater payoff than
the swaption
– Buying a cap and selling the corresponding payer swaption creates a short correlation position
– “An average of options is not an option of the average”
Changes in Forward Rates
Before Option Expires
Cap Payoff
Swaption Payoff
+
-
0
Swap Rate - Case 3
36

37. Luc_Faucheux_2020
Impact of Exotics on Vanilla Markets: The
Gamma Trap
37

38. Luc_Faucheux_2020
Curve Notes: Non-Inversion Notes (fictional dealer)
Achieve high yields (10%) by taking a view that the 2-30s swap curve will not invert
TitleTitleTitle15nc3mo Non-Inversion Note Sample Sales Materials – Non-Inversion Primer
10% Coupon paid each day 30yr CMS >= 2yr CMS
Note Details:
Structure: 15yr nc 3mo
Issuer: Lehman
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 15 years (subject to call)
First Call Date: 3 months
Coupon: 10.00%
** Coupon is floored at 0.00%
** Cpn is paid each day 30YR CMS - 2yr CMS >= 0bps
Frequency/Basis: Quarterly, 30/360, unadjusted
Denominations: TBD
Selling Points:
u The spread between 30yr CMS and 2yr CMS has been positive 99.74% of the
time since June 1992
u The 10% coupon picks 433bps over a new issue 10yr Lehman Corporate Bond
u The coupon needs to accrue 57% of the time to outperform a 10yr Lehman
Corporate Bond
32 38

39. Luc_Faucheux_2020
Leveraged Steepener Notes (fictional dealer)
Leveraged coupon based on the shape of the yield curve
TitleTitleTitle15nc 1Yr Steepener Note Term Sheet
10% Coupon fixed for Year 1,
50*(30YRCMS-10YRCMS) thereafter
(A1/A+/A+)
Note Details:
Structure: 15YR NC 1Yr
Issuer: Single A
Currency: USD
Deal Size: $30mm
Maturity Date: 03/17/22 (subject to call)
First Call Date: 03/17/08, quarterly call
thereafter
Coupon: Year 1: 10.00%
Thereafter: 50* (30YRCMS-10YRCMS)
Coupon set
in advance
Coupon is floored at 0.00%
Frequency/Basis:Quarterly, 30/360, unadjusted
Denominations: 1m/1m
Issue Price: 100.00
35 39

40. Luc_Faucheux_2020
Non Inversion Notes Payoff for investor
¨ Digital Non-Inversion Coupon: 10.00%
Coupon is floored at 0.00%
Coupon is paid each day 30YR CMS - 2yr CMS >= 0bps
¨ Leveraged Steepener Coupon:
Coupon: Year 1: 10.00% Thereafter: 50* (30YRCMS-2YRCMS) set in advance
Coupon is floored at 0.00%
(30-2) CMS
Coupon
0%
10%
50*(30-2) CMS
Coupon
0%
40

41. Luc_Faucheux_2020
Non Inversion Notes Payoff for Exotic desk
¨ Digital Non-Inversion Coupon: 10.00% floored at 0.00%, paid each day 30YR CMS - 2yr CMS >= 0bps
¨ Leveraged Steepener Coupon: 50* (30YRCMS-2YRCMS) floored at 0.00%
(30-2) CMS
Payoff for Exotic dealer
0%
10%
50*(30-2) CMS
Payoff for Exotic dealer
0%
41

42. Luc_Faucheux_2020
Exotic dealer will delta hedge the curve exposure
¨ Digital Non-Inversion Coupon: 10.00% floored at 0.00%, paid each day 30YR CMS - 2yr CMS >= 0bps
¨ Leveraged Steepener Coupon: 50* (30YRCMS-2YRCMS) floored at 0.00%
(30-2) CMS
Payoff for Exotic dealer
0%
10%
50*(30-2) CMS
Payoff for Exotic dealer
0%
42
Coupon paid by dealer
Curve hedge by dealer

43. Luc_Faucheux_2020
Residual exposure from the dealer point of view
¨ Digital Non-Inversion Coupon: LONG DIGITAL FLOOR
¨ Leveraged Steepener Coupon: SHORT LINEAR FLOOR
(30-2) CMS
Payoff for Exotic dealer
0%
10%
50*(30-2) CMS
Payoff for Exotic dealer
0%
43
Coupon paid by dealer
Curve hedge by dealer

44. Luc_Faucheux_2020
Gamma profile
¨ Digital Non-Inversion Coupon: LONG DIGITAL FLOOR
¨ Leveraged Steepener Coupon: SHORT LINEAR FLOOR
(30-2) CMS
Payoff for Exotic dealer
0%
10%
50*(30-2) CMS
Payoff for Exotic dealer
0%
44
Coupon paid by dealer
Curve hedge by dealer

45. Luc_Faucheux_2020
Gamma profile
¨ Digital Non-Inversion Coupon: LONG DIGITAL FLOOR
¨ Leveraged Steepener Coupon: SHORT LINEAR FLOOR
45

46. Luc_Faucheux_2020
Non-Inversion Note Risk
¨ One of the most popular structured notes was before 2008 the non-inversion note
¨ Holder receives an above market coupon, but this only accrues when two points on the swap curve are not inverted
¨ Example: 15yNC3mo 9% 2s10s NIN. Noteholder receives 9% * n/N, where n/N is the fraction of days during the coupon
period on which 10Y CMS – 2Y CMS > 0
¨ On the corresponding swap, the exotics desk is long digital floors on 10Y CMS – 2Y CMS, struck at 0
¨ Dealers actively hedged those by selling linear floors to hedge funds through the “shark fin” structure
¨ Due to the popularity of Non-Inversion Notes and the significant value outstanding, essentially all exotic dealers are long the
same zero-strike digital floors
¨ The Street becomes long Gamma when the curve is slightly upward sloping, but massively short Gamma when the curve
inverts
¨ Noteholders have the opposite Gamma profile, but they normally do not hedge their positions
¨ Consequently, active hedgers are significantly net short Gamma when the curve inverts
¨ Suppose that 2s10s has been positive for some time, but becomes inverted by a few basis points
¨ Exotics desks should be ecstatic, since they no longer have to pay the fixed rate on the swaps for NINs, right?
¨ Investors or notes holder DO NOT dynamically hedge, but the street and the Exotic desks DO dynamically hedge and have to
be under their risk limits
46

47. Luc_Faucheux_2020
A great idea: selling shark find to Hedge Funds
¨ Dealers are long the Digital floor struck at 0% (mostly) because they are paying the
structured coupon X% * n/N, where n/N is the fraction of days during the coupon period on
which 10Y CMS – 2Y CMS > 0 (for example)
¨ Dealers are short the linear floor struck at 0% (mostly) because they are paying the
structured coupon L*(10Y CMS – 2Y CMS), where L is the leverage factor. Because it is
embedded in a note, the coupon cannot become negative (is “floored at 0”), hence the
actual structured coupon is MAX(0, L*(10Y CMS – 2Y CMS))
¨ Dealers want to sell back the Digital floor of payout H and buy back X times the same
amount of linear floor, and then sell back another X times the amount of linear floors struck
at (-H/X) in order to ensure an payout for the hedge fund to be always positive -> the shark
fin
¨ Problem: hedge funds are not stupid, they only did a little and only on the short end of the
market
47

48. Luc_Faucheux_2020
The Gamma Trap
¨ Wrong—Exotics dealers fall into the Gamma trap, which can and has wreaked havoc on their books
– When the curve inverts, exotics desks switch from being long curve Gamma to short curve Gamma
– Dealers have to put on curve flatteners to offset the steepeners they acquire due to Gamma
– With all dealers putting on flatteners at the same time, the market gaps lower since no one is willing to put on a
steepener and get run over
– But, as the curve gets flatter, exotics desks again get put into steepeners because of the short Gamma position, and need
to put on even bigger flatteners
– The curve again gaps flatter, and the cycle repeats. Consequently, the curve goes from being inverted by, say, 5 basis
points to over 50 basis points in a short period of time
– Exacerbating the problem, exotics desks may sell zero-strike linear curve floors against the zero-strike digitals they are
long as a way to monetize the optionality they have bought. This makes dealers even shorter Gamma when the curve
inverts
48

49. Luc_Faucheux_2020
A digital is a limit of a spread of linear options
¨ The digital payoff (top) is the limit of the below payoff when dS -> 0
49
S
Coupon
K
C
S
Coupon
K
C
C
dS

50. Luc_Faucheux_2020
Digital as a limit of vanillas (linear)
¨ Being long a cap of Notional N struck at K and short one of equal notional N struck at (K+dS)
will result of a value for the coupon of dS for the same notional
¨ In order to get a coupon C for a given notional N, the notionals on the linear spread has to
be (N.C/dS)
¨ Let’s call DIGI the value of the digital, and CAP the value of the cap
¨ Both function of strike, underlying, maturity, skew, volatility,….
¨ For a given Notional N and coupon C, the following applies
¨ 𝑁. 𝐶. 𝐷𝑖𝑔𝑖 = lim
&'→)
{
*.,
&'
. 𝐶𝑎𝑝 𝐾 −
*.,
&'
. 𝐶𝑎𝑝(𝐾 + 𝑑𝑆)}
¨ 𝐶𝑎𝑝 𝐾 + 𝑑𝑆 = 𝐶𝑎𝑝 𝐾 + 𝑑𝑆.
#,-.(0)
#0
¨ To the first order, 𝐷𝑖𝑔𝑖(𝐾) = −
#,-.(0)
#0
50

51. Luc_Faucheux_2020
A digital jumps up one order in the greeks
¨ Compared to a linear cap, the digital value is the opposite (-) of the first order derivative of
the linear cap value with respect to the strike K
¨ So the delta of a digital (first order derivative with respect to the underlying) will be equal
and opposite to the second order derivative of the linear with respect to the strike and the
underlier
¨ The Vega of a digital (first order derivative with respect to volatility) will be be equal and
opposite to the second order derivative of the linear with respect to the strike and the
volatility (almost the Vanna, in fact equal to the Vanna in some models, like the normal
Black-Sholes, where the natural variable is (F-K), to contrast with the lognormal Black-Sholes
where the natural variable is Log(F/K))
¨ Digital Vega = Linear Vanna
¨ Digital Delta = Linear Gamma
51

52. Luc_Faucheux_2020
Gamma profile of a linear zero floor
52

53. Luc_Faucheux_2020
Gamma profile of being short a linear zero floor
53

54. Luc_Faucheux_2020
Gamma profile of two linear floors offset to create a Digi
54

55. Luc_Faucheux_2020
Short one linear floor, long another one à long Digi
55

56. Luc_Faucheux_2020
Digi Gamma
56

57. Luc_Faucheux_2020
Dealers are long the digi floor and short the linear floor
¨ Above the strike (positively sloped yield curve), both Gamma offsets each other -> dealers
are flat Gamma on the curve and do not need to actively re-hedge
¨ As the curve starts to flatten, the positive Gamma on the Digital decreases to 0 as the
negative Gamma on the linear floor becomes maximum -> dealers are short Gamma on the
curve, as the curve flattens, dealers get put into a steepener, and start to suffer negative
P&L. In order to reduce their risk, dealers will trade the curve to get into a flattener, pushing
the curve even more into flat to inverted territory
¨ As the curve inverts, the negative Gamma on the linear floor starts to decrease, but the
Gamma on the Digital becomes negative -> dealers become even more negative Gamma on
the curve, and as the curve inverts, dealers get put into massive steepeners creating massive
negative losses, and the only way to reduce risk is to enter into flateners (or receive a
negative rate in forward space, like Morgan Stanley did with Republic of Spain)
¨ This is a perfect example of a ”Gamma trap”, a feedback loop created though dynamic
hedging, that will drive the market. If you are not trading exotics, if you do not know how to
trade exotics, and you do not know the flows, ASK! Dealers are more than happy to talk to
Hedge Funds and tell them about flows, hedging issues and such….
57

58. Luc_Faucheux_2020
The Gamma profile of the dealer books
58
Curve Spread
Pain Scale for exotics dealers
• Grey curve is the Gamma dealers are short from selling linear floors
• Orange curve is the Gamma dealers are long from buying the digi floor
• Red curve is the net of the two : net Gamma position of dealers on the curve

59. Luc_Faucheux_2020
EUR Curve, June 2008 / Strike Concentration
¨ In addition to USD NINs, several EUR NINs have printed. Moreover, most EUR notes were non-callable, whereas the USD
version was typically callable, meaning that the EUR NINs are usually outstanding for much longer
¨ In June 2008, the EUR curve inverted slightly and soon after, provided a textbook case of the Gamma trap: a 30 standard
deviation event, YES I SAID 30 ! Morgan Stanley lost north of 2bn on their exotic books alone and had to restate their
quarterly statement.
¨ Observe also the time of day, when Exotic desks do get a grasp on their risk.
¨ Good luck with your VAR framework protecting you from that…
59

60. Luc_Faucheux_2020
Impact of Callable on the vanilla market
Bermuda skew and an example of rates
sell-off
60

61. Luc_Faucheux_2020
Callable issuance
¨ Most callable issuance tend to have a fixed rate
¨ Investor buys a bond from issuer, pays up the principal, and receives a coupon
¨ Issuer raises funding in that manner, and uses the bond proceeds to finance its business
¨ Issuer will then “swap” the coupon on the bond with a dealer in swap format, with a floating
leg usually representative of the issuer funding spread
¨ When exotic dealer “calls” the swap, the issuer redeem the bond usually at par back to
investor
¨ Investor receives notification of bond redemption, receives principal back and stops
receiving the coupon
61
Exotic Dealer Issuer
Structured Coupon
Floating Rate
+/-
Spread
Investor
Structured Coupon
+
Par at Maturity or when called

62. Luc_Faucheux_2020
Couple of risk factors
¨ From the issuer point of view, one of the risk is if the dealer calls the swap, usually forcing
the issuer to redeem the bond (not always), and having to replace the funding at a
potentially worse level
¨ Dealer will usually call the swap when rates are low (because does not want to keep paying a
fixed rate against floating payments that are now lower than when the deal was initiated)
¨ Could be beneficial for the issuer if rates are lower not because of a major crisis that would
impact its credit, or funding spread, or ability to raise funds
¨ From the investor point of view, when the bond gets called usually at lower rates
environment, the investor now has potentially less opportunities to get a comparable yield
or return with the principal amount he/she just received and needs to maybe reinvest
62

63. Luc_Faucheux_2020
Fixed Callable = Fixed Payer Swap + Bermuda Receiver
¨ In a Fixed Callable swap, the dealer pays a fixed coupon, receives a floating leg and has the
option to “call” the swap, or terminate the transaction
¨ This is equivalent to a Fixed Swap going all the way to maturity, plus a “Bermuda receiver”,
an option to enter into an offsetting receiver swap with same maturity. The start of the
receiver swap is not known in advance
63
Exotic Dealer Issuer
Structured Coupon
Floating Rate
+/-
Spread
Investor
Structured Coupon
+
Par at Maturity or when called

64. Luc_Faucheux_2020
FIXED CALLABLE = FIXED SWAP + BERMUDA RECEIVER
64
Exotic Dealer Issuer
CALLABLE FIXED SWAP
Floating Rate
+/-
Spread
Exotic Dealer Issuer
FIXED SWAP
Exotic Dealer Issuer
BERMUDA RECEIVER
=
+
time

65. Luc_Faucheux_2020
Where do investors get the principal to invest?
¨ Puttable Repo Market, cheap way for investors to raise funds to buy higher yielding assets
like callable issuance. The rate that the investor pays on the principal borrowed is less than
the market rate because the repo originator (bank) has the option to “put” or terminate the
loan
¨ And so the investor sits nicely in between receiving a high coupon on the bond he/she
bought and paying back a lower coupon on the loan he/she entered into in order to buy the
high yielding asset
65
Issuer Investor
Structured Coupon
+
Par at Maturity or when called
Loan
Originator

66. Luc_Faucheux_2020
Where does the loan originator hedges the puttable loan?
¨ Are we starting to see some problem here ? Quite Ourobourian in nature
66
Exotic Dealer Issuer
CALLABLE
Floating Rate
+/-
Spread
Investor
Structured Coupon
+
Par at Maturity or when called
Loan
Originator Exotic Dealer
Floating Rate
+/-
Spread
PUTTABLE

67. Luc_Faucheux_2020
Puttable and Callable, swaps, bonds and repos
67
Exotic Dealer Issuer
CALLABLE
SWAP
Investor
Loan
Originator Exotic Dealer
PUTTABLE
SWAP
CALLABLE
BOND
PUTTABLE
REPO

68. Luc_Faucheux_2020
Another way to look at it
68
Exotic Dealer
Issuer
CALLABLE
SWAP
Investor
Loan
Originator
PUTTABLE
SWAP
CALLABLE
BOND
PUTTABLE
REPO

69. Luc_Faucheux_2020
What an investor to do?
¨ Investor borrows funds at lower than market rate by giving the loan originator the option to
“put” the loan
¨ Investors receives a higher than market rate on the callable bond bought with the loan by
giving the bond issuer the option to “call” the bond.
¨ Rates do not move drastically, the investor benefits from the spread
¨ Rates rally, bond gets called, loan extends, investor gets principal back and might not find an
asset with a return that would still be above the rate that he/she is paying on the loan.
¨ Rates selloff, bond extends, loan gets put, investor now has to refinance himself/herself in a
higher rate environment, and might not find a loan rate lower than the coupon still collected
on the bond
¨ But wait! That is not the whole story. Investors are passive hedgers, exotic dealers are
“dynamic” hedgers, and the callable-puttable structure wreaks havoc to the vanilla and
overall market. A little harder to visualize but bear with me. This is the “double trouble”
¨ Always crucial to figure out who has to do what when the market moves (autocalls in Asia)
69

70. Luc_Faucheux_2020
The impact of the cross delta between funding and rates
¨ The problem of Formosa becomes more complicated when you consider the main risk
factors are:
¨ Rates
¨ Volatility of Rates
¨ Funding curve of the issuer
¨ Volatility of the Funding curve
¨ And the obvious issues with:
¨ Correlation between Rates and Rates volatility (skew)
¨ Correlation between Funding and Rates (cross delta)
¨ Correlation between Funding and Funding volatility (funding skew)
70

71. Luc_Faucheux_2020
71
Bermuda Skew, Rising Rates.
¨ How does it compare with European skew ?
¨ What will happen to a Bermuda book in a sell-off ?
¨ Following the same approach we used to explain the European, we can look at the Vega
profile (how the Vega changes with rates).

72. Luc_Faucheux_2020
72
Bermuda versus European skew.
¨ For the same strike, European payers and receivers have the same skew (put-call parity).
¨ European payers and receivers have the same Vega profile.
¨ Bermuda payers and receivers have different Vega profiles.
¨ Bermuda payers and receivers will have different skew (including on the at-the-money
point).
¨ At-the-money Bermuda will have a non-zero skew adjustment.

73. Luc_Faucheux_2020
The usual pitfall
¨ The common mistake is to say, “oh the 100 basis points high European payer trades in the
market at 1.2% lognormal yield volatility under the at-the-money, so when pricing a 100
basis points high Bermuda I am going to use the same skew adjustment”
¨ The mistake here is not to realize that the skew adjustment on the European is not a ex
nihilo number but comes from the fact that the European has a Vega, Vanna and Volga
profile, and that the market has a different stochastic volatility and correlation between the
rates and the volatility than in the model (which might actually have none of this).
¨ So to get the skew adjustment on the Bermuda, one has to go back to the first principles of
looking at the Vega, Vanna and Volga profile of a Bermuda. Because this profile is VERY
different from a European, it should not be a surprise that the skew adjustment from the
model to the market is different between a European and a Bermuda
¨ In fact, it should come as a shock if it was the same
¨ In particular, an at-the-money Bermuda will exhibit a skew adjustment
73

74. Luc_Faucheux_2020
74
European Vega profile
10NC1 Vega ($/%)
100,000
125,000
150,000
175,000
-100
-80
-60
-40
-20
0
20
40
60
80
100
Rate shifts (basis points)
European Receiver
European Payer

75. Luc_Faucheux_2020
75
Bermuda Profile (equal notional = 100MM)
10NC1 Vega ($/%)
200,000
225,000
250,000
275,000
300,000
325,000
350,000
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
90
100
Rate shifts (basis points)
Bermuda Receiver
Bermuda Payer

76. Luc_Faucheux_2020
76
Bermuda Vega profile (Vega neutral weighting at the money)
(Payer=83MM, Receiver=100MM)
10NC1 Vega ($/%)
200,000
225,000
250,000
275,000
300,000
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
90
100
Rate shifts (basis points)
Bermuda Receiver
Bermuda Payer

77. Luc_Faucheux_2020
77
Hand-waving time for Bermuda Receivers !
¨ When market rallies, we get away from the strike à we lose Vega (-)
¨ we are more likely to exercise, the option is effectively shorter and shorter options have Gamma,
not Vega
SHARP DROP IN VEGA
¨ When rates rise, we get away from the strike à we lose Vega (-)
¨ we are less likely to exercise, the options is effectively longer, and longer options have Vega, not
Gamma
¨ FLAT VEGA PROFILE

78. Luc_Faucheux_2020
78
Hand-waving time for Bermuda payers!
¨ When market rallies, we get away from the strike à we lose Vega (-)
¨ we are less likely to exercise, the option is effectively longer and longer options have Vega, not
Gamma
¨ FLAT VEGA PROFILE
¨ When rates rise, we get away from the strike à we lose Vega (-)
¨ we are more likely to exercise, the options is effectively shorter, and shorter options have Gamma,
not Vega
¨ SHARP DROP IN VEGA

79. Luc_Faucheux_2020
79
Skew around the at-the-money point.
¨ Bermuda Receivers: negative skew premium.
– Rates go up, Vega goes up, Vol goes down à we lose.
– Rates go down, Vega goes down, Vol goes up à we lose.
¨ Bermuda Payers: positive skew premium.
– Rates go up, Vega goes down, Vol goes down à we win.
– Rates go down, Vega goes up, Vol goes up à we win.

80. Luc_Faucheux_2020
80
Bermuda Vega profile
¨ Payers and Receivers Vega profiles “split apart”.
¨ The higher the volatility, the further apart they are.
¨ In a steep yield curve payers will have more Vega than Receivers.
¨ In a steep yield curve, payers will keep more Vega than the receivers when the market rallies
in a parallel way.

81. Luc_Faucheux_2020
81
Bermuda Skew
¨ From a baseline Lognormal model, payers will trade at a skew premium and receivers at a
discount.
¨ Bermuda payers reach maximum Vega for a rate lower than the European forward.
¨ Bermuda receiver reach maximum Vega for a rate higher than the European forward.

82. Luc_Faucheux_2020
82
Market sell-off.
¨ Bermuda Receivers: the option average life increases.
– We get longer Vega.
– We get shorter Gamma.
¨ Bermuda Payers: the option average life decreases.
– We get shorter Vega.
– We get longer Gamma.

83. Luc_Faucheux_2020
83
Impact of a 100bps sell-off on 10NC1Y Bermuda options.
– Receiver: option average life increases from 3.5 to 4.5 years.
– Payer: option average life decreases from 4.5 to 3.5 years.
– Receiver Vega will decrease by 6% only.
– Payer Vega will decrease by 10%.

84. Luc_Faucheux_2020
84
Receivers: Duration and Vega bucketing.
100mm 10NC1 Bermuda Receiver Vega (k$/%)
1 year 2 year 3 year 4 year 5 year 7 year 10 year
1 year - - - - - 19 54 73
18m - - - - - 18 18 36
2 year - - - - - 23 9 32
3 year - - - - 2 27 1 30
4 year - - - - 11 12 - 23
5 year - - 0 9 19 1 - 29
7 year 4 10 15 9 0 - - 38
10 year 14 4 0 - - - - 18
20 year - - - - - - - -
18 14 15 17 32 100 83 279

85. Luc_Faucheux_2020
85
Receivers : impact of a 100bps sell-off
100mm 10NC1 Bermuda Receiver, CHANGE in Vega (k$/%)
1 year 2 year 3 year 4 year 5 year 7 year 10 year
1 year - - - - - (4) (30) (34)
18m - - - - - (7) (7) (14)
2 year - - - - - (2) (1) (3)
3 year - - - - 0 1 0 1
4 year - - - - 2 2 - 5
5 year - - 0 3 4 0 - 7
7 year 2 4 6 3 0 - - 15
10 year 6 2 0 - - - - 8
20 year - - - - - - - -
8 6 6 5 7 (10) (38) (17)

86. Luc_Faucheux_2020
86
Long Bermuda receivers.
¨ Worst case: violent bear steepener with strong skew (strong negative correlation between
rates and yield volatility).
¨ Best case: slow bull flattener with weak skew.

87. Luc_Faucheux_2020
87
Payers: Vega bucketing
100mm 10NC1 Bermuda Payer Vega (k$/%)
1 year 2 year 3 year 4 year 5 year 7 year 10 year
1 year - - - - - (2) 4 2
18m - - - - - 12 12 23
2 year - - - - - 40 16 56
3 year - - - - 4 58 3 65
4 year - - - - 25 27 - 52
5 year - - 0 13 33 3 - 49
7 year 5 13 20 13 0 - - 51
10 year 15 5 0 - - - - 21
20 year - - - - - - - -
20 18 20 26 61 138 34 318

88. Luc_Faucheux_2020
88
Payers: impact of a 100bps sell-off
100mm 10NC1 Bermuda Payer, CHANGE in Vega (k$/%)
1 year 2 year 3 year 4 year 5 year 7 year 10 year
1 year - - - - - 9 5 14
18m - - - - - 10 10 19
2 year - - - - - 4 2 6
3 year - - - - (1) (10) (0) (11)
4 year - - - - (9) (9) - (18)
5 year - - (0) (5) (13) (1) - (19)
7 year (2) (6) (8) (5) (0) - - (21)
10 year (7) (2) (0) - - - - (9)
20 year - - - - - - - -
(9) (8) (8) (10) (23) 2 17 (39)

89. Luc_Faucheux_2020
89
The sell-off double trouble….
¨ Investors:
– Callable Paper extends.
– Structured Repo (putable) gets called away.
– Financing Rate increases.
¨ Hedgers:
– Gamma becomes expensive as dealers get short Gamma.
– Vega sells off as dealers get long Vega.

90. Luc_Faucheux_2020
90
An example of rates selloff in 2004.
1 2 3 4 5 7 10 15 20 30
1 Mon 4.5 7.0 11.4 15.4 18.2 21.2 23.4 24.2 24.2 23.9
3 Mon 6.6 9.2 13.5 17.2 19.8 22.3 24.3 24.9 24.8 24.4
6 Mon 6.7 10.8 15.2 18.7 21.0 23.2 25.0 25.3 25.2 24.7
1 9.7 14.8 18.9 21.9 23.5 25.1 26.4 26.3 26.0 25.5
1.5 15.0 19.5 23.0 24.9 25.9 27.0 27.6 27.2 26.7 26.1
2 20.1 23.8 26.3 27.4 27.9 28.5 28.8 28.0 27.4 26.7
3 27.7 29.7 30.1 30.2 30.1 30.3 29.8 28.7 28.0 27.2
4 31.7 31.4 31.1 30.9 30.9 30.7 29.9 28.8 28.0 27.3
5 31.0 30.8 30.6 30.7 30.7 30.4 29.4 28.4 27.6 27.1
7 30.5 30.7 30.7 30.6 30.3 29.5 28.6 27.7 27.0 26.7
10 30.2 29.5 29.0 28.5 28.1 27.5 27.0 26.2 25.8 25.8
20 24.3 24.1 23.9 23.7 23.6 23.5 23.6 24.1 24.2 23.6
1
M
on6
M
on
1.5
3
5
10
1
4
10
30
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
Option
swap
ATM Swap Rate change 03/07- 03/09
30.0-35.0
25.0-30.0
20.0-25.0
15.0-20.0
10.0-15.0
5.0-10.0
0.0-5.0

91. Luc_Faucheux_2020
91
The normal volatility rising wave.
1 2 3 4 5 7 10 15 20 30
1 Mon 0.78 0.99 1.09 1.15 1.21 1.18 1.15 1.13 1.10 1.12
3 Mon 0.53 0.65 0.70 0.75 0.80 0.78 0.75 0.73 0.71 0.71
6 Mon 0.44 0.48 0.50 0.54 0.58 0.56 0.53 0.51 0.50 0.49
1 0.29 0.31 0.37 0.41 0.42 0.41 0.42 0.38 0.34 0.35
1.5 0.27 0.28 0.32 0.36 0.36 0.35 0.35 0.31 0.29 0.30
2 0.25 0.25 0.28 0.30 0.31 0.28 0.27 0.24 0.24 0.24
3 0.24 0.24 0.26 0.25 0.25 0.23 0.22 0.21 0.22 0.20
4 0.22 0.21 0.22 0.20 0.19 0.19 0.19 0.17 0.19 0.19
5 0.20 0.18 0.17 0.16 0.18 0.17 0.17 0.17 0.15 0.17
7 0.18 0.17 0.16 0.15 0.17 0.16 0.16 0.16 0.14 0.16
10 0.18 0.18 0.18 0.17 0.16 0.15 0.14 0.14 0.12 0.15
20 0.07 0.07 0.06 0.06 0.06 0.06 0.05 0.05 0.05 0.06
1
M
on6
M
on
1.5
3
5
10
1
4
10
30
0.00
0.20
0.40
0.60
0.80
1.00
1.20
1.40
Option
Swap
BPs Volatility Changes change 03/07 - 03/09
1.20-1.40
1.00-1.20
0.80-1.00
0.60-0.80
0.40-0.60
0.20-0.40
0.00-0.20

92. Luc_Faucheux_2020
92
The Lognormal volatility twist.
1 2 3 4 5 7 10 15 20 30
1 Mon 3.12 3.52 3.52 3.42 3.40 3.11 2.84 2.68 2.59 2.61
3 Mon 1.84 2.02 1.92 1.86 1.86 1.66 1.48 1.40 1.36 1.37
6 Mon 1.38 1.28 1.11 1.05 1.03 0.89 0.75 0.72 0.70 0.70
1 0.60 0.41 0.43 0.45 0.38 0.32 0.35 0.30 0.25 0.31
1.5 0.23 0.08 0.09 0.16 0.13 0.06 0.09 0.08 0.09 0.14
2 -0.05 -0.18 -0.19 -0.14 -0.09 -0.16 -0.15 -0.12 -0.06 0.00
3 -0.38 -0.42 -0.34 -0.34 -0.34 -0.33 -0.30 -0.19 -0.11 -0.10
4 -0.55 -0.53 -0.47 -0.47 -0.47 -0.43 -0.34 -0.27 -0.18 -0.14
5 -0.52 -0.54 -0.55 -0.54 -0.47 -0.44 -0.35 -0.24 -0.25 -0.16
7 -0.46 -0.46 -0.47 -0.46 -0.35 -0.35 -0.29 -0.20 -0.21 -0.14
10 -0.29 -0.24 -0.22 -0.22 -0.23 -0.21 -0.22 -0.15 -0.17 -0.09
20 -0.32 -0.31 -0.32 -0.29 -0.29 -0.29 -0.28 -0.25 -0.24 -0.21
1Mon
6Mon
1.5
3
5
10
1
4
10
30
-0.75
0.00
0.75
1.50
2.25
3.00
3.75
4.50
Option
Swap
Yield Volatility Changes change 03/07 - 03/09
3.75-4.50
3.00-3.75
2.25-3.00
1.50-2.25
0.75-1.50
0.00-0.75
-0.75-0.00

93. Luc_Faucheux_2020
93
A sharp correction against a bigger picture?
5y5y Normal Vol vs. ATM Forward Rate
4.00
4.50
5.00
5.50
6.00
6.50
7.00
7.50
8.00
8.50
9.00
4.00 4.50 5.00 5.50 6.00 6.50 7.00 7.50 8.00 8.50
ATM Forward Rate
BasisPointVol

94. Luc_Faucheux_2020
9
4
Lognormal volatility / forward rates correlation.
5y5y Yield Vol vs. ATM Forward Rate
4.00
9.00
14.00
19.00
24.00
29.00
4.00 4.50 5.00 5.50 6.00 6.50 7.00 7.50 8.00 8.50
ATM Forward Rate
YieldVol

95. Luc_Faucheux_2020
95
5y5y correlation.
¨ Historically Lognormal volatility decreases 3% for every 100bps rise in rates.
¨ Over that week selloff, Lognormal volatility only decreased by 0.5% for a 30bps rise in rates.
¨ Increased market expectation of volatility in the belly of the curve.

96. Luc_Faucheux_2020
96
The wheel of fortune.
5y5y Normal Vol vs. ATM Forward Rate
4.00
4.50
5.00
5.50
6.00
6.50
7.00
7.50
8.00
8.50
9.00
4.00 4.50 5.00 5.50 6.00 6.50 7.00 7.50 8.00 8.50
ATM Forward Rate
BasisPointVol
1998
2000
2003
2004
2002 2001
1999

97. Luc_Faucheux_2020
97
The wheel of fortune?
¨ “Inconsistency is my very essence” says the wheel. “Raise yourself up on my spokes if you
wish, but do not complain when you are plunged back down”.
Tony Wilson.(*)
¨ (*) maybe also Boethius, am not sure, would have to get back to you on that one.

98. Luc_Faucheux_2020
98
Summary.
¨ Bermuda payers and receivers have asymmetrical Vega profiles, hence different skew
adjustments for the same strike.
¨ Best hedge against being long Bermuda receivers in a market selloff is being long Bermuda
payers. BUY 10NP2Y.
¨ This might seems counterintuitive, as the best hedge against being long an option is buying
another option
¨ Second best hedge is to be short caps and long short-dated high strike payers.

99. Luc_Faucheux_2020
Appendix: Sample Marketing Materials
(so that we do not make any people jealous, we intentionally picked a
fictitious dealer)
99

100. Luc_Faucheux_2020
Front-End Floaters: Constant Maturity Treasury
A substantial amount of CMT has printed in the market due to views on the front-end
TitleTitleTitle1yr CMT Floating Rate Note Sample Sales Materials – The CMT Primer
Coupon pays the 1yr CMT rate
Note Details:
Structure: 1yr Fixed Maturity (not callable)
Issuer: FHLB
Deal Size: 450mm
CUSIP: 3133XK4U6
Maturity: 1 year
Coupon: 1Yr CMT + 30 bps (per Fed Page H15)
Frequency: Monthly pay / reset, 30/360, unadjusted
Denomination: $1,000
Selling Points:
¨ Occasional upfront Pickup to libor floaters and agency bullets
¨ CMT is an index easily viewable on Bloomberg (H15T1Y <Index> HP)
¨ 1yr CMT approximates the current 1yr U.S. Treasury rate
¨ Unique cash offering that fades recent market Fed expectations
¨ Monthly coupon resets
100

101. Luc_Faucheux_2020
Front-End Floaters: Best of CMT Note
Do you think the curve will steepen or flatten? Get paid the peak of the UST curve …
TitleTitleTitle2yr ‘Best of CMT’ Note Sample Sales Materials – ‘Best of CMT’ Termsheet
Coupon pays the highest of 2yr CMT, 10yr CMT or 30yr CMT
Note Details:
Structure: 2yr Fixed Maturity (not callable)
Issuer: Lehman
Deal Size: TBD
Maturity: 2 years
Indexes: 2yr CMT, 10yr CMT and 30yr CMT
Coupon: The greatest of the three indexes noted above
** Coupon is floored at 1.00%
Frequency/Basis: Quarterly pay / reset, 30/360
Denomination: $1,000
Selling Points:
u Structure is totally customizable to an investor's preferences
u Instead of taking a view on where a particular point in the curve is,
ensure that you receive the highest point among the indexes selected
u CMT is a liquid index published on Fed page H15 (available via Reuters,
Bloomberg, and other data sources)
u Coupons reset quarterly)
u Returns are 100% principle-protected and floored at 1%
27 101

102. Luc_Faucheux_2020
Front-End Floaters: CMS Floater
Do you think the market will re-price Fed expectations?
TitleTitleTitle2yr CMS Floating Rate Note Sample Sales Materials – CMS Floater Termsheet
Coupon pays the 2yr CMS rate
Note Details:
Structure: 2yr Fixed Maturity (not callable)
Issuer: Lehman
Deal Size: TBD
CUSIP: TBD
Maturity: 2 years
Coupon: 2Yr CMS (Constant Maturity Swap Rate)
Frequency/Basis: Monthly pay / reset, 30/360, unadjusted
Denomination: $1,000
Selling Points:
¨ Monthly coupons resets
¨ CMS is a rate easily viewable on Bloomberg (USSWAP2 <Index> HP)
¨ Front end curve steepening play
¨ Note outperforms if 2Yr CMS is greater than 1mo Libor
28 102

103. Luc_Faucheux_2020
Callable Capped Floater
Achieve enhanced yield with a floating rate by selling a cap and a call option
TitleTitleTitle10nc6mo Callable Capped Floater Sample CCF Termsheet
3mL + 72bps, 6.50% Cap
Note Details:
Structure: 10yr nc 6mo
Issuer: FHLB (AAA/Aaa)
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 10 years (subject to call)
First Call Date: 6 months
Coupon: 3m LIBOR + 0.72%
Cap: 6.50%
Frequency/Basis: Quarterly, 30/360, unadjusted
Denominations: $1,000
Selling Points:
u Forward 3m LIBOR plus 72bps is still 38bps below cap
u Picks 40bps to comparable maturity bullets
29 103

104. Luc_Faucheux_2020
Range Notes
Achieve enhanced yield by taking a view that short-term rates will be range bound
TitleTitleTitle15nc3mo Range Note Sample Sales Materials – Range Note Primer
8% Coupon paid each day 6m LIBOR is between 0 and 7%
Note Details:
Structure: 15yr nc 3mo
Issuer: AAA
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 15 years (subject to call)
First Call Date: 3 months
Coupon: 8.00%
** Coupon is floored at 0.00%
** Cpn is paid each day 6m LIBOR is between 0 and 7%
Frequency/Basis: Quarterly, 30/360, unadjusted
Denominations: $1,000
Selling Points:
u In the past 15yrs, 6mo LIBOR has been within the range (less than or equal to
7.00%) 99.7% of the time
u Current 6mo LIBOR forward curve projects a maximum value of 5.47%
(153bps of cushion vs. the range top) over the life of the trade, implying that
the note will always be within range and the maximum coupon will be paid, if
not called
30 104

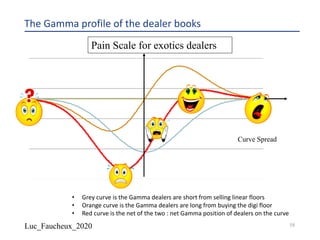
105. Luc_Faucheux_2020
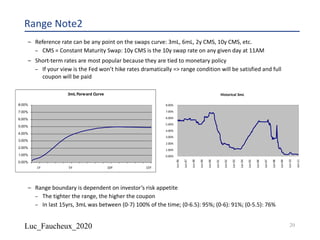
Lehman Brothers 1yr “Wedding Cake” Range Note
Single coupon at maturity if 6-month USD Libor remains within 1 of 3 ranges
“Wedding Cake” Structured Note Format
u If the First Barrier Range condition is met: [10.00%];
u Else if the First Barrier Range condition is NOT met but the Second
Barrier range is met: [8.00%];
u Else if NEITHER the First and Second Barrier Range conditions are
met but the Third Barrier range is met: [6.00%];
u Else if NONE of the Barrier Range conditions are met: 0.00%.
Lower Barrier Upper BarrierContingent
Coupon
[10.00%]
[8.00%]
[6.00%]
5.25%
5.125
%
5.00%
5.50%
5.625
%
5.75%
100%
Principal
Protection
Lehman Brothers’ U.S. Economic Outlook At A Glance
u Lehman Brothers US Economics team predicts a Fed on hold in 2007
u If this is realized, 6-month Libor should stay fairly level in 2007 as 6-
month Libor and Fed Funds are highly correlated (hist. r^2 = .972)
u Today’s Libor setting is 5.394%
31 105

106. Luc_Faucheux_2020
Curve Notes: Non-Inversion Notes
Achieve high yields (10%) by taking a view that the 2-30s swap curve will not invert
TitleTitleTitle15nc3mo Non-Inversion Note Sample Sales Materials – Non-Inversion Primer
10% Coupon paid each day 30yr CMS >= 2yr CMS
Note Details:
Structure: 15yr nc 3mo
Issuer: Lehman
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 15 years (subject to call)
First Call Date: 3 months
Coupon: 10.00%
** Coupon is floored at 0.00%
** Cpn is paid each day 30YR CMS - 2yr CMS >= 0bps
Frequency/Basis: Quarterly, 30/360, unadjusted
Denominations: TBD
Selling Points:
u The spread between 30yr CMS and 2yr CMS has been positive 99.74% of the
time since June 1992
u The 10% coupon picks 433bps over a new issue 10yr Lehman Corporate Bond
u The coupon needs to accrue 57% of the time to outperform a 10yr Lehman
Corporate Bond
32 106

107. Luc_Faucheux_2020
Dual Barrier Range Accrual
Achieve enhanced yield by taking view on short-term rate levels and curve shape
TitleTitleTitle15nc3mo Dual Barrier Range Note Sample Dual Barrier Termsheet
10% Coupon paid subject to two conditions
Note Details:
Structure: 15yr nc 3mo
Issuer: AA
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 15 years
First Call Date: 3 months
Coupon: 10.00%
** Coupon is floored at 0.00%
** Coupon paid each day 6m LIBOR is between 0 and
7% AND 30yr CMS – 2yr CMS >= 0
Frequency/Basis: Quarterly, 30/360, unadjusted
Denominations: $1,000
Selling Points:
u In the past 15yrs, 6mo LIBOR has been within the range (less than or equal to
7.00%) 99.7% of the time
u The spread between 30yr CMS and 2yr CMS has been positive 99.74% of the
time since June 1992
u The 10% coupon picks 430bps over a new issue 10yr Lehman Corporate Bond
33 107

108. Luc_Faucheux_2020
Curve Notes: Collared Steepness Note
Floored Steepness Note: A low-risk steepening view
TitleTitleTitle10nc1yr Collared Steepness Note Sample Sales Materials – Steepness Primer
Coupon Pays 8.00% for the 1st year; 10 times the 2s-10s Swap Curve thereafter
Note Details:
Structure: 10yr nc 1yr
Issuer: Lehman Brothers
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 10 years (subject to call)
First Call Date: 1 year, quarterly call thereafter
Coupon: Year 1: 8.00%
Years 2-10: 10 * (10yr CMS Rate - 2yr CMS
Rate)
** Coupon is floored at 4.00%
** Coupon is capped at 11.00%
Frequency/Basis: Quarterly, Act/Act, unadjusted
Denominations: TBD
Selling Points:
u Yield to Worst = 4.5485% (i.e. a low risk steepening view)
u Front fixed coupon of 8.00% picks 173bps over a comparable Agency new
issue 10nc1yr fixed rate bond
u The historical steepness of the 2s-10s Swap Curve on average for the past
15yrs is 122.2bps (implying a coupon of 11.00% if not called)
u The 2s-10s Swap curve would have to steepen only 48bps (.57 of one
historical standard deviation) in order to outperform a Lehman Brothers
10nc1yr Fixed Rate Callable (6.27%).
34 108

109. Luc_Faucheux_2020
Leveraged Steepener Notes
Leveraged coupon based on the shape of the yield curve
TitleTitleTitle15nc 1Yr Steepener Note Term Sheet
10% Coupon fixed for Year 1,
50*(30YRCMS-10YRCMS) thereafter
(A1/A+/A+)
Note Details:
Structure: 15YR NC 1Yr
Issuer: Single A
Currency: USD
Deal Size: $30mm
Maturity Date: 03/17/22 (subject to call)
First Call Date: 03/17/08, quarterly call
thereafter
Coupon: Year 1: 10.00%
Thereafter: 50* (30YRCMS-10YRCMS)
Coupon set
in advance
Coupon is floored at 0.00%
Frequency/Basis:Quarterly, 30/360, unadjusted
Denominations: 1m/1m
Issue Price: 100.00
35 109

110. Luc_Faucheux_2020
LIFT Notes (Laddered Inverse Floaters) / Snowball
Achieve enhanced yield while expressing bullish rate view
TitleTitleTitle5nc3mo Lift Note Sample Lift Note Termsheet
Snowball Coupon Structure
Note Details:
Structure: 5yr nc 3mo
Issuer: Lehman Brothers
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 5 years (subject to call)
First Call Date: 3 months
Coupon: Yr 1: 8.50% fixed
Yr 2: previous coupon + 5.0% - 6m LIBOR (in arrears)
Yr 3: previous coupon + 6.0% - 6m LIBOR (in arrears)
Yr 4: previous coupon + 7.0% - 6m LIBOR (in arrears)
Yr 5: previous coupon + 8.0% - 6m LIBOR (in arrears)
Frequency/Basis: Quarterly, 30/360, unadjusted
Denominations: $1,000
Selling Points:
u Above market year 1 coupon
u Potential yield pick-up over bullets or vanilla callables
u Coupons “snowball” if bullish rate view realized
u Note can be customized to multiple rate views/ bearish alternatives available
upon request
36 110

111. Luc_Faucheux_2020
TARN (Target Redemption Notes)
Achieve enhanced yield by taking view that rates will be lower than implied forwards
TitleTitleTitle10 Year TARN Sample TARN Termsheet
Note Details:
Structure: 10 Year Bullet
Issuer: Lehman Brothers
Currency: USD
Deal Size: TBD
CUSIP: TBD
Maturity Date: 10 years
First Call Date: non callable
Coupon: Year 1: 10%
Years 2-10: 12% - (2*USD Libor in arrears)
**subject to automatic early redemption/Lifetime cap
Frequency/Basis: Quarterly, 30/360, unadjusted
Lifetime Cap: 12.0% of Principal Amount
The Lifetime Cap sets a maximum of the aggregate amount
of coupon that will be paid over the life of the Notes. If on any
Coupon Payment Date the Lifetime Cap is reached, the
Notes shall be redeemed at par on such Coupon Payment Date.
Denominations: $1,000
Selling Points:
u Relatively shorter duration compared to 10yrNC18mo Range Note
37 111

112. Luc_Faucheux_2020
Curve Notes: Auto-Callables
Contingent Coupon of 9% is paid if the 2s-10s Swap Curve exceeds 50bps within 3yrs
TitleTitleTitle3yr Auto-Callable Sample Coupon Payment Schedule
15yr History of the 2s-10s Swap Curve 15yr History of the 2s-10s Swap Curve
Issuer Single A Issuer
Final Maturity: 3yrs (subject to termination event)
Coupon: If 10yrCMS - 2yrCMS exceeds .50% on
any observation date, coupon pays
9.00% per annum (and note is
terminated)
Returns are floored at zero
Observation Freq: Semi-annual
10YR CMS is the 10Yr USD Swap ref published on Reuters
Screen ISDAFIX1 Page and 2YR CMS is the 2Yr USD Swap ref
published on Reuters Screen ISDAFIX1 Page in each case ,
determined 2 NY and London Business Days prior to each reset
date.
Sample
Coupon
Dates
If 10yr CMS
minus 2yr
CMS >=
.50%
If 10yr CMS
minus 2yr
CMS < .50%
Settlement 7/26/2006
1/26/2007 104.50 -
7/26/2007 109.00 -
1/26/2008 113.50 -
7/26/2008 118.00 -
1/26/2009 122.50 -
Final Maturity 7/26/2009 127.00 100.00
(per $100)
Redemption Amount
-50.00
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
Jun-91 Mar-94 Dec-96 Sep-99 May-02 Feb-05
10s-2s in bps
10s - 2s Swap Curve 0bp Threshold
Ø The current spread between 2yr and 10yr Swap Rates is 9.8bps. The
standard deviation of this relationship is approximately 80bps, thus
the curve would need to steepen .5 of one standard deviation (before
the contractual maturity) in order for the notes to redeem with a 9%
annualized return.
Ø Maintaining the current level, however, implies a 0% coupon and a
return of principal in 3yrs (100% Principal Protection).
38 112

113. Luc_Faucheux_2020
Inflation Bonds: CPI Floaters
The most transparent way to buy Inflation protection ...
TitleTitleTitleCPI Floating Rate Note Sample Sales Materials – CPI Primer
Coupon pays 2.30% plus the year over year change in CPURNSA
SLM Corp (A/A2/A+)
Note Details:
Structure: 7yr Fixed Maturity (not callable)
Issuer: Lehman Brothers, Inc.
Currency: USD
Deal Size: $135mm
CUSIP: 78442FBH0
Maturity Date: 11/01/13
Coupon: 2.30% + YOY Change in CPI (CPURNSA)
Frequency/Basis: Monthly, Act/Act, unadjusted
Denominations: 10m/1m
Selling Points:
u The YOY change has never been negative in recorded history
u 230bps is one of the highest spreads over the YOY change in headline CPI we
have in inventory
u The Price-adjusted baseline pick to similar maturity TIPS is 40bps
u Based on current CPURNSA readings, the following coupons are set:
April 1 = 5.72%
May 1 = 6.29%
June 1 = 5.89%
u Achieve a monthly nominal coupon based on changes in inflation without
notional fluctuations
39 113