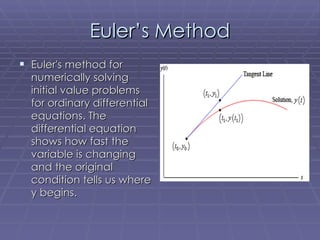
Leonhard Euler was an 18th century Swiss mathematician known as "the Cyclops" due to his lazy right eye. He had exceptional mental calculation skills and memory. Some of Euler's most important contributions to mathematics include Euler's identity, which utilizes five fundamental constants; Euler's polyhedral formula relating the numbers of faces, edges and vertices of polyhedra; and Euler's method for solving differential equations. Euler also studied the nine-point circle construction of triangles.

1. Leonhard Euler Mathematician/Physicist By: Xuxa Baptiste

2. Determination of the Cyclops Swiss mathematician Leonhard Euler was one the greatest mathematicians of the 18 th century. His lazy right eye led many to call him “the Cyclops.” He had exceptional mental calculation skills and a capacious photographic memory. Leonhard could recite Virgil’s Aeneid word for word without stopping.

3. Euler’s Identity Considered by many to be one of the most remarkable expressions ever, Euler’s identity utilizes 5 of the most fundamental constants. e - Euler’s number and the base of natural logarithms i – imaginary number that is the square root of negative 1 Pi -ratio of the circumference of a circle to its diameter 0 and 1 can act as both constants or standard integers.

4. Euler’s Polyhedral Formula The Euler's Theorem, also known as the Euler's formula, deals with the relative number of faces, edges and vertices that a polyhedron (or polygon) may have. A polyhedron is a geometric solid with straight edges and flat faces. The number of vertices minus the number of edges, plus the number of faces is equal to two.

5. Euler’s Method Euler's method for numerically solving initial value problems for ordinary differential equations. The differential equation shows how fast the variable is changing and the original condition tells us where y begins.

6. Nine Point Circle The nine point circle is a circle that can be constructed out of any triangle. The name comes from the 9 significant points identified by the triangle. They are the 3 midpoints of every side of the triangle, 3 altitudes, and the 3 midpoints of the line segment form the vertex to the orthocenter.

7. Euler’s Number e is one of the most unique and important numbers in mathematics. It is a real and irrational number so that the slope of the tangent line of the exponential function at the point x=0 is exactly 1. 2.718055556

8. The Cyclops Approves This Presentation

9. Works Cited Page &quot;Differential Equations -- Euler's method in Pictures.&quot; Math Page . Web. 23 Nov. 2009. <http://www.math.montana.edu/frankw/ccp/calculus/des/euler-pictures/learn.htm>. &quot;E - Euler's number.&quot; Math is Fun - Maths Resources . Web. 23 Nov. 2009. <http://www.mathsisfun.com/numbers/e-eulers-number.html>. &quot;Euler's Mathematical Contributions: The Work of One of the Greatest Minds in Mathematical History | Suite101.com.&quot; Math/Chaos Theory | Suite101.com . Web. 22 Nov. 2009. <http://mathchaostheory.suite101.com/article.cfm/eulers_mathematical_contributions>. &quot;Euler's polyhedron formula.&quot; Plus Magazine . Web. 23 Nov. 2009. <http://plus.maths.org/issue43/features/kirk/index.html>. &quot;Formulating Euler's Identity: An Exploration of One of History's Greatest Equations | Suite101.com.&quot; Math/Chaos Theory | Suite101.com . Web. 22 Nov. 2009. <http://mathchaostheory.suite101.com/article.cfm/formulating_eulers_identity>. &quot;Nine-point circle - Teaching Resource - Metallurgy and Materials Science & Engineering.&quot; Teaching Resource - Materials Science and Engineering . Web. 23 Nov. 2009. <http://viet4777.vatlieu.us/ultilities.html?view=mediawiki&article=Nine-point_circle>.