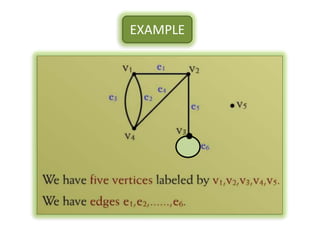
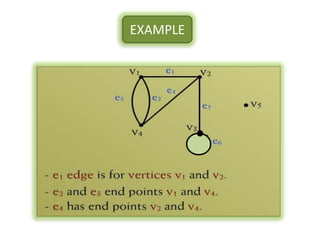
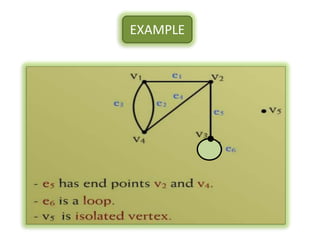
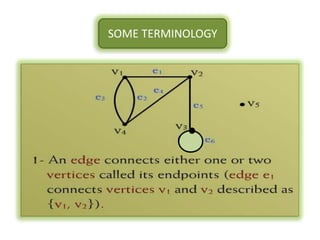
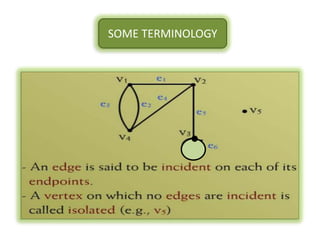
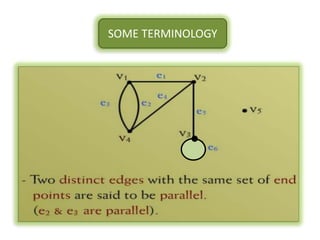
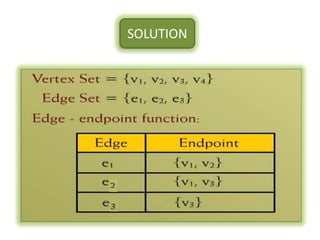
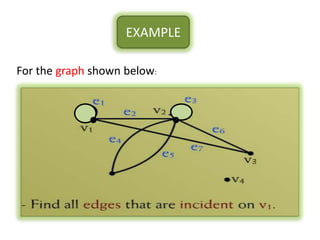
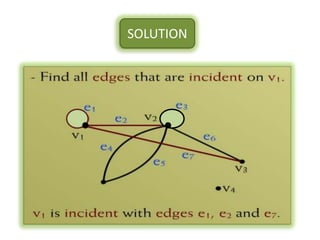
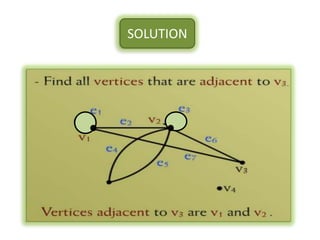
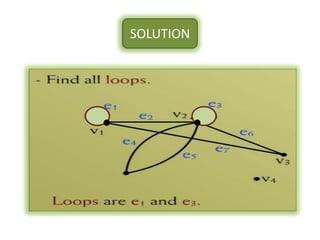
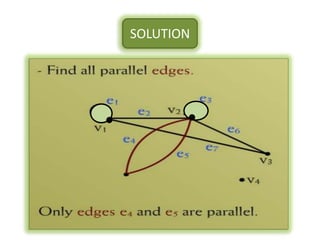
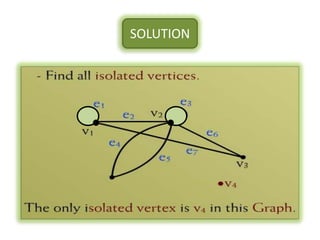
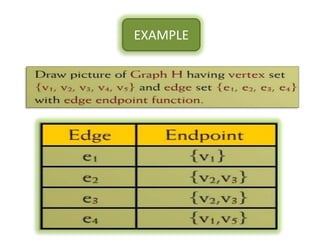
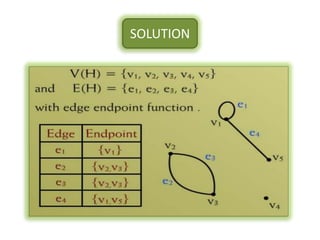
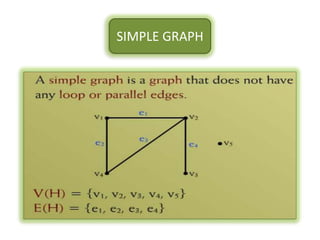
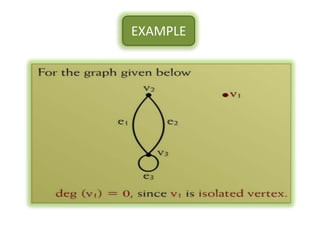
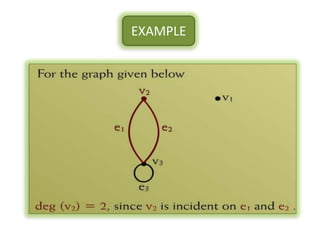
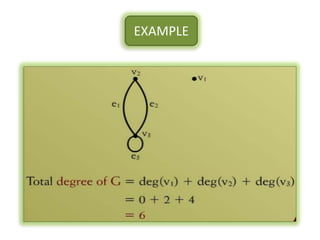
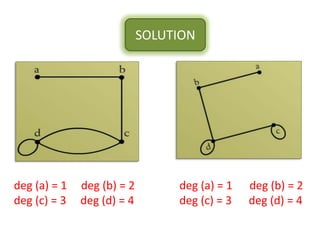
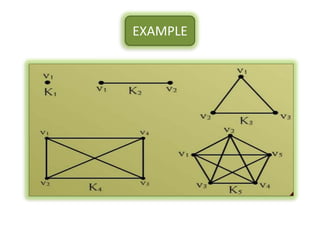
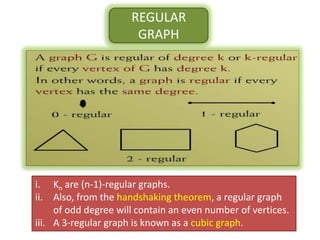
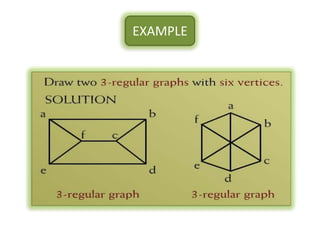
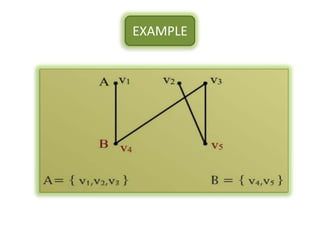
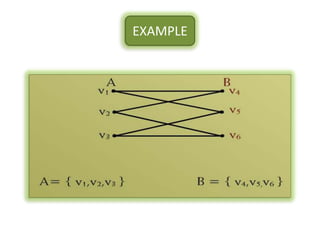
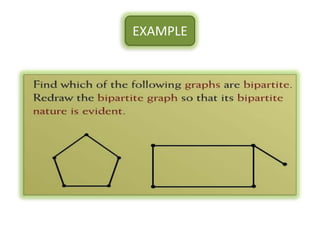
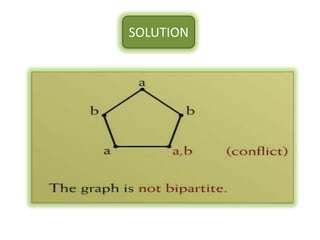
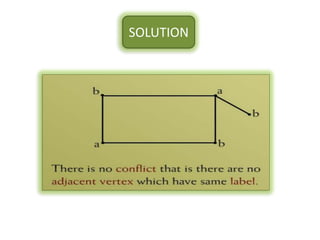
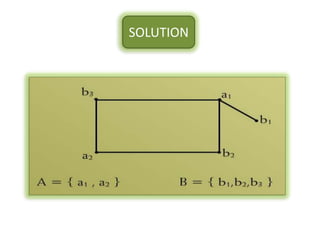
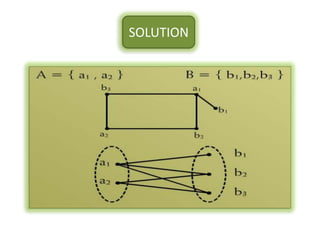
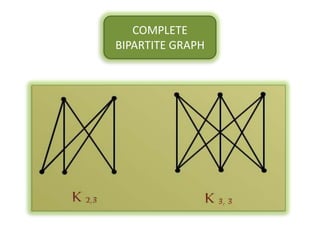
The document is a lecture on discrete structures focusing on graph theory, outlining definitions and terminology such as vertices and edges. It discusses concepts including the degree of a vertex, the handshaking theorem, and provides examples and exercises related to simple, complete, and bipartite graphs. Additionally, it highlights properties of regular graphs and cubic graphs.

1. Discrete Structures
Lecture # 12
Dr. Muhammad Ahmad
Department of Computer Science
FAST -- National University of Computer and
Emerging Sciences. CFD Campus
Material Partially Collected by Prof. Dr. A.M. Khan, Slides Prepared by Dr. M. Ahmad

2. GRAPH
A graph is a non-empty set of points called vertices
and a set of line segments joining pairs of vertices
called edges.

3. GRAPH
Formally, a graph G consists of two finite sets:
(1) A set V=V(G) of vertices (or points or nodes)
(2) A set E=E(G) of edges.
Where each edge corresponds to a pair of vertices.

4. EXAMPLE

5. EXAMPLE

6. EXAMPLE

7. SOME TERMINOLOGY

8. SOME TERMINOLOGY

9. SOME TERMINOLOGY

10. SOME TERMINOLOGY

11. EXAMPLE
Define the following graph formally by specifying its
vertex set, its edge set, and a table giving the edge
endpoint function.

12. SOLUTION

13. EXAMPLE
For the graph shown below:

14. EXAMPLE

15. SOLUTION

16. SOLUTION

17. SOLUTION

18. SOLUTION

19. SOLUTION

20. EXAMPLE

21. SOLUTION

22. SIMPLE GRAPH

23. DEGREE OF A
VERTEX
Let G be a graph and “v” a vertex of G. The degree
of “v”, denoted deg(v), equal the number of edges
that are incident on “v”, with an edge that is a loop
counted twice.
The total degree of G is the sum of the degrees of
all the vertices of G.

24. EXAMPLE

25. EXAMPLE

26. EXAMPLE

27. EXAMPLE

28. HANDSHAKING
THEOREM

29. EXAMPLE

30. SOLUTION

31. SOLUTION

32. SOLUTION
deg (a) = 1 deg (b) = 2
deg (c) = 3 deg (d) = 4
deg (a) = 1 deg (b) = 2
deg (c) = 3 deg (d) = 4

33. EXAMPLE

34. EXERCISE
In a group of 15 people, is it possible for each
person to have exactly 3 friends ?

35. EXERCISE
In a group of 15 people, is it possible for each
person to have exactly 3 friends ?
Answer: No because of handshaking theorem.

36. COMPLETE
GRAPH

37. EXAMPLE

38. EXERCISE
i. Degree of each vertex is n-1
ii. deg(Kn) = n(n-1) =2m
iii.No. of edges = m = n(n-1)/2

39. REGULAR
GRAPH
i. Kn are (n-1)-regular graphs.
ii. Also, from the handshaking theorem, a regular graph
of odd degree will contain an even number of vertices.
iii. A 3-regular graph is known as a cubic graph.

40. EXAMPLE

41. BIPARTITE
GRAPH

42. EXAMPLE

43. EXAMPLE

44. DETERMINING
BIPARTITE GRAPH

45. DETERMINING
BIPARTITE GRAPH

46. EXAMPLE

47. SOLUTION

48. SOLUTION

49. SOLUTION

50. SOLUTION

51. COMPLETE
BIPARTITE GRAPH
No. of edges in Km,n is given by mn.

52. COMPLETE
BIPARTITE GRAPH