Downloaded 21 times
Uploaded byFaisal Mehmood
Lecture 04
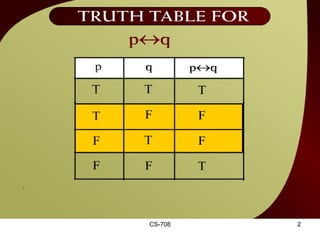
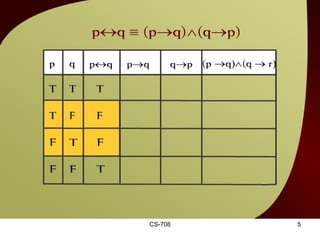
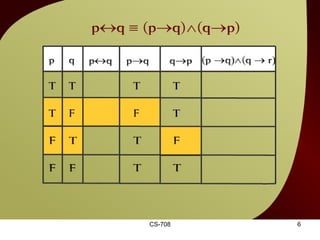
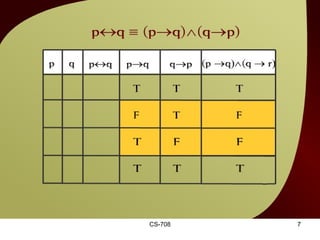
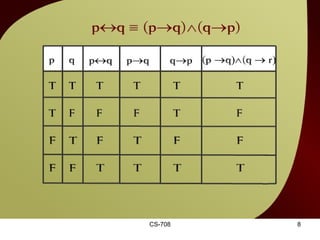
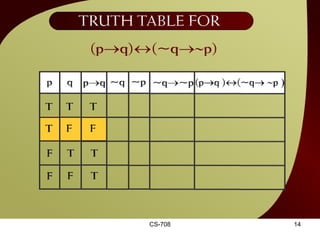
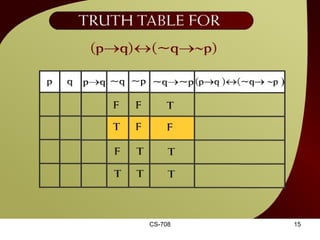
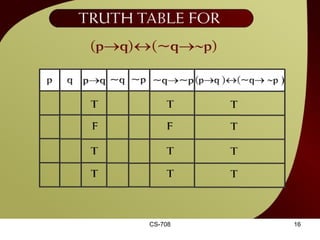
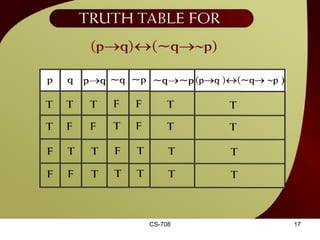
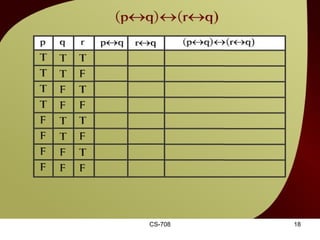
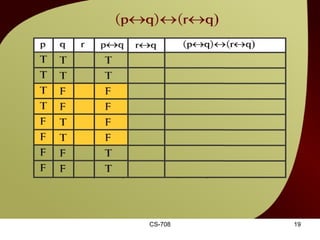
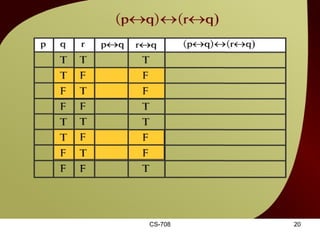
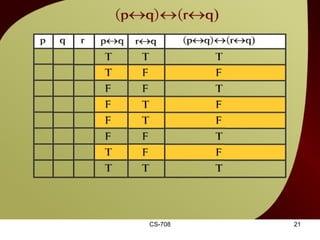
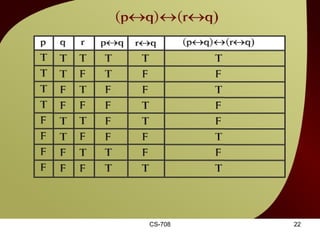
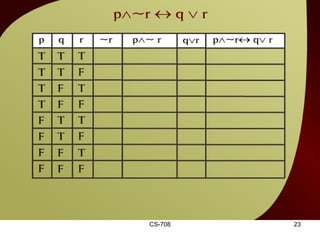
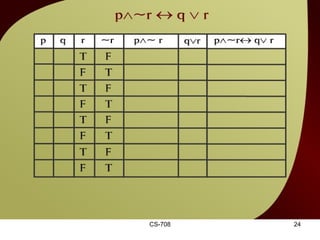
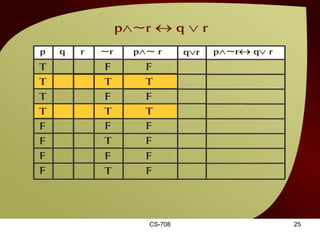
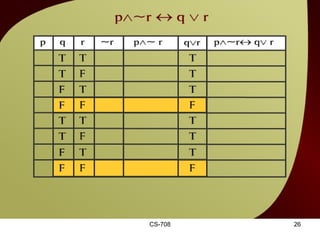
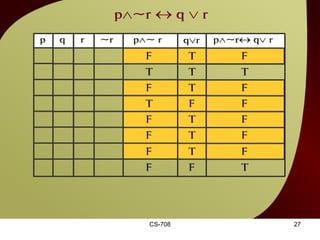
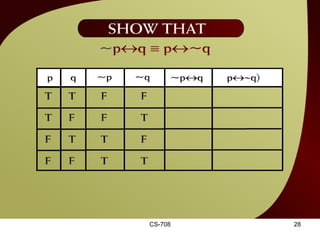
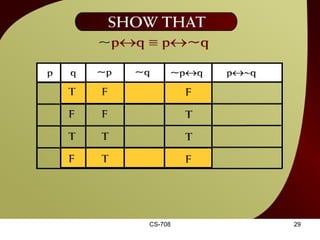
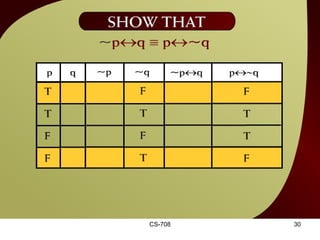
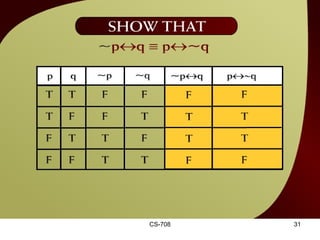
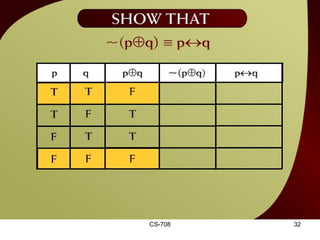
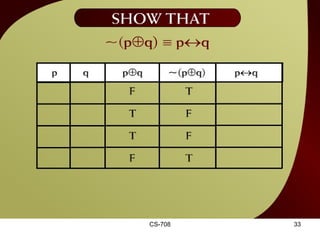
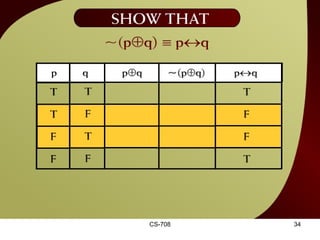
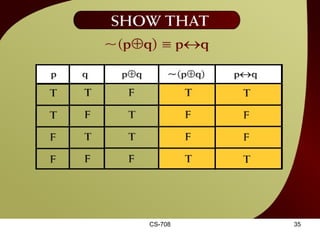
The document contains sections from a course on logic and logical operators like biconditional, disjunction, conjunction and negation. It includes truth tables to define logical expressions, examples of applying logical operators, and exercises to practice logical equivalence and applications of logical laws.
More Related Content
Lecture 04
- 1.
- 2. CS-708 Truth Tablefor p <--> - 3
- 3.
- 4.
- 5. CS-708 p q = (p q) (q p) – 5a v
- 6. CS-708 p q = (p q) (q p) – 5b v
- 7. CS-708 – 5c p q = (p q) (q p) – 5c v
- 8. CS-708 v p q = (p q) (q p) – 5
- 9.
- 10.
- 11.
- 12.
- 13.
- 14. CS-708 Truth tablefor (p q) (~q ~p) – 7a
- 15. CS-708 Truth tablefor (p q) (~q ~p) – 7b
- 16. CS-708 Truth tablefor (p q) (~q ~p) – 7c
- 17. CS-708 Truth tablefor (p q) (~q ~p) – 7
- 18. CS-708 (p q) (r q) – 8
- 19. CS-708 (p q) (r q) – 8b
- 20. CS-708 (p q) (r q) – 8c
- 21. CS-708 (p q) (r q) – 8d
- 22. CS-708 (p q) (r q) – 8
- 23. CS-708 p ~ r q v r – 10 v
- 24. CS-708 p ~ r q v r – 10b v
- 25. CS-708 p ~ r q v r – 10c v
- 26. CS-708 p ~ r q v r – 10d v
- 27. CS-708 p ~ r q v r – 10e v
- 28. CS-708 Show that~p q ≡ p ~q – 11a
- 29. CS-708 Show that~p q ≡ p ~q – 11b
- 30. CS-708 Show that~p q ≡ p ~q – 11
- 31. CS-708 Show that~p q ≡ p ~q – 11c
- 32. CS-708 Show that~(p + q) ≡ p q – 12b
- 33. CS-708 Show That- 1(4 - 2c)
- 34. CS-708 Show that~(p + q) ≡ p q – 12d
- 35. CS-708 Show that~(p + q) ≡ p q – 12
- 36. CS-708 Laws ofLogic – 14
- 37. CS-708 Laws ofLogic - 14a
- 38.
- 39.
- 40.
- 41.
- 42.