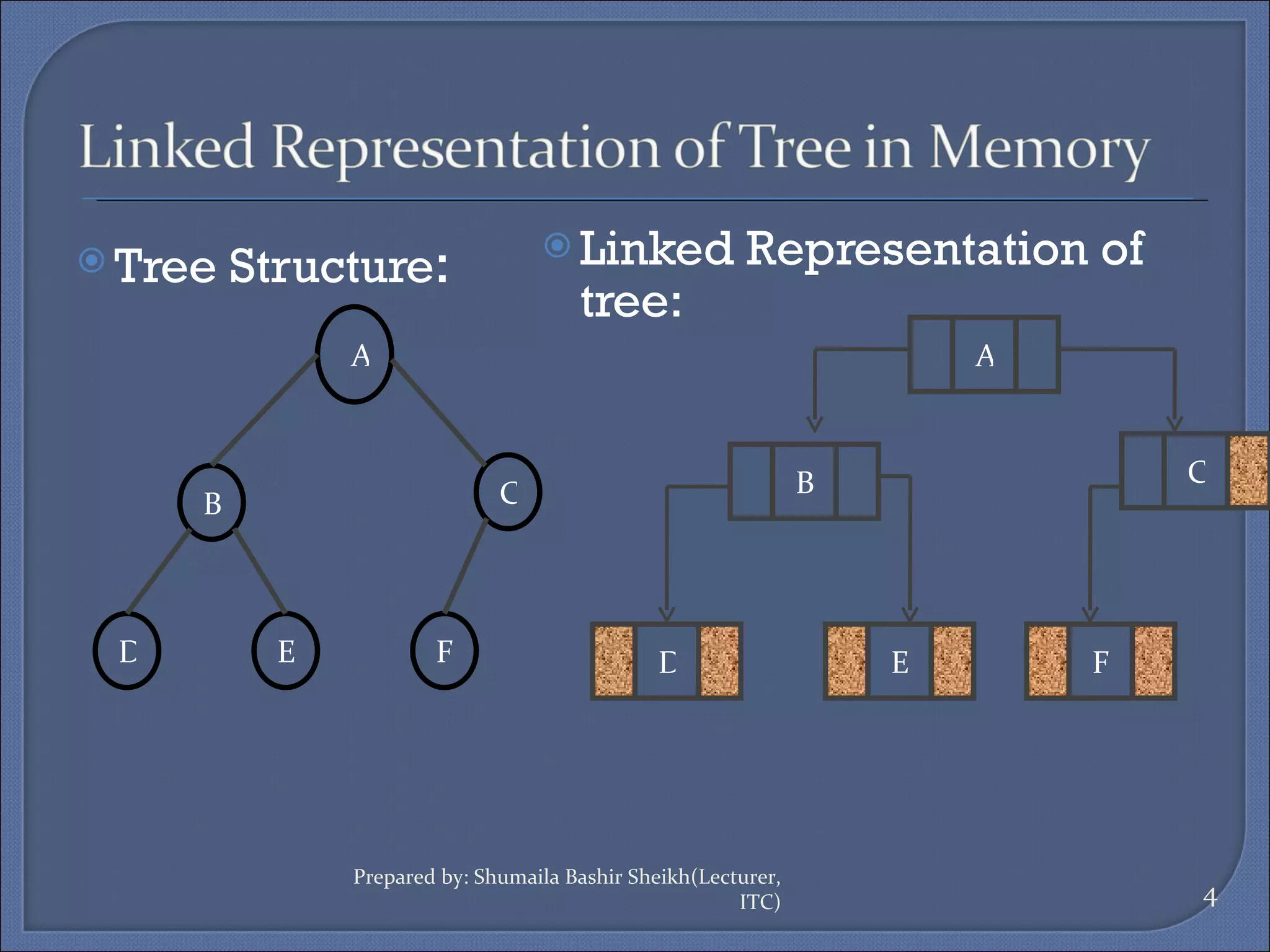
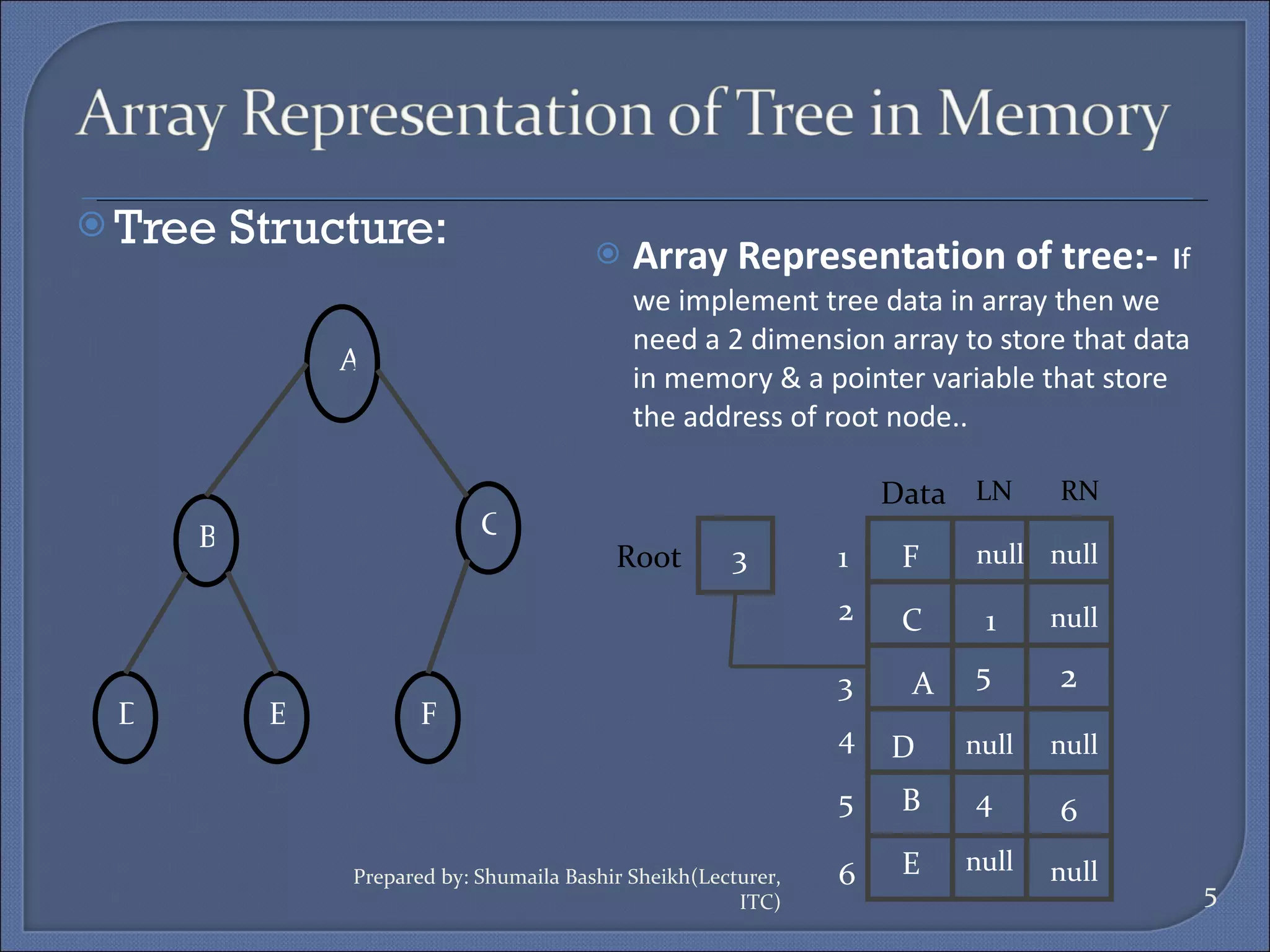
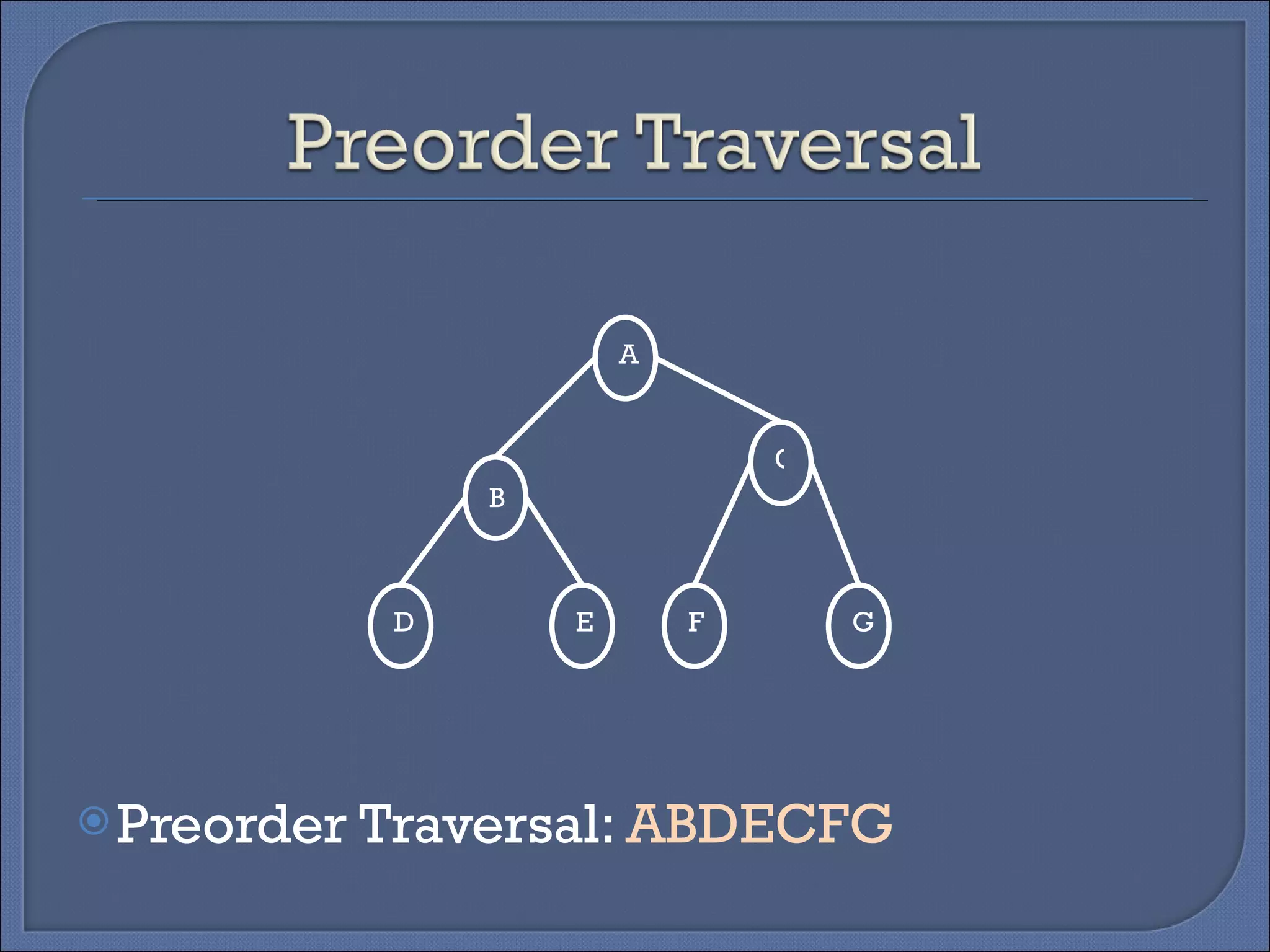
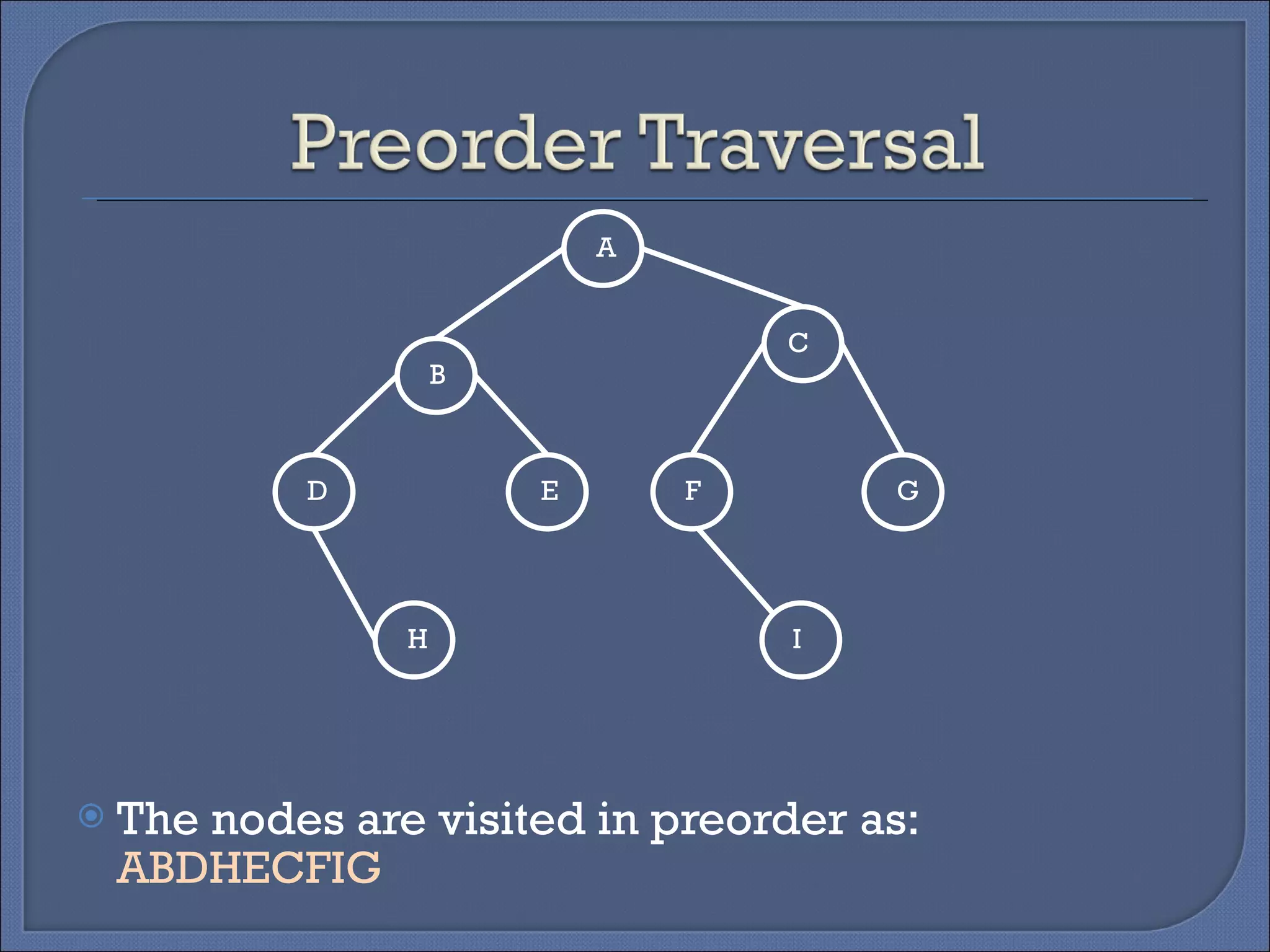
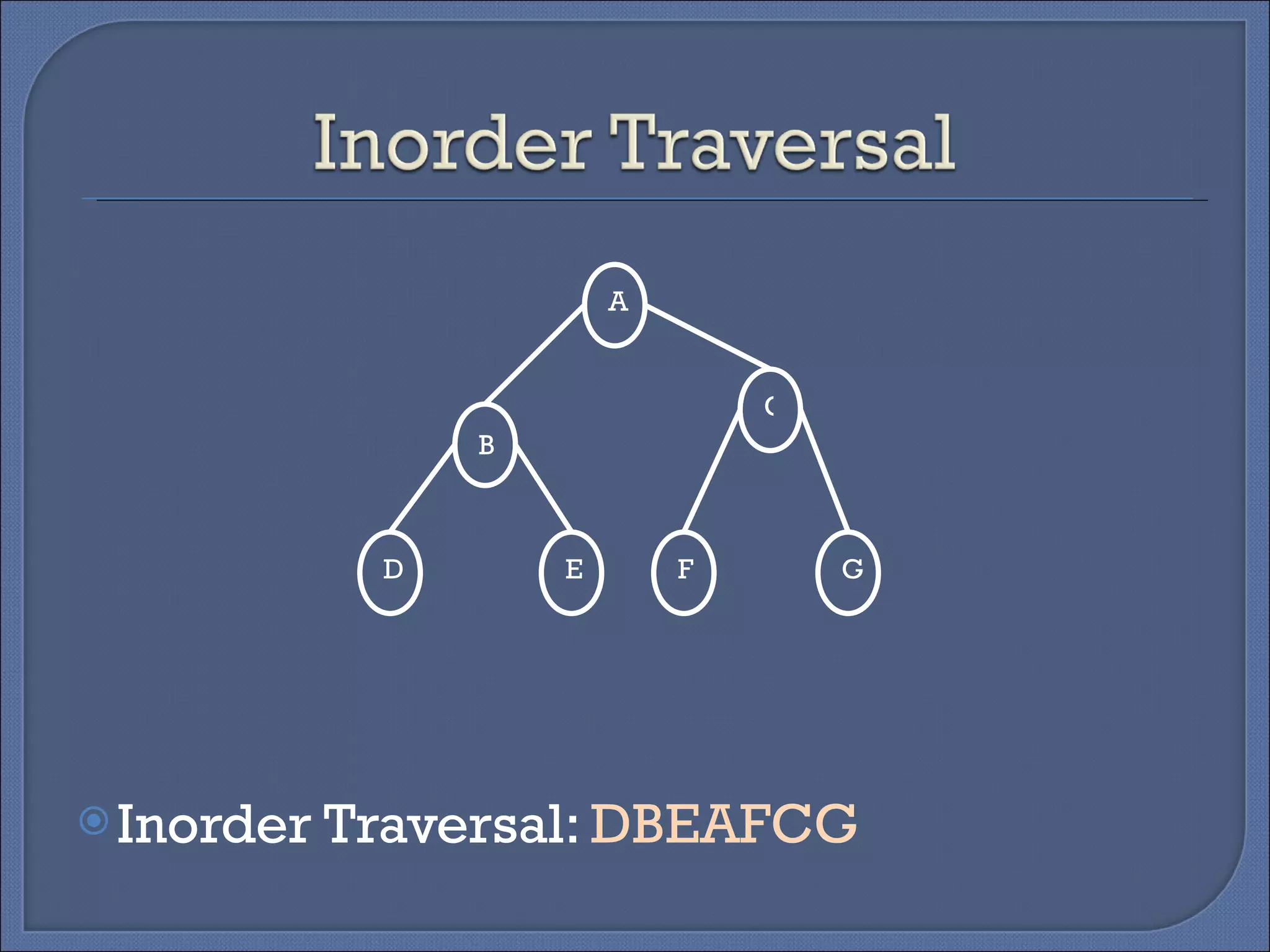
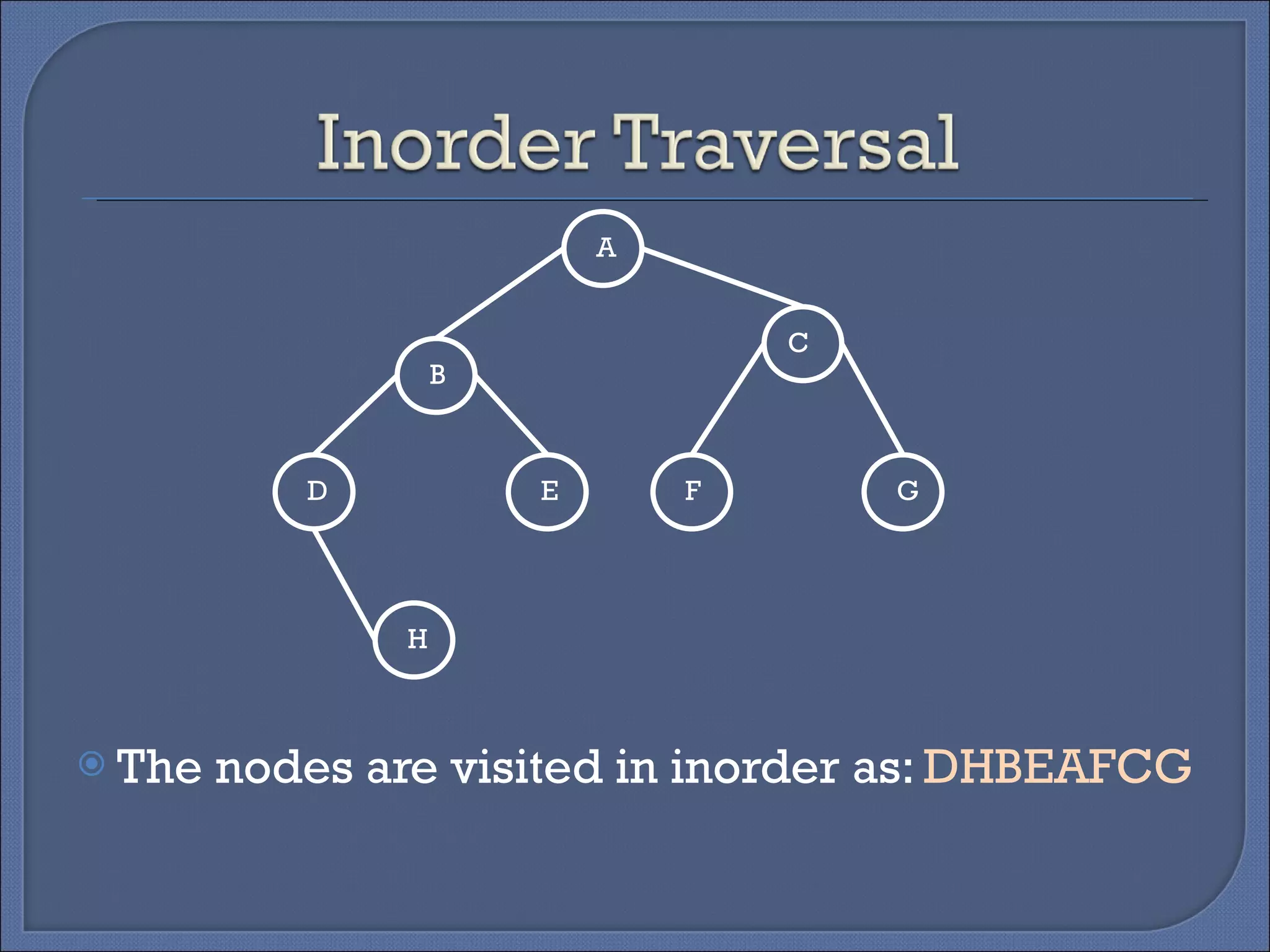
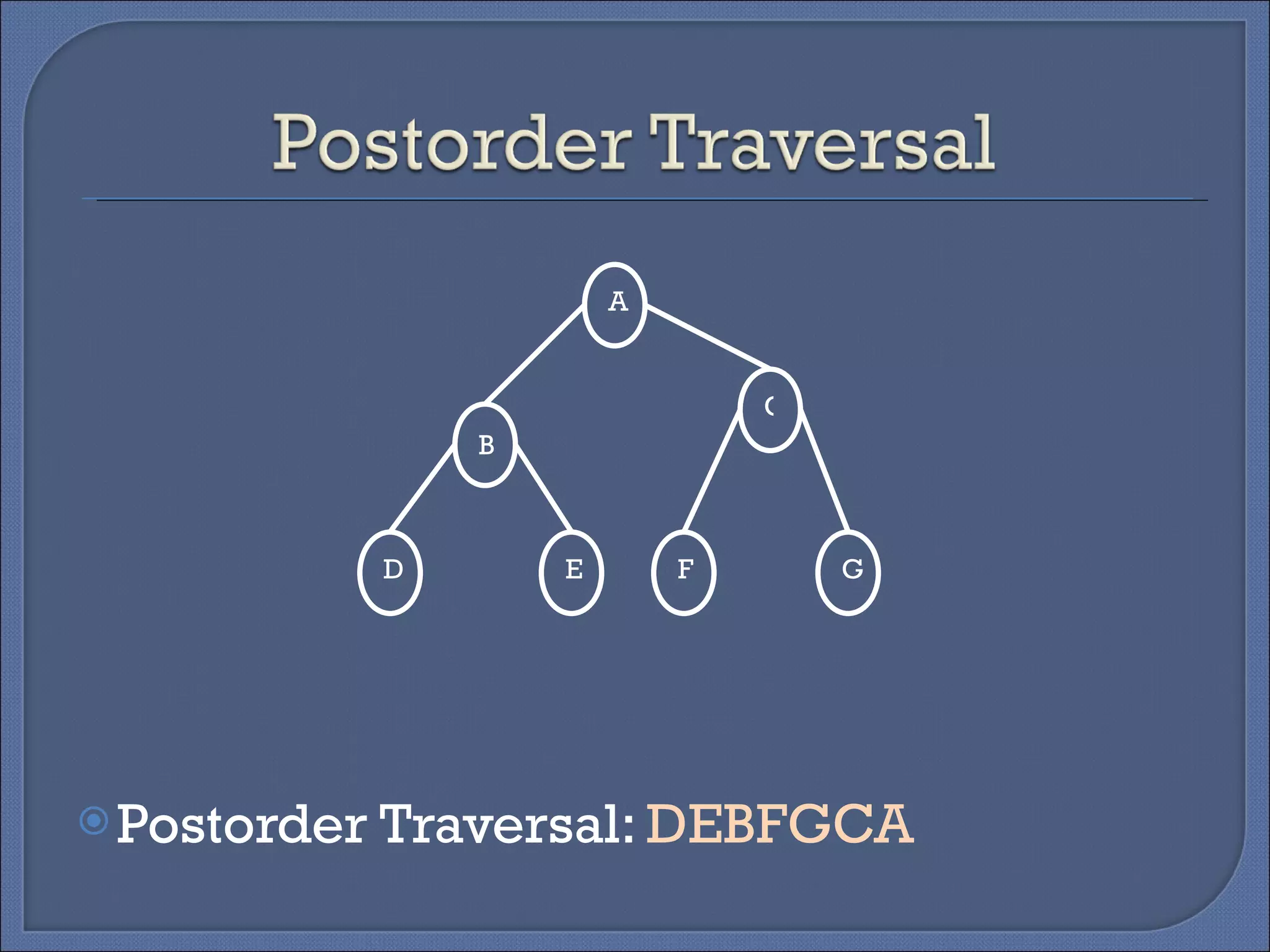
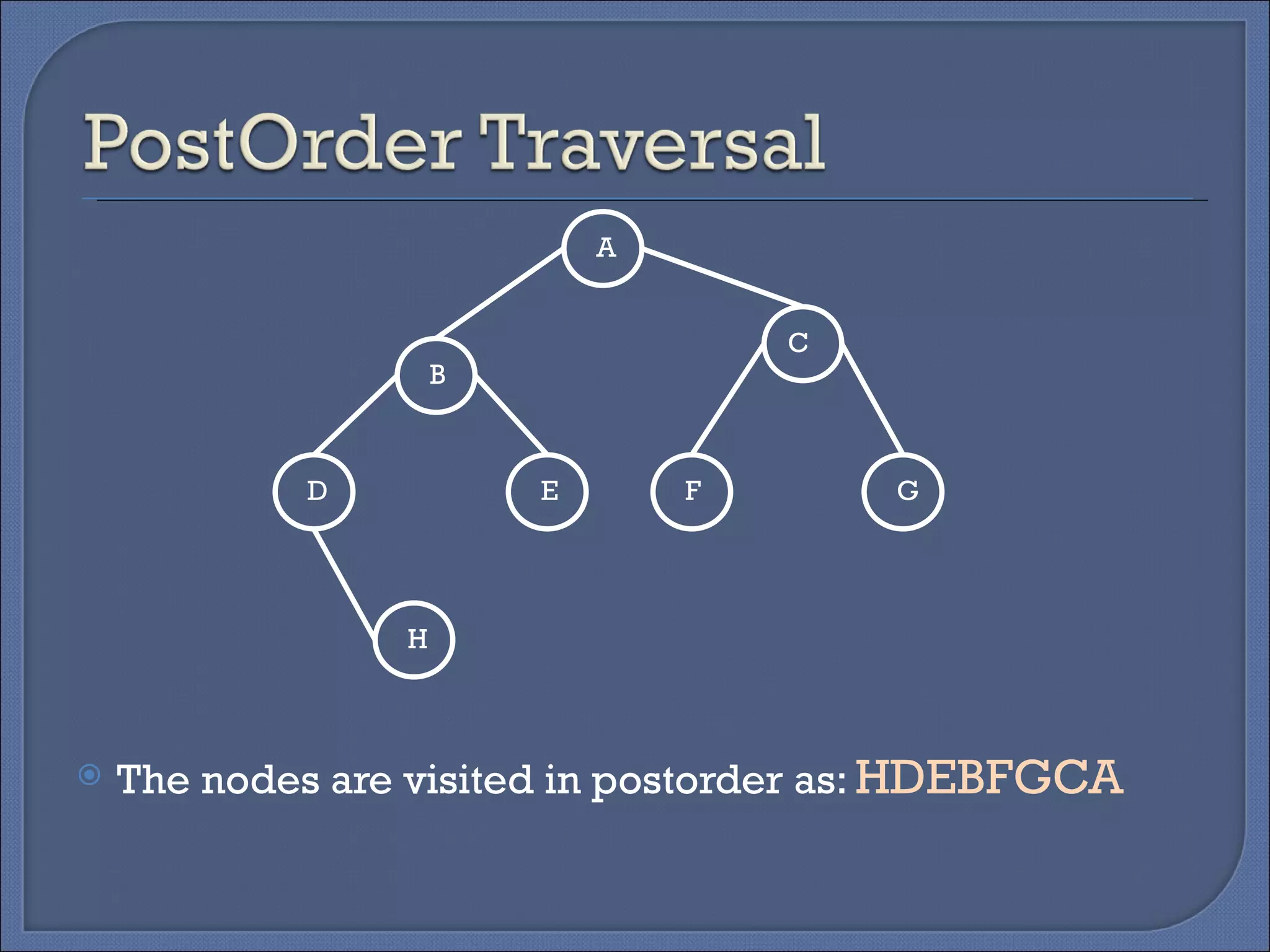
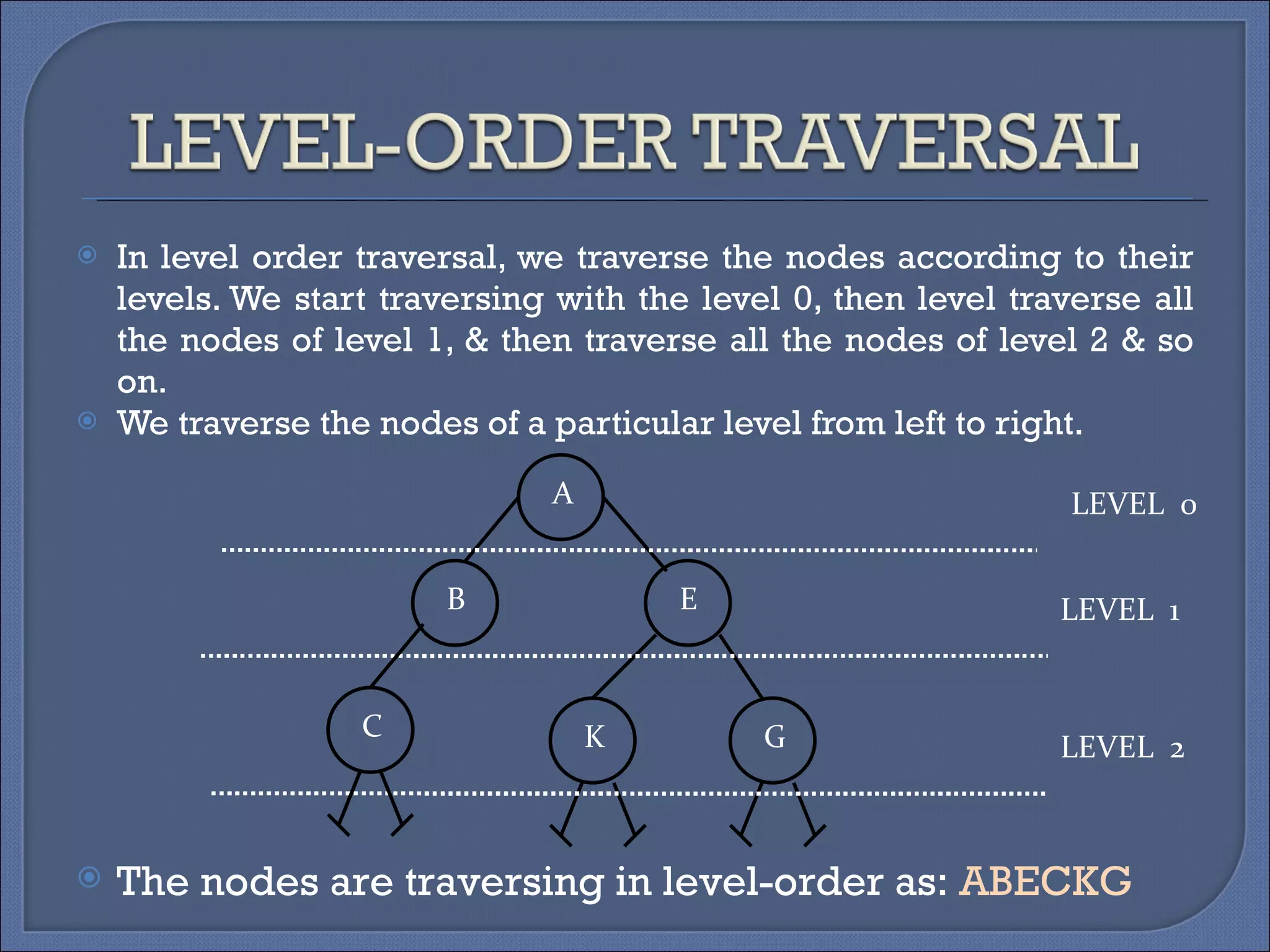
Binary trees can be implemented using two representations: linked and array. The linked representation stores each node as a structure with data, left child, and right child pointers. The array representation stores tree data in a 2D array with a root pointer variable. There are four basic tree operations: traversing, searching, inserting, and deleting. Traversing involves visiting nodes in different orders like preorder, inorder, and postorder.

1. Created by Zaheer Abbas Aghani 2k9-152

2. Non-Linear Data Structure Tree

3. As list, Stack, & Queue, binary tree can also be implement in two ways. Linked Representation Array Representation. LINKED REPRESENTATION OF BINARY TREE: if we implement tree data in linked list then every node of linked list has three member/parts. First member is for data, second and third member for left & right child . Second & third members are structure pointers which point to the same structure as for tree node. Prepared by: Shumaila Bashir Sheikh(Lecturer, ITC)

4. Tree Structure : Linked Representation of tree: A B C D E F Prepared by: Shumaila Bashir Sheikh(Lecturer, ITC) A B C D E F

5. Tree Structure: Array Representation of tree:- I f we implement tree data in array then we need a 2 dimension array to store that data in memory & a pointer variable that store the address of root node.. Data LN RN Root 3 1 2 3 4 5 6 A B D C F E 5 2 1 4 6 null null null null null null null Prepared by: Shumaila Bashir Sheikh(Lecturer, ITC) A B C D E F

6. Four Basic Operations Traversing Searching Inserting Deleting

7. In tree creation we take three parameters node, left child & right child, so traversing of binary tree means traversing of node, left subtree and right subtree. There are three standard ways to traversing a binary tree. These three algorithms are Preorder Traversal Inorder Traversal Postorder Traversal

8. Visit the root. Traverse the left subtree of root in preorder. Traverse the right subtree of root in preorder. If root is denoted as N, left subtree as L & right subtree as R then Preorder traversal is also called NLR Traversal.

9. Preorder Traversal: ABDECFG A B C D E F G

10. The nodes are visited in preorder as: ABDHECFIG I A B C D E F G H

11. Traverse the left subtree of root in Inorder. Visit the root. Traverse the right subtree of root in Inorder. Inorder traversal is also called LNR Traversal.

12. Inorder Traversal: DBEAFCG A B C D E F G

13. The nodes are visited in inorder as: DHBEAFCG A B C D E F G H

14. Traverse the left subtree in postorder. Traverse the right subtree in postorder. Visit the Root. Postorder traversal is also called LRN Traversal.

15. Postorder Traversal: DEBFGCA A B C D E F G

16. The nodes are visited in postorder as: HDEBFGCA A B C D E F G H

17. In level order traversal, we traverse the nodes according to their levels. We start traversing with the level 0, then level traverse all the nodes of level 1, & then traverse all the nodes of level 2 & so on. We traverse the nodes of a particular level from left to right. LEVEL 2 C K G The nodes are traversing in level-order as: ABECKG A E B LEVEL 0 LEVEL 1