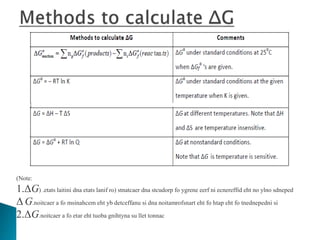
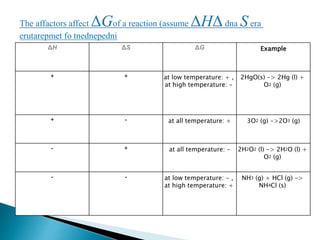
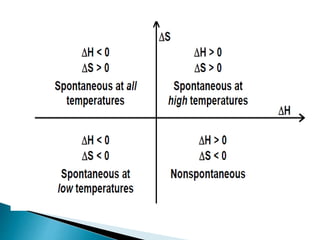
This document discusses Gibbs free energy (G) and how it relates to chemical reactions and equilibrium. It defines G and explains how it depends on enthalpy (H), entropy (S), pressure (P), and temperature (T). It describes how the change in G for a reaction (DG) determines whether the reaction is spontaneous. It shows how DG can be used to calculate equilibrium constants (K) at different temperatures and how K values change with temperature.

1. Lec.2 Gibb's Free Energy

2.  the Gibb's free energy is defined as the driving force for a
system to reach a chemical equilibrium.
 The energy comes from the enthalpy and entropy of reaction
in the system, and ΔG has been define in terms of enthalpy and
entropy changes, ΔH and ΔS, at temperature T as:
 The Gibbs Free Energy of any phase varies with pressure and
temperature. The fundamental relationship is:
G = U+ PV – TS (Eq. 1)
G = H - TS
 In the above expressions, P and T refer to pressure and
temperature. U, V, H and S refer to the internal energy,
volume, enthalpy and entropy of the phase. It follows that:
H = U + PV

3.  As above, P and T refer to pressure and temperature ΔG is the Gibbs
energy of reaction, ΔU is the internal energy of reaction, ΔV is the
volume of reaction, ΔH is the enthalpy of reaction and ΔS is the
entropy or reaction.
Look closely at Equation (1). The right hand side contains three
terms.
 The first is the change in internal energy -- a constant depending
on the phases involved.
 The second is a PV term -- it equates Gibbs Energy with volume
and pressure(FLUID WORK). More voluminous phases have
greater Gibbs Free Energy. (Recall that the energy of an ideal gas =
PV = nRT.)
 The third term involves entropy (S). Entropy is a measure of
disorder. Some phases can absorb energy simply by becoming
disordered. Temperature may not increase, volume may remain the
same, but energy disappears.

4.  ΔG =0 at equilibrium at certain T
 But when changing T the ΔG will change
 For the reaction
water liquid water vapor
ΔG =0 when there is equilibrium between the
two phases and that happen only at the boiling point
temperature at T = 373 K.
 At the room temperature where the liquid water is the
only phase present ΔG =8.59 at T = 298 K(25 ºC)

5.  So what is special for any reaction at the boiling point ?
 The answer is at boiling point there is equilibrium
between vapor and liquid phases and ΔG =0
• Chemical systems seek to minimize energy and,
consequently, phases of greater Gibbs Free
Energy are unstable with regard to phases with
lower Gibbs Free Energy.
• In terms of Δ G:
– If Δ G < 0…..process is spontaneous(-ve)
– If Δ G > 0…..process is spontaneous in opposite direction(+ve)
– If Δ G = 0….equilibrium

7.  Note that DG is composite of both DH and DS
DG = DH – TDS
A reaction is spontaneous if ΔG < 0. Such that:
 If ΔH < 0 and ΔS > 0….spontaneous at all T
 If ΔH > 0 and ΔS < 0….not spontaneous at all T
 If ΔH < 0 and ΔS < 0….spontaneous at low T
 If ΔH > 0 and ΔS > 0….spontaneous at high T

9.  At what T is the following reaction
spontaneous?
Br2(l) Br2(g)
where DH° = 30.91 kJ/mol,
DS° = 93.2 J/mol.K
• Ans: DG° = DH° - TDS°

10.  Try 298 K just to see:
DG° = DH° - TDS°
DG° = 30.91 kJ/mol - (298K)(93.2 J/mol.K)
DG° = (30.91 - 27.78) kJ/mol
= 3.13 kJ/mol > 0
Not spontaneous at 298 K

11.  At what T then?
DG° = DH° - TDS°
T = DH/DS
T = (30.91 kJ/mol) /(93.2 J/mol.K) *103
= 0
Just take care of units
T = 331.65 K
(kJ to J)

12. standard free energy of formation (ΔG°f ) of a substance
it is the free-energy change for the formation of 1 mole of the
substance from its elements in their standard states,
– Thus, the ΔG°f of a substance is a measure of its thermodynamic
stability with respect to its constituent elements.
– Substances with negative values for ΔG°f are stable and do not
decompose into their constituent elements.
– e.g. water’s: ΔG°f =-237.2 kJ/mol
while CO2’s ΔG°f =-394.4 kJ/mol

13.  In our previous example, we needed to determine
ΔH°rxn and Δ S°rxn to determine Δ G°rxn
• Now, Δ G is a state function; therefore, we
can use known Δ G° to determine Δ G°rxn
using:
DGrxn = DGprod. -
 DGreact.


14. standard free energy change (ΔG°)
it is the free-energy change for a reaction when the reactants
in their standard states are converted to the products in their
standard states.
→ Thus, we can use a table of standard free energy of
formation values (ΔG°f ) for reactants and products to
calculate standard free energy changes (ΔG°) for various
chemical reactions, just like we did for ΔH° and ΔS°.
Thus, the standard free energy change (ΔG°) can be
calculated as:

15.  Determine the DG°rxn for the following:
C2H4(g) + H2O(l) C2H5OH(l)
• Tabulated DG°f :
DG°f(C2H5OH(l)) = -175 kJ/mol
DG°f(C2H4(g)) = 68 kJ/mol
DG°f(H2O (l)) = -237 kJ/mol

16.  Using these values:
C2H4(g) + H2O(l) C2H5OH(l)
DG°rxn = DG°f(C2H5OH(l)) - DG°f(C2H4(g))
-DG°f(H2O (l))
DGrxn = DGprod. -
 DGreact.

DG°rxn = -175 kJ - 68 kJ -(-237 kJ)
DG°rxn = -6 kJ < 0 ; therefore, spontaneous
Why is it spontaneous and for what temperatures is this true?
ΔH°rxn =-44kJ; from this get ΔS°rxn =-120J/K.
Spontaneous at low T

17. Important notes:
Remember that ΔH results from bonds being broken and made in
chemical reactions.
– The ΔG part can be used for motion, light, heat, etc.—ie., to do
useful work.
→ Why ΔG is called free energy ?,-------
It is considered the energy to do useful work.
– However, keep in mind that the work obtained from ΔG is never
100% efficient.
– Next, the TΔS part is the temperature-dependent change in
entropy, that part of the energy change that simply increases the
entropy of the universe.

18. Gibbs Free Energy and Chemical Equilibrium
The standard free energy change (ΔG°) only applies to standard
state conditions, where temperature is 25°C and all gas pressures are
1 atm.
→ Thus, ΔG° only allows us to predict if a reaction is spontaneous
at these conditions.
However, many reactions do not occur at these conditions.
→ A more general free energy change at nonstandard conditions
(ΔG) allows us to predict if a reaction/process is spontaneous for all
other conditions:

19. R is the gas constant (8.314 J/K•mol)
T is the absolute temperature (K)
Q is the reaction quotient = [Products]0 or P°Products
18.4
So we Can correct Gibbs Free Energy change for non-
standard state
[Reactants]0 P°Reactants
Q=reaction quotient indicating the state of a system at a given instant.
Conc.
Pressure

20. The General Case
Here, we will: (1) Use activities, rather than pressures
(2) Consider a more general reaction
aA + bB  cC + dD
A = A
o + RT•ln(aA)
B = B
o + RT•ln(aB)
DrG = {cC + dD} - {aA + bB}
DrG = DrGo + RT•ln(Q)
C = C
o + RT•ln(aC)
D = D
o + RT•ln(aD)
c d
C D
a b
A B
a a
Q
a a
=
It can be shown that:

22. Gibbs Free Energy and Chemical Equilibrium
DG = DG0 + RT lnQ
R is the gas constant (8.314 J/K•mol)
T is the absolute temperature (K)
Q is the reaction quotient
At Equilibrium
DG = 0 Q = K
0 = DG0 + RT lnK
DG0 = - RT lnK

23. N2 (g) + 3H2 (g) 2 NH3 (g)
What is Kp for the following reaction at 25 0C, DG0=33.32 KJ ?
Kp = e
-DG0 / RT
Kp = e
- (-33.32 kJ)/(0.008314 kJ /molK)(298K)
Kp = e
13.4
Kp = 6.6 x 105

24. 2 NO (g) + O2 (g) 2 NO2 (g)
Calculate DG0 for the following reaction at 25 0C?
Given:
DH° S°
NO 90.37 kJ/mole 210.62 j/molK
O2 0 205.0
NO2 33.84 240.45
DG0 = DH0 – TDS0
DS0
rxn
= 2 x S0(NO2) – [2 x S0(NO) – S0(O2)]
DH0
rxn
= 2 x DH0(NO2) – [2 x DH0(NO) + DH0(O2)]
f
f f f
= 2(33.84 kJ) - 2(90.37 kJ) - 0 = -113.06 kJ
= 2(240.45J/molK) - 2(210.62 J/molK) - 205.0 j/molK
= -145.34 J/K

25. DG0 = DH0 – TDS0
DG0
rxn
= 2 x DG0(NO2) – [2 x DG0(NO) + DG0(O2)]
f f
f
= 2(51.84 kJ/mol) - 2(86.71 kJ/mol) - 0
= 103.68 kJ - 173.42 kJ
= -69.74 kJ
= -113.06 kJ - (298 K)(- 0.14534 kJ/K
= -113.06 kJ + 43.31 kJ = -69.75 kJ
Can also calculate with DG0 ’s from tabulated data
f

27. (Note:
1.ΔG etats laitini dna etats lanif ro( stnatcaer dna stcudorp fo ygrene eerf ni ecnereffid eht no ylno sdneped
.
(
Δ Gnoitcaer a fo msinahcem eht yb detceffanu si dna noitamrofsnart eht fo htap eht fo tnednepedni si
.
2.ΔGnoitcaer a fo etar eht tuoba gnihtyna su llet tonnac
.

28. ΔH ΔS ΔG Example
+ + at low temperature: + ,
at high temperature: -
2HgO(s) -> 2Hg (l) +
O2 (g)
+ - at all temperature: + 3O2 (g) ->2O3 (g)
- + at all temperature: - 2H2O2 (l) -> 2H2O (l) +
O2 (g)
- - at low temperature: - ,
at high temperature: +
NH3 (g) + HCl (g) ->
NH4Cl (s)
The affactors affect ΔGof a reaction (assume ΔH dna
Δ Sera
erutarepmet fo tnednepedni

29. - RT lnK = DG0 = DH0 – TDS0
How does K change with Temperature?
At equilibrium:
RT lnK + DH0 = TDS0
R lnK + DH0/T = DS0
constant
Compare 2 Temperatures:
R lnK1 + DH0/T1 = R lnK2 + DH0/T2
R(lnK2 - lnK1) = DH0/T1 - DH0/T2
ln(K2 / K1) = DH0/R (1/T1 - 1/T2)

30. H2 (g) + I2 (g) 2 HI (g)
What is Kp for the following reaction at 25 0C?
Kp = e
-DG0 / RT - (2.6 kJ)/(0.008314 kJ /molK)(298K) -1.05
Kp = 0.350
DG0 = 2.6 kJ
= e = e
What is Kp at 50 0C?
DH0
rxn
= 2(25.9 kJ/mole) – 0 – 0 = 51.8 kJ
ln(K2 / K1) = DH0/R (1/T1 + 1/T2)
ln(K2 / 0.350 = (51.8 kJ )/(0.008314 kJ /molK)(1/298K + 1/323K)
lnK2 - ln0.350 = (6.23 x 103)(2.60 x 10-4)
lnK2 = 1.62 - 1.05 = 0.60
K2 = 1.82