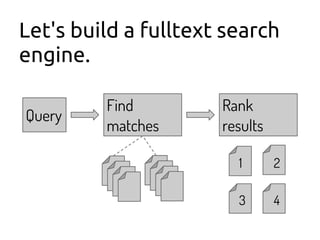
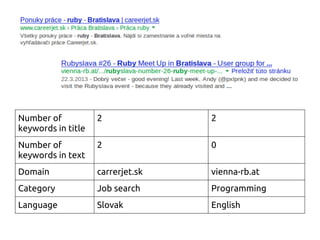
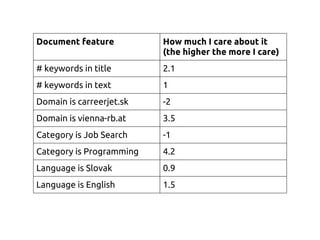
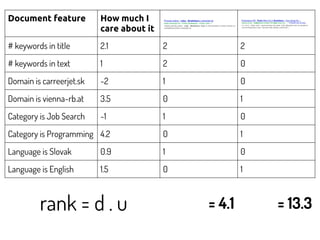
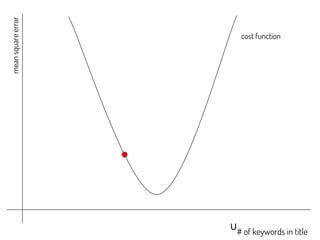
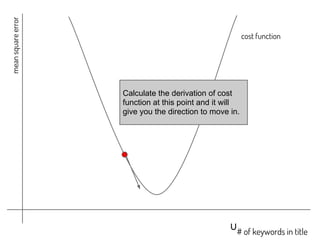
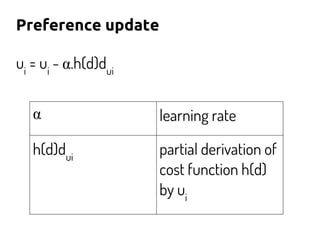
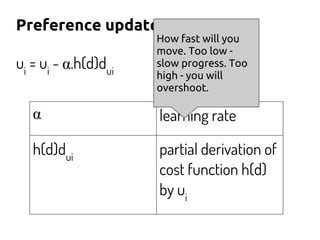
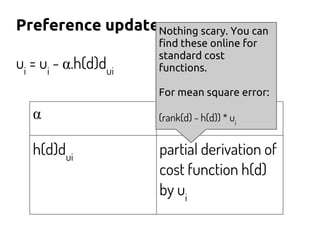
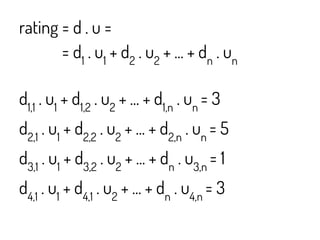The document discusses using machine learning and gradient descent to learn user preferences for ranking search results based on clicks. It proposes using gradient descent to adjust user preference weights to minimize the error between estimated rankings produced by a preference-based ranking function and actual user clicks. Preference weights are updated on each iteration by moving in the direction that reduces the cost function, which is initially mean squared error but later proposed to be based on pairwise document comparisons to account for implicit feedback from clicks alone.

1. Learning to rank
fulltext results from
clicks
Tomáš Kramár
@tkramar
@synopsitv

2. Let's build a fulltext search
engine.
Query
Find
matches
Rank
results
1 2
43

3. Let's build a fulltext search
engine.
Query
Find
matches
Rank
results
1 2
43
● ElasticSearch
● LIKE %%
● ...

4. Let's build a fulltext search
engine.
Query
Find
matches
Rank
results
1 2
43
● By number of hits
● By PageRank
● By Date
● ...

6. How do
you
choose
relevant
results?

7. Number of
keywords in title
2 2
Number of
keywords in text
2 0
Domain carrerjet.sk vienna-rb.at
Category Job search Programming
Language Slovak English

8. Document feature How much I care about it
(the higher the more I care)
# keywords in title 2.1
# keywords in text 1
Domain is carreerjet.sk -2
Domain is vienna-rb.at 3.5
Category is Job Search -1
Category is Programming 4.2
Language is Slovak 0.9
Language is English 1.5

9. Document feature How much I
care about it
# keywords in title 2.1 2 2
# keywords in text 1 2 0
Domain is carreerjet.sk -2 1 0
Domain is vienna-rb.at 3.5 0 1
Category is Job Search -1 1 0
Category is Programming 4.2 0 1
Language is Slovak 0.9 1 0
Language is English 1.5 0 1
= 4.1 = 13.3rank = d . u

10. Rate each
result on
a scale 1-
5.

11. rating = d . u =
= d1
. u1
+ d2
. u2
+ ... + dn
. un
d1,1
. u1
+ d1,2
. u2
+ ... + d1,n
. un
= 3
d2,1
. u1
+ d2,2
. u2
+ ... + d2,n
. un
= 5
d3,1
. u1
+ d3,2
. u2
+ ... + dn
. u3,n
= 1
d4,1
. u1
+ d4,1
. u2
+ ... + dn
. u4,n
= 3

12. rating = d . u =
= d1
. u1
+ d2
. u2
+ ... + dn
. un
d1,1
. u1
+ d1,2
. u2
+ ... + d1,n
. un
= 3
d2,1
. u1
+ d2,2
. u2
+ ... + d2,n
. un
= 5
d3,1
. u1
+ d3,2
. u2
+ ... + dn
. u3,n
= 1
d4,1
. u1
+ d4,1
. u2
+ ... + dn
. u4,n
= 3
di,j
are known, solve this system of
equations and you have u. Done.

13. Except..
● You don't know the explicit
ratings
● User preferences change in time
● Those equations probably don't
have solution

14. Clicked!
Assume
rating 1.
Not clicked.
Assume
rating 0.

15. Except..
● You don't know the explicit
ratings
● User preferences change in time
● Those equations probably don't
have solution

16. Approximation function
h(d): d → rank
h(d) = d1
.u1
+ ... + dn
.un
= estimated_rank
If the function is good, it should make
minimal errors
error = (estimated_rank - real_rank)2

17. Gradient descent
1. Set user preferences (u) to arbitrary
values
2. Calculate the estimated rank h(d)
for each document
3. Calculate the mean square error
4. Adjust preferences u in a way that
minimizes the error
5. Repeat until the error converges

18. meansquareerror
u# of keywords in title
cost function

19. meansquareerror
u# of keywords in title
cost function
Calculate the derivation of cost
function at this point and it will
give you the direction to move in.

20. Preference update
ui
= ui
- α.h(d)dui
α learning rate
h(d)dui
partial derivation of
cost function h(d)
by ui

21. Preference update
ui
= ui
- α.h(d)dui
α learning rate
h(d)dui
partial derivation of
cost function h(d)
by ui
How fast will you
move. Too low -
slow progress. Too
high - you will
overshoot.

22. Preference update
ui
= ui
- α.h(d)dui
α learning rate
h(d)dui
partial derivation of
cost function h(d)
by ui
Nothing scary. You can
find these online for
standard cost
functions.
For mean square error:
(rank(d) - h(d)) * ui

23. Gradient descent
1. Set user preferences (u) to arbitrary
values
2. Calculate the estimated rank h(d)
for each document
3. Calculate the square error
4. Adjust preferences u in a way that
minimizes the error
5. Repeat until the error converges

24. Clicked! Assume
rating 1.
Clicked! Assume
rating 1.
Or? Doesn't
this mean
result #1 is not
relevant?

25. Clicked! Assume
nothing.
Clicked! Assume
it is better than
#2 and #3.

26. What's changed?
We no longer have ratings, just document
comparisons.
Cost function - something that
considers ordering, e.g., Kendall's T
(number of concordant and
discordant pairs)
h is now a function of 2
parameters: h(d1, d2). But you can
just do d2 - d1 and learn on that.
d4
> d3
d4
> d2