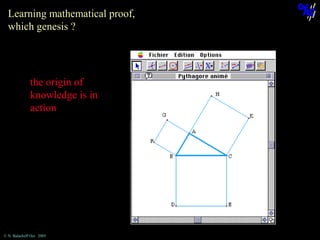
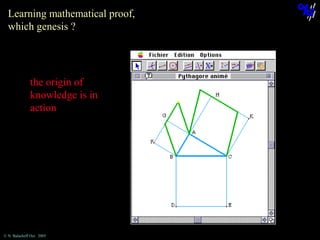
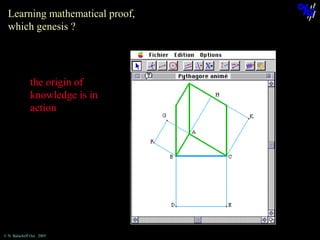
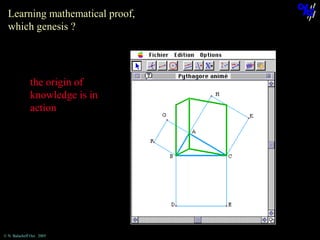
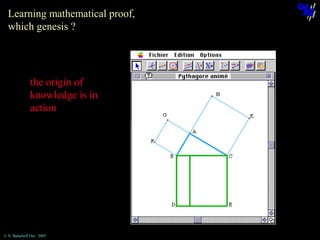
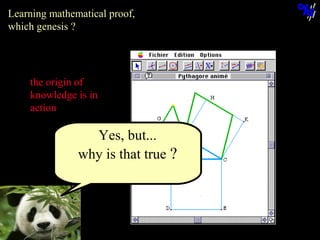
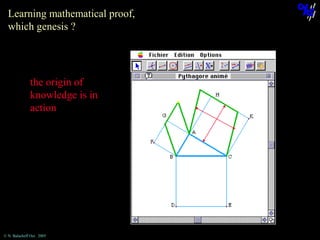
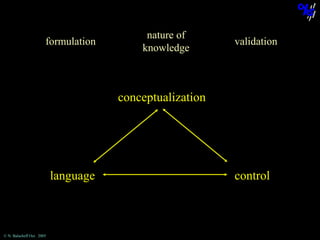
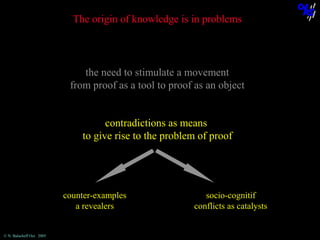
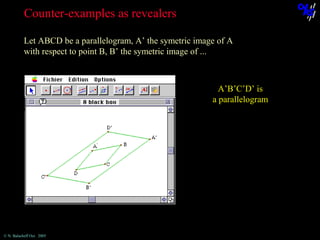
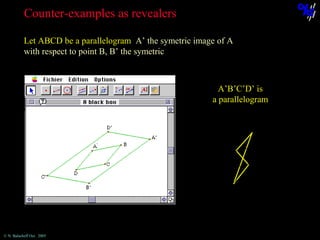
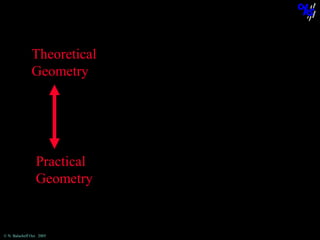
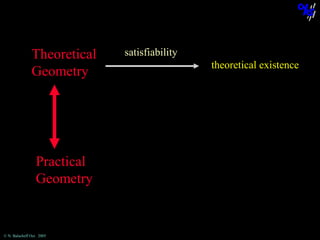
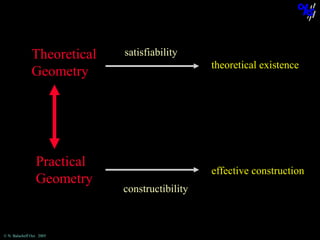
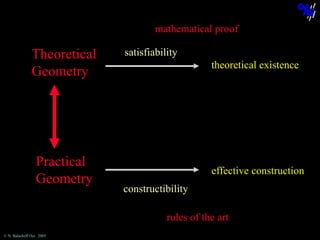
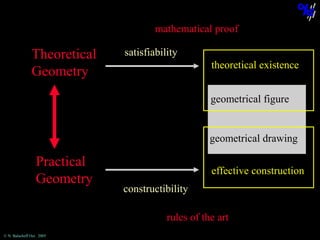
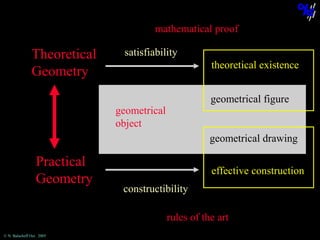
The document discusses learning mathematical proof and the genesis of knowledge. It argues that the origin of knowledge is in action, through problem solving, but achieving mathematical proof requires language. Effective learning involves a progression from knowledge in action to knowledge expressed through discourse. Computer-based environments that allow interaction with mathematical objects can help bridge this gap by providing a virtual reality for abstract concepts.































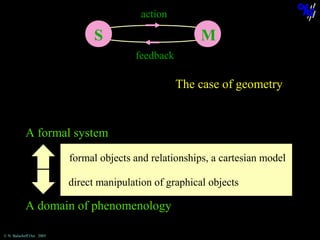
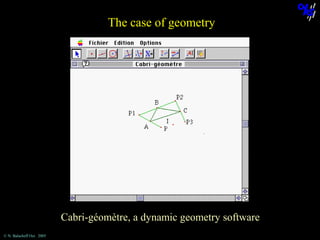
![The case of geometry
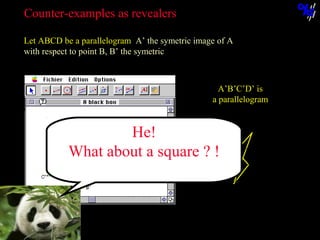
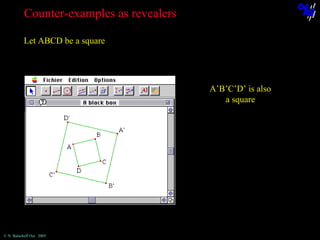
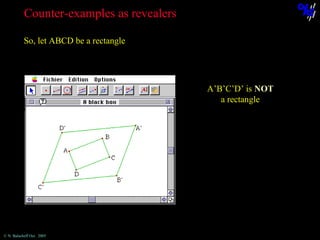
Construct the symmetrical point P1 of P about A,
then the symmetrical point P2 of P1 about B, etc.
Then, construct the point I, the midpoint of [PP3].
What can be said about the point I when P is moved?
Cabri-géomètre, a dynamic geometry software
© N. Balacheff Oct. 2005](https://image.slidesharecdn.com/sdsuseminar2005-131208125754-phpapp02/85/Learning-mathematical-proof-lessons-learned-and-outlines-of-a-learning-environment-52-320.jpg)




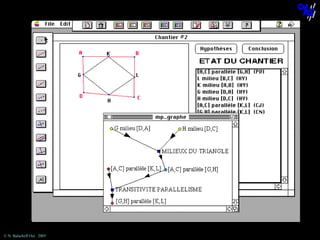
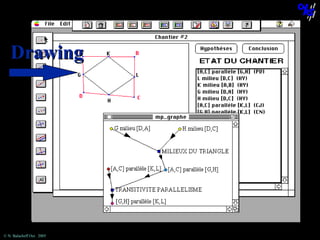
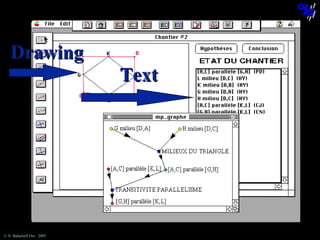
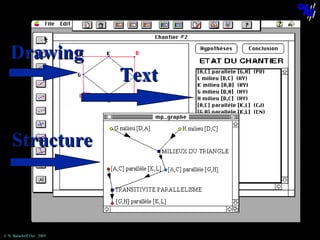
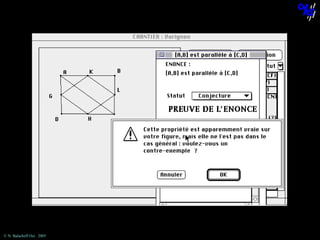
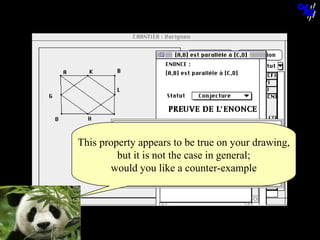
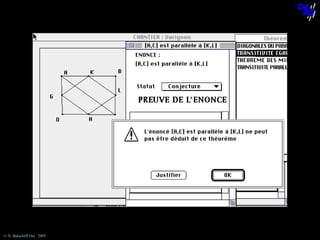
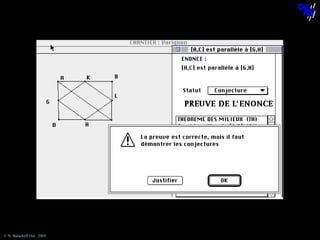
![The statement “[AC] is parallel to [KL]”
cannot be obtained using this theorem.
© N. Balacheff Oct. 2005](https://image.slidesharecdn.com/sdsuseminar2005-131208125754-phpapp02/85/Learning-mathematical-proof-lessons-learned-and-outlines-of-a-learning-environment-70-320.jpg)