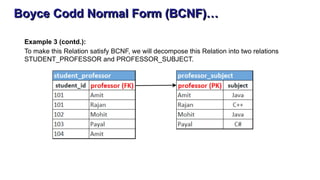
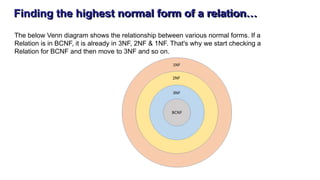
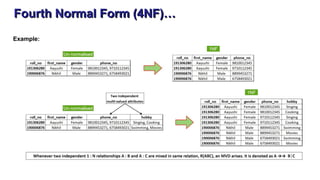
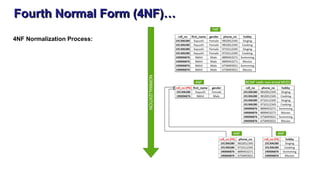
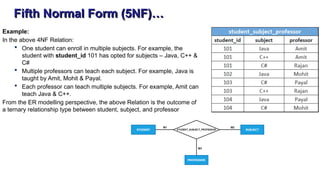
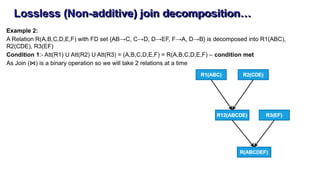
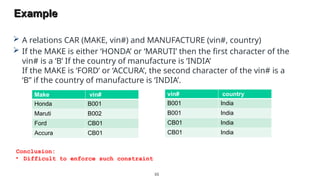
The document discusses the process of normalization in database design, specifically focusing on the first (1NF), second (2NF), and third normal forms (3NF), along with Boyce-Codd Normal Form (BCNF). It elaborates on the definitions, conditions, and examples of each form to eliminate data redundancy and anomalies. Each section provides methods for converting between the forms to ensure efficient and effective database structure.