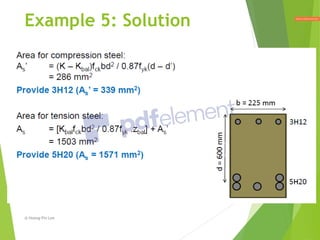
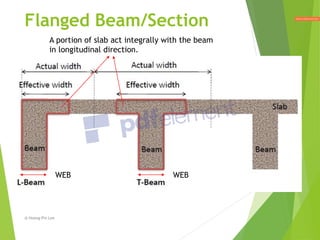
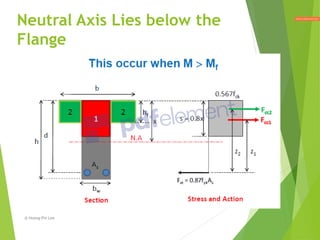
This document provides an overview of moment design and flexure design procedures for reinforced concrete structures. It discusses design and checking of singly and doubly reinforced rectangular and flanged sections subjected to bending. Key steps covered include determining the neutral axis depth, tension and compression reinforcement requirements, and checking moment capacity. Design examples are provided to illustrate the application of these procedures to different section types and load cases.

1. CHAPTER 2 MOMENT DESIGN /
FLEXURE DESIGN
@ Hoong-Pin Lee

2. @ Hoong-Pin Lee

3. DESIGN METHOD / PROCEDURES
Based on Section 6.1 MS EN 1992-1-1 – ULS analysis
and design of section subjected to bending
@ Hoong-Pin Lee

4. In this chapter, you’ll learn
about:
 Rectangular section: Singly and doubly
reinforced
 Flanged section: Singly and doubly
reinforced
@ Hoong-Pin Lee

5. Two different types of problems
in the study of RC flexural
elements:
 (1) Design:
 Given a cross-section, concrete strength, steel
reinforcement strength, and applied ultimate bending
moment, determine the area and number of
reinforcement required.
 (2) Design Check:
 Given a cross-section, concrete strength, number, strength
and size of steel reinforcement provided, determine the
moment of resistance.
@ Hoong-Pin Lee

6. Which one is T, L, & Rectangular?
@ Hoong-Pin Lee

7. Stress Block Diagram
S = 0.8x
𝑓𝑐𝑑 = 0.567𝑓𝑐𝑘
𝜇 = 1.0
Lecture 1, slide 35
𝑓𝑦𝑑 = 0.87𝑓𝑦𝑘
Lecture 1, slide 38
@ Hoong-Pin Lee

8. Singly Reinforced Section
Stress Area
@ Hoong-Pin Lee

9. Singly Reinforced Section
@ Hoong-Pin Lee

10. Singly Reinforced Section
(to avoid sudden failure)
@ Hoong-Pin Lee

11. Singly Reinforced Section
@ Hoong-Pin Lee

12. Example 1
@ Hoong-Pin Lee

13. Example 1: Solution
@ Hoong-Pin Lee

14. Example 1: Solution
@ Hoong-Pin Lee

15. Example 2
@ Hoong-Pin Lee

16. Example 2: Solution
@ Hoong-Pin Lee

17. Example 2: Solution
@ Hoong-Pin Lee

18. Doubly Reinforced Section
@ Hoong-Pin Lee

19. Doubly Reinforced Section
@ Hoong-Pin Lee

20. Doubly Reinforced Section
@ Hoong-Pin Lee

21. Doubly Reinforced Section
@ Hoong-Pin Lee

22. Doubly Reinforced Section
Stress in Compression Reinforcement
@ Hoong-Pin Lee

23. Doubly Reinforced Section
Stress in Compression Reinforcement
(a reduced stress should be used)
Reduced stress formula
@ Hoong-Pin Lee

24. Doubly Reinforced Section
Stress in Compression Reinforcement
@ Hoong-Pin Lee

25. Example 3
@ Hoong-Pin Lee

26. Example 3: Solution
@ Hoong-Pin Lee

27. Example 3: Solution
@ Hoong-Pin Lee

28. Example 3: Solution
@ Hoong-Pin Lee

29. Example 4
@ Hoong-Pin Lee

30. Example 4: Solution
@ Hoong-Pin Lee

31. Example 4: Solution
@ Hoong-Pin Lee

32.  The plastic behavior of reinforced concrete at the ULS affects
the distribution of moments in a structure.
 To allow for this, the moment derived from an elastic analysis
may be redistributed based on the assumption that plastic
hinges have formed at the sections with the largest moments.
 Formation of plastic hinges required relatively large rotations
with yielding of the tension reinforcement.
 To ensure large strain in the tension steel, the code of practice
restricts the depth of the neutral axis to correspond with the
magnitude of the moment redistribution carried out.
Moment REDistribution
@ Hoong-Pin Lee

33. Plastic Hinges
@ Hoong-Pin Lee

34. Moment Distribution
@ Hoong-Pin Lee

35. Moment Distribution
@ Hoong-Pin Lee

36. Moment Distribution
Prove this equation!
@ Hoong-Pin Lee

37. Moment Distribution
@ Hoong-Pin Lee

38. Derivation of z Equation
(S = 0.8x)
@ Hoong-Pin Lee

39. Simplified EC2 Method
@ Hoong-Pin Lee

40. Simplified EC2 Method
@ Hoong-Pin Lee

41. Simplified EC2 Method
@ Hoong-Pin Lee

42. Example 5
@ Hoong-Pin Lee

43. Example 5: Solution
@ Hoong-Pin Lee

44. Example 5: Solution
@ Hoong-Pin Lee

45. Example 5: Solution
@ Hoong-Pin Lee

46. Flanged Beam/Section
A portion of slab act integrally with the beam
in longitudinal direction.
WEB
WEB
@ Hoong-Pin Lee

47.  When the flange is relatively wide, the flexural
compressive stress is not uniform over its width.
 The stress varies from a maximum in the web region to
progressively lower values at points farther away from
the web.
 In order to operate within the framework of the theory
of flexural, which assumes a uniform stress distribution
across the width of the section,
 IT IS NECESSARY TO DEFINE AN EFFECTIVE FLANGE
WIDTH
Flanged Beam/Section
@ Hoong-Pin Lee

48. Flanged Beam
Cl 5.3.2.1 (EC2)
@ Hoong-Pin Lee

49. How to determine 𝒃𝒆𝒇𝒇?
@ Hoong-Pin Lee

50. How to determine 𝒃𝒆𝒇𝒇?
@ Hoong-Pin Lee

51. Design Consideration
@ Hoong-Pin Lee

52. Neutral Axis Lies in the Flange
Note: All the concrete on the tension side is assumed
ineffective in flexural computations, and the flanged
beam may just as well be treated as a rectangular section
having a width 𝑏𝑒𝑓𝑓.
@ Hoong-Pin Lee

53. Neutral Axis Lies in the Flange
(Maximum Case)
@ Hoong-Pin Lee

54. Example 6
@ Hoong-Pin Lee

55. Example 6: Solution
@ Hoong-Pin Lee

56. Example 6: Solution
@ Hoong-Pin Lee

57. Design Consideration
@ Hoong-Pin Lee

58. Neutral Axis Lies below the
Flange
@ Hoong-Pin Lee

59. Neutral Axis Lies below the
Flange
(Take moment @ steel reinforcement)
@ Hoong-Pin Lee

60. Neutral Axis Lies below the
Flange
@ Hoong-Pin Lee

61. Neutral Axis Lies below the
Flange
@ Hoong-Pin Lee

62. Example 7
@ Hoong-Pin Lee

63. Example 7: Solution
@ Hoong-Pin Lee

64. Example 7: Solution
@ Hoong-Pin Lee

65. Example 7: Solution
@ Hoong-Pin Lee

66. Design Consideration
@ Hoong-Pin Lee

67. Neutral Axis Lies below the
Flange (M>𝑴𝒃𝒂𝒍 )
@ Hoong-Pin Lee

68. Neutral Axis Lies below the
Flange (M>𝑴𝒃𝒂𝒍 )
@ Hoong-Pin Lee

69. Neutral Axis Lies below the
Flange (M>𝑴𝒃𝒂𝒍 )
@ Hoong-Pin Lee

70. Example 8
@ Hoong-Pin Lee

71. Example 8: Solution
@ Hoong-Pin Lee

72. Example 8: Solution
@ Hoong-Pin Lee

73. Example 8: Solution
@ Hoong-Pin Lee

74. Design Summary for Flanged
Beam
@ Hoong-Pin Lee

75. Design Summary for Flanged
Beam
@ Hoong-Pin Lee

76. End of Chapter 2
@ Hoong-Pin Lee